当前位置：首页 > news >正文

可持久化线段树系列题解

news 2025/8/4 7:24:59

我的题单

可持久化线段树

可持久化线段树，又称函数式线段树。通过保留每个版本的根，来保存线段树历史版本。

1.洛谷 P3919 可持久化线段树1

题意

如题，你需要维护这样的一个长度为 $N$ 的数组，支持如下两种操作：

在某个历史版本上修改某一个位置上的值。
访问某个历史版本上的某一位置的值。

此外，每进行一次操作，就会生成一个新的版本。版本编号即为当前操作的编号（从 $1$ 开始编号，版本 $0$ 表示初始状态数组）。

对于操作 $2$ ，即为生成一个完全一样的版本，不作任何改动。即，询问生成的版本是询问所访问的那个版本的复制。

$\leq N, M \leq {10}^6$ ， $\leq p \leq N$ 。设当前是第 $x$ 次操作， $\leq v < x$ ， $−109≤ai,c≤109-{10}^9 \leq a_i,c \leq {10}^9$ 。

思路

这是可持久化线段树的第一个经典应用，存放多个历史版本。

具体地，我们对于当前版本 $u$ 和前继版本 $p re$ ，我们用不同的树根 $r t$ （内存池）来区分不同版本，如果 $rt_u$ 还不存在就标记 $+ 1$ 新建。
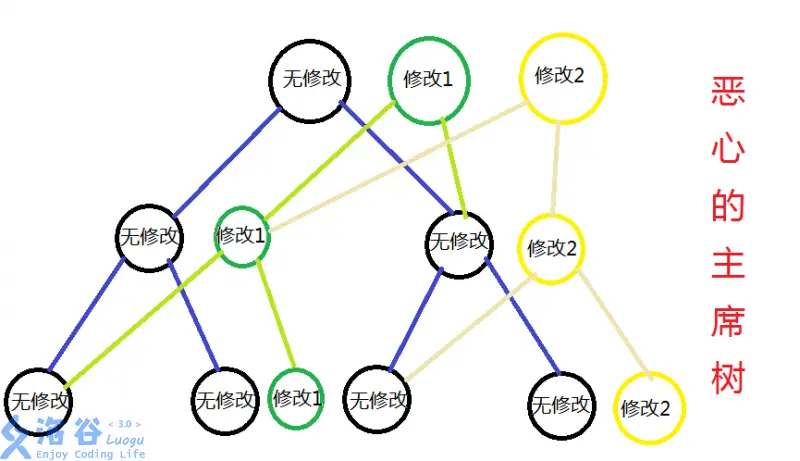
在这里插入图片描述
（图转自这篇博客）

在线段树上的结构体 node T[]，T[u] 先直接继承 T[pre]，然后在版本 $u$ 上更新。注意到每一次版本的复制，都只是继承 $p re$ 的基础上修改，有很多重复的点，因此在此每个节点的儿子不一定是 u<<1 和 u<<1|1，而是要特别记录 $l so n$ 和 $rso n$ 。

注意在这一题查询也算一个版本，对应着查询的版本编号，版本的直接继承，直接 $rt_i=rt_{pre}$ 即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e6+9;
ll n,m,a[N];
ll rt[N<<5];
struct Par_T
{ll cnt;struct node{ll ls,rs;ll val;}T[N<<5];void build(ll &u,ll l,ll r){u=++cnt;if(l==r){T[u].val=a[l];return;}ll mid=(l+r)>>1;build(T[u].ls,l,mid);build(T[u].rs,mid+1,r);}void modify(ll &u,ll pre,ll l,ll r,ll x,ll v)//历史状态 单点修改 {u=++cnt;T[u]=T[pre];if(l==r){T[u].val=v;return;}ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x,v);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x,v);}ll query(ll u,ll l,ll r,ll x){if(l==r)return T[u].val;ll mid=(l+r)>>1,ret=0;if(x<=mid)ret=query(T[u].ls,l,mid,x);if(x>mid)ret=query(T[u].rs,mid+1,r,x);return ret;}
}P;
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);P.build(rt[0],1,n);for(int i=1;i<=m;i++){ll pre,op,x,v;scanf("%lld%lld%lld",&pre,&op,&x);if(op==1){scanf("%lld",&v);P.modify(rt[i],rt[pre],1,n,x,v);}else {ll ans=P.query(rt[pre],1,n,x);printf("%lld\n",ans);rt[i]=rt[pre];}}return 0;
}

2.洛谷 P3834 可持久化线段树2 / nfls #2525 区间 k 大

题意

给定 $n$ 个整数构成的序列 $a$ ，将对于指定的闭区间 $[l, r]$ 查询其区间内的第 $k$ 小值。

$\leq n,m \leq 2\times 10^5$ ， $0≤ai≤1090\le a_i \leq 10^9$ ， $\leq l \leq r \leq n$ ， $\leq k \leq r - l + 1$ 。

思路

静态区间第 $k$ 小/大，是可持久化线段树的第二个经典应用。

先说 $[1, r]$ 的第 $k$ 小怎么做。考虑统计每个数 $a_i$ 的个数 $v a l$ ，按照 $i$ 个版本依次扔上可持久化线段树，主席树上节点 $v a l + 1$ （ $a_i$ 很大所以要离散化，之后的 $a_i$ 都是离散化过后的）。

像二叉查找树那样，反正也用了离散数组，对于查询排名 $k$ ，将左儿子节点个数 $x$ 与 $k$ 比较，如果 $k < x$ ，那么第 $k$ 小在左子树，否则在右子树。要注意，查询左子树的话递归时直接继承 $k$ ，查询右子树时需要减去“左子树的 $s i ze$ ”，也就是 $l∼midl\sim mid$ 元素个数的总和，即对于左右根 $u l, u r$ ，size=T[T[ur].ls].val-T[T[ul].ls].val，因为查询的是子树内的排名。

（大概是这样，图转自这篇题解）
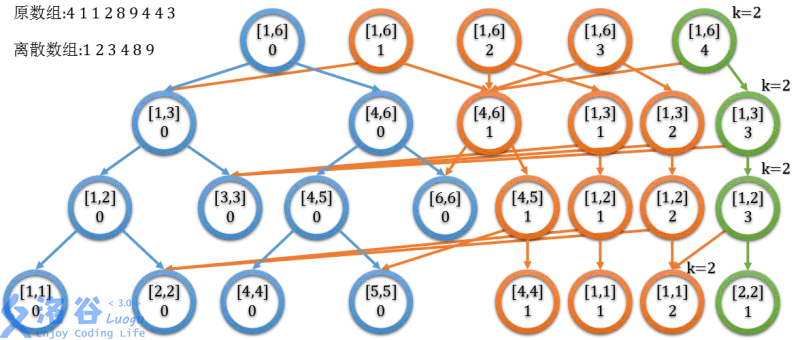
在这里插入图片描述
区间怎么办呢？如果我们可以得到，区间 $[l, r]$ 的每一个数的个数就好了，而可持久化线段树正好可以解决这样的问题：我们让版本 $r$ 的每一个节点减去版本 $l - 1$ 。也不需要单独拎出来减，一边递归一边减就好了。

维护的是桶，各个元素分离，也就没必要 pushup 了。

多个一样的数算一个名次，所以直接映射回去重后数组值即可。（原数组为 a[]，去重数组为 aa[]，lower_bound 时的 x 表示原 $a_i$ 离散化到名次）

具体细节见代码：

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9;
ll n,Q,a[N];
ll nn,aa[N];
ll rt[N];
struct ParT
{ll cnt;struct node{ll ls,rs;ll val;}T[N<<5];void build(ll &u,ll l,ll r){u=++cnt;if(l==r){T[u].val=0;return;}ll mid=(l+r)>>1;build(T[u].ls,l,mid);build(T[u].rs,mid+1,r);}void modify(ll &u,ll pre,ll l,ll r,ll x){u=++cnt;T[u]=T[pre];T[u].val++;if(l==r)return;ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x);}ll query(ll ul,ll ur,ll l,ll r,ll x){if(l==r)return aa[l];ll mid=(l+r)>>1,ret=0;ll rk=T[T[ur].ls].val-T[T[ul].ls].val;if(x<=rk)ret=query(T[ul].ls,T[ur].ls,l,mid,x);//左 if(x>rk)ret=query(T[ul].rs,T[ur].rs,mid+1,r,x-rk);return ret;}
}P;
int main()
{scanf("%lld%lld",&n,&Q);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);aa[i]=a[i];}sort(aa+1,aa+n+1);nn=unique(aa+1,aa+n+1)-aa-1;P.build(rt[0],1,nn);for(int i=1;i<=n;i++){ll x=lower_bound(aa+1,aa+nn+1,a[i])-aa;P.modify(rt[i],rt[i-1],1,nn,x);}while(Q--){ll l,r,x;scanf("%lld%lld%lld",&l,&r,&x);printf("%lld\n",P.query(rt[l-1],rt[r],1,nn,x));}return 0;
}

3.洛谷 P3939 数颜色

题意

小 C 的兔子不是雪白的，而是五彩缤纷的。每只兔子都有一种颜色，不同的兔子可能有相同的颜色。小 C 把她标号从 1 到 $n$ 的 $n$ 只兔子排成长长的一排，来给他们喂胡萝卜吃。排列完成后，第 $i$ 只兔子的颜色是 $a_i$ 。

俗话说得好，“萝卜青菜，各有所爱”。小 C 发现，不同颜色的兔子可能有对胡萝卜的不同偏好。比如，银色的兔子最喜欢吃金色的胡萝卜，金色的兔子更喜欢吃胡萝卜叶子，而绿色的兔子却喜欢吃酸一点的胡萝卜……为了满足兔子们的要求，小 C 十分苦恼。所以，为了使得胡萝卜喂得更加准确，小 C 想知道在区间 $l_j,r_j]$ 里有多少只颜色为 $a_j$ 的兔子。

不过，因为小 C 的兔子们都十分地活跃，它们不是很愿意待在一个固定的位置；与此同时，小 C 也在根据她知道的信息来给兔子们调整位置。所以，有时编号为 $x_j$ 和 $x_j+1$ 的两只兔子会交换位置。小 C 被这一系列麻烦事给难住了。你能帮帮她吗？

$1≤n≤3×1051\le n\le 3\times 10^5$ ， $1≤lj≤rj≤n1\le l_j\le r_j\le n$ ， $1≤xj≤n1\le x_j \le n$ ，操作 $1$ 和 $2$ 的次数均不超过 $3×1053\times 10^5$ 。

思路

对于操作 $1$ ，求区间颜色有几个，和 $2.$ 一样，直接版本 $r$ 减去版本 $l - 1$ 即可。

操作 $2$ 的话交换相邻元素位置。这一题维护的是 $1∼n1\sim n$ 不同版本的桶，每次新建一个版本都加入统计一个 $x_i$ 。交换 $a_x$ 和 $a_{x+1}$ ，版本 $x$ 的 $a_x$ 少了 $1$ ， $a_{x+1}$ 多了 $1$ ；而版本 $x + 1$ 的所有桶不变。

因此只需要修改版本 $x$ 。版本 $x$ 继承版本 $x - 1$ 之后在上面新加一个 $a_x'=a_{x+1}$ 即可。记得 swap(a[x],a[x+1])。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+9;
int n,Q,a[N];
int nn,aa[N],pos[N];
int rt[N];
struct ParT 
{int cnt;struct node{int ls,rs;int val;}T[N*40];void modify(int &u,int pre,int l,int r,int x){u=++cnt;T[u]=T[pre];T[u].val++;if(l==r)return;int mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x);}int query(int ul,int ur,int l,int r,int x){if(l==r)return T[ur].val-T[ul].val;int mid=(l+r)>>1,ret=0;if(x<=mid)ret=query(T[ul].ls,T[ur].ls,l,mid,x);if(x>mid)ret=query(T[ul].rs,T[ur].rs,mid+1,r,x);return ret;}
}P;
//可持久化权值线段树
int main()
{scanf("%d%d",&n,&Q);for(int i=1;i<=n;i++){scanf("%d",&a[i]);aa[i]=a[i];}sort(aa+1,aa+n+1);nn=unique(aa+1,aa+n+1)-aa-1;for(int i=1;i<=n;i++){int x=a[i];a[i]=lower_bound(aa+1,aa+nn+1,a[i])-aa;P.modify(rt[i],rt[i-1],1,nn,a[i]);pos[x]=a[i];}while(Q--){int op,l,r,x;scanf("%d",&op);if(op==1){scanf("%d%d%d",&l,&r,&x);if(pos[x])printf("%d\n",P.query(rt[l-1],rt[r],1,nn,pos[x]));else puts("0");}else {scanf("%d",&x);if(a[x]==a[x+1])continue;swap(a[x],a[x+1]);P.modify(rt[x],rt[x-1],1,nn,a[x]);}}return 0;
}

空间问题

由上面的几幅图可以看出，每次修改（重构）只会修改 $log⁡n\log n$ 个节点，因此复杂度可以保证。

而做可持久化线段树的题目，一个很烦的点就是空间到底要开多大？辛辛苦苦写的代码交上去喜提 RE（在 $9.$ 得到充分体现）。

关于主席树的空间：线段树本身要开 $4$ 倍空间，根据上文所讲，每次重构会修改 $log⁡n\log n$ 个节点，也就是新增了 $log⁡n\log n$ 个节点，那么空间按理来说要开 $4n+nlog⁡n4n+n\log n$ （重构量级为 $n$ ）。普遍的代码都是左移 $5$ 位，即 $×32\times 32$ 。

4.洛谷 P1383 高级打字机 / P6166 IOI2012 scrivener

题意

请为高级打字机设计一个程序，支持如下 $3$ 种操作：

T x：Type 操作，表示在文章末尾打下一个小写字母 $x$ 。
U x：Undo 操作，表示撤销最后的 $x$ 次修改操作。
Q x：Query 操作，表示询问当前文章中第 $x$ 个字母并输出。请注意 Query 操作并不算修改操作。

文章一开始可以视为空串。

$n≤105n\le 10^5$ 。

洛谷 P6166：输入的 P 改为 Q；询问操作下标从 1 开始。本题解将按照 P1383 数据范围讲解。

题意

加入操作就在上一个版本后面加入一个 $c$ 。因为是直接加所以不能用桶来统计，在节点修改字符值。

那怎么查询第 $x$ 个字母呢？因为字母无序所以要像 $2.$ 一样借鉴二叉查找树的结构：向下递归时如果左子树未满就先塞左子树，否则塞右子树。

那么我们要记录每个子树的 $s i z$ ，左子树满时有 $mi d - l + 1$ 个节点，当 $siz_{ls}<mid-l+1$ 就没满。

维护各子树 $s i z$ ，就要 pushup 了。查询的时候和 $2.$ 一样，左子树就直接递归，右子树记得先减去左子树的 $s i ze$ 再查询。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+9;
int n,Q,tick;
int rt[N<<5];
struct ParT
{int cnt;struct node{int ls,rs;int siz;char val;}T[N<<5];void pushup(int u){T[u].siz=T[T[u].ls].siz+T[T[u].rs].siz;}void modify(int &u,int pre,int l,int r,char c){u=++cnt;T[u]=T[pre];if(l==r){T[u].siz=1;T[u].val=c;return;}int mid=(l+r)>>1;if(T[T[u].ls].siz<mid-l+1)modify(T[u].ls,T[pre].ls,l,mid,c);//左子树未满 else modify(T[u].rs,T[pre].rs,mid+1,r,c);pushup(u); }char query(int u,int l,int r,int x){if(l==r)return T[u].val;int mid=(l+r)>>1;if(x<=T[T[u].ls].siz)return query(T[u].ls,l,mid,x);else return query(T[u].rs,mid+1,r,x-T[T[u].ls].siz);}
}P;
int main()
{scanf("%d",&Q);n=Q;while(Q--){char op,c;int x;cin>>op;if(op=='T'){cin>>c;tick++;P.modify(rt[tick],rt[tick-1],1,n,c);}if(op=='U'){scanf("%d",&x);tick++;rt[tick]=rt[tick-x-1];}if(op=='Q'){scanf("%d",&x);printf("%c\n",P.query(rt[tick],1,n,x));}}return 0;
}

5.洛谷 P3963 TJOI2013 奖学金

题意

小张学院有 $c$ 名学生，第 $i$ 名学生的成绩为 $a_i$ ，要获得的奖学金金额为 $b_i$ 。

要从这 $c$ 名学生中挑出 $n$ 名学生发奖学金。这个神秘人物爱好奇特，他希望得到奖学金的同学的成绩的中位数尽可能大，但同时，他们的奖学金总额不能超过 $f$ 。

$\leq n \leq 10^5$ ， $\leq c \leq 2 \times 10^5$ ， $\leq f \leq 2\times 10^9$ ， $\leq a_i \leq 2 \times 10^9$ ， $\leq b_i \leq 10^5$ 。

思路

选定人数 $n$ 保证为奇数，那么总有一个学生的成绩恰为中位数。令 $k=⌊n2⌋=(n+1)÷2k=\left \lfloor \dfrac{n}{2} \right \rfloor=(n+1)\div 2$ 。

我们考虑，贪心地按照学生的成绩从大到小枚举一个中位数，计算成绩 $1∼i1\sim i$ 的 $k$ 小的学生奖学金之和和 $i+1∼mi+1\sim m$ 的 $k$ 小的学生奖学金之和，相加判断是否超过额定数值。

像前面的题目一样，我们存区间的元素个数 $t o t$ ，在这里多维护一个区间的奖学金和 $s u m$ 。我们按照学生成绩从大到小插入可持久化线段树，这样保证了枚举的时候，前 $k$ 小 $>$ 枚举的中位数 $>$ 后 $k$ 小。

查询的时候，还是类似二叉查找树的结构，如果 $k≤sizlsk\le siz_{ls}$ ，就还能遍历左子树；否则要遍历右子树，在这里不仅 $k$ 要先减去 $siz_{ls}$ ，还要记得把左子树的 $s u m$ 算上，因为已经“遍历完了”。

具体细节见代码：

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9;
ll n,m,lim,k;
ll bb[N],nn;
struct stu
{ll scr,val;
}a[N];
ll rt[N],cnt;
bool cmp(stu x,stu y)
{return x.scr>y.scr;
}
struct ParT
{struct node{ll ls,rs;ll tot;//区间元素个数 ll sum;//奖学金总和 }T[N<<5];void build(ll &u,ll l,ll r){u=++cnt;if(l==r)return;ll mid=(l+r)>>1;build(T[u].ls,l,mid);build(T[u].rs,mid+1,r);}void modify(ll &u,ll pre,ll l,ll r,ll x){u=++cnt;T[u]=T[pre];T[u].tot++;T[u].sum+=bb[x];if(l==r)return;ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x);}ll query(ll ul,ll ur,ll l,ll r,ll k){if(l==r)return k*bb[l];//出现相同ll mid=(l+r)>>1,siz=T[T[ur].ls].tot-T[T[ul].ls].tot,ret=0;if(k<=siz)ret+=query(T[ul].ls,T[ur].ls,l,mid,k);else ret+=T[T[ur].ls].sum-T[T[ul].ls].sum+query(T[ul].rs,T[ur].rs,mid+1,r,k-siz);return ret;}
}P;
int main()
{scanf("%lld%lld%lld",&n,&m,&lim);k=n/2;for(int i=1;i<=m;i++){ll scr,val;scanf("%lld%lld",&scr,&val);a[i]=(stu){scr,val};bb[i]=val;}sort(a+1,a+m+1,cmp);sort(bb+1,bb+m+1);nn=unique(bb+1,bb+m+1)-bb-1;P.build(rt[0],1,nn);for(int i=1;i<=m;i++){ll pos=lower_bound(bb+1,bb+nn+1,a[i].val)-bb;P.modify(rt[i],rt[i-1],1,nn,pos);}for(int i=1+k;i<=m-k;i++)//枚举中位数 {ll le=P.query(rt[0],rt[i-1],1,nn,k);//前k=n/2小的和 ll ri=P.query(rt[i],rt[m],1,nn,k);//后k=n/2小 if(le+a[i].val+ri<=lim){printf("%lld",a[i].scr);return 0;}}puts("-1");return 0;
}

6.洛谷 P3567 POI2014 KUR-Couriers / P7252 JSOI2011 棒棒糖

题意

给一个长度为 $n$ 的正整数序列 $a$ 。共有 $m$ 组询问，每次询问一个区间 $[l, r]$ ，是否存在一个数在 $[l, r]$ 中出现的次数严格大于一半。如果存在，输出这个数，否则输出 $0$ 。

$1≤n,m≤5×10^5$ ， $1≤ai≤n1\le a_i\le n$ 。

洛谷 P7257：本体弱化版， $n$ 为当前 $110\frac{1}{10}$ 。本题解将按照 P3567 数据范围讲解。

思路

依然是版本 $1∼n1\sim n$ 依次在可持久化线段树加入 $a_i$ ，维护一个桶，查询 $[l, r]$ 时，版本 $r$ 减去版本 $l - 1$ 。如果大于等于 $l$ 小于等于 $mi d$ 的数字的数量超过 $r−l+12\dfrac{r-l+1}{2}$ 就往左子树下查询，大于等于 $mi d + 1$ 小于等于 $r$ 的数字的数量超过 $r−l+12\dfrac{r-l+1}{2}$ 就往右子树下查询，都没有就返回 $0$ 。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5e5+9;
ll n,Q,a[N];
ll nn,aa[N];
ll rt[N];
struct ParT
{ll cnt;struct node{ll ls,rs;ll val;}T[N<<5];void modify(ll &u,ll pre,ll l,ll r,ll x){u=++cnt;T[u]=T[pre];T[u].val++;if(l==r)return;ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x);}ll query(ll ul,ll ur,ll l,ll r,ll tot){if(l==r)return aa[l];ll mid=(l+r)>>1;ll l_mid=T[T[ur].ls].val-T[T[ul].ls].val;ll mid_r=T[T[ur].rs].val-T[T[ul].rs].val;if(tot<l_mid)return query(T[ul].ls,T[ur].ls,l,mid,tot);if(tot<mid_r)return query(T[ul].rs,T[ur].rs,mid+1,r,tot);return 0;}
}P;
int main()
{scanf("%lld%lld",&n,&Q);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);aa[i]=a[i];}sort(aa+1,aa+n+1);nn=unique(aa+1,aa+n+1)-aa-1;for(int i=1;i<=n;i++){ll x=lower_bound(aa+1,aa+nn+1,a[i])-aa;P.modify(rt[i],rt[i-1],1,nn,x);}while(Q--){ll l,r;scanf("%lld%lld",&l,&r);ll mid=(r-l+1)>>1;printf("%lld\n",P.query(rt[l-1],rt[r],1,nn,mid));}return 0;
}

7.洛谷 P6592 幼儿园

题意

Ysuperman 热爱在 TA 的幼儿园里散步，为了更方便散步， TA 把幼儿园抽象成 $n$ 个点， $m$ 条边的有向图。散步得多了， TA 就给了每一条边无与伦比的亲密程度： $1,2,⋯,m1,2,\cdots,m$ ，越大代表越亲密。 TA 也给了每一个点无与伦比的编号： $1,2,⋯,n1,2,\cdots,n$ ，其中 $1$ 代表着幼儿园大门，但是每个点是没有亲密程度的。

接下来 $k$ 天，Ysuperman 每天会有一次散步计划。具体而言， TA 希望从 $x_i$ 号点出发，只经过亲密程度属于区间 $l_i,r_i]$ 的边，走到幼儿园大门 $1$ 号点，期间经过的边的亲密程度必须单调递减，不然会因为 TA 有强迫症而不能回家。

具体而言，对于每一天的计划，如果可行，则输出 1，反之输出 0。

当然啦，有的时候 Ysuperman 很着急，需要你立马回复，有的时候 TA 可以等等你，先把所有问题问完再等你回复。（即可以离线）

$\le n \le 10^5 ,1 \le m,k \le 2\times10^5$ ， $w∈{0,1}w\in\{0,1\}$ ， $\le u_i,v_i \le n$ 。 $x_i,l_i,r_i$ 在解密后保证 $1≤x≤n,1≤li,ri≤m1\le x \le n ,1 \le l_i,r_i \le m$ 。不保证不出现重边自环，不保证图联通。

思路

这题有个奇怪的条件：走过的边必须单调递减。

我们不妨先想一下离线怎么做。我们发现给定的区间 $[l, r]$ 相当于限定了多少边；如果我们从 $1$ 开始到 $n$ 逐次打开编号为 $i$ 的边（即枚举每个 $r$ ），对于每个边 $ui→viu_i\to v_i$ ， $u_i$ 走到 $1$ 途中经过的边权的最小值可能会改变，而我们期望 $r$ 一定时，这个最小值最大。

那么有转移：
$f_{u_i}=\max\{min(f_v,i)\}$

初始化 $f1=inff_1=\text{inf}$ 。

我们设 $f_i$ 表示 $i$ 开始走到 $1$ 途中经过的边权的最小值的最大可能。对于不同的最大值 $r$ ，因为打开的边不同，对应的 $f_i$ 不同，而且要求走过的编号单调递减，我们考虑从小到大枚举边的编号 $i∈[1,m]i\in[1,m]$ 作为一次行走的最大值，每次开一个版本 $i$ ，存放 $fui←min⁡(i,fv)f_{u_i}\leftarrow \min(i,f_v)$ 。这样子，没有枚举到的边就走不了，保证了走的边是单调递减的。

查询的时候，对于询问的最大值 $r$ ，查询历史版本 $r$ 的对应 $f_x$ ，查询下界是否大于等于 $l$ 即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9,inf=0x3f3f3f3f;
ll n,m,Q,w;
struct bian
{ll u,v,w;
}b[N];
ll rt[N];
ll f[N];//从i走到1经过递减边权的最小值的最大可能 
struct ParT
{ll cnt;struct node{ll ls,rs;ll val;}T[N<<5];void build(ll &u,ll l,ll r){u=++cnt;if(l==r){T[u].val=f[l];return; }ll mid=(l+r)>>1;build(T[u].ls,l,mid);build(T[u].rs,mid+1,r);}void modify(ll &u,ll pre,ll l,ll r,ll x,ll v){u=++cnt;T[u]=T[pre];if(l==r){T[u].val=v;return;}ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x,v);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x,v);}ll query(ll u,ll l,ll r,ll x){if(l==r)return T[u].val;ll mid=(l+r)>>1,ret=0;if(x<=mid)ret=query(T[u].ls,l,mid,x);if(x>mid)ret=query(T[u].rs,mid+1,r,x);return ret;}
}P;
int main()
{scanf("%lld%lld%lld%lld",&n,&m,&Q,&w);for(int i=1;i<=m;i++){ll u,v;scanf("%lld%lld",&u,&v);b[i]=(bian){u,v,i};}f[1]=inf;for(int i=2;i<=n;i++)f[i]=-inf;P.build(rt[0],1,n);for(ll i=1;i<=m;i++){ll u=b[i].u,v=b[i].v;f[u]=max(f[u],min(i,f[v]));//最小边权的最大值P.modify(rt[i],rt[i-1],1,n,u,f[u]);}ll sans=0;while(Q--){ll x,l,r;scanf("%lld%lld%lld",&x,&l,&r);if(w)x^=sans,l^=sans,r^=sans;ll r_fx=P.query(rt[r],1,n,x),ans=(r_fx>=l);printf("%lld\n",ans);sans+=ans;}return 0;
}

8.洛谷 P2617 Dynamic Rankings

题意

给定一个含有 $n$ 个数的序列 $a1,a2…ana_1,a_2 \dots a_n$ ，需要支持两种操作：

Q l r k 表示查询下标在区间 $[l, r]$ 中的第 $k$ 小的数
C x y 表示将 $a_x$ 改为 $y$

$1≤n,m≤1051\le n,m \le 10^5$ ， $\le l \le r \le n$ ， $\le k \le r-l+1$ ， $1≤x≤n1\le x \le n$ ， $\le a_i,y \le 10^9$ 。

思路

第一反应我们想用可持久化线段树，因为这是解决静态区间第 $k$ 小的经典算法。但是这里需要修改，如果一个一个根修改每次 $Θ(log⁡n)\Theta(\log n)$ ，最劣要去到 $Θ(mnlog⁡n)\Theta(mn\log n)$ ，显然不行。

可持久化线段树求区间 $k$ 小的原理，是保存 $1∼n1\sim n$ 的每次加 $a_i$ 的历史版本，对于 $[l, r]$ ，我们用版本 $r$ 减去版本 $l - 1$ ，看看左树 $l s i ze$ 和 $k$ 的大小关系，来决定遍历 $[l, mi d]$ 还是 $[mi d + 1, r]$ 。这是一种前缀和的思想。

既然是前缀和的思想，那么我们在修改的时候，当然可以用树状数组优化，从 $x$ 到 $n$ 每次跳 $lowbit\text{lowbit}$ 。这样我们做到了单次 $Θ(log⁡2n)\Theta(\log^2 n)$ 修改。

void Modify(int x,int v)
{int pos=lower_bound(aa+1,aa+nn+1,a[x])-aa;//离散化for(int i=x;i<=n;i+=lowbit(i))modify(rt[i],1,nn,pos,v);//可持久化权值线段树
}

至于查询操作，我们就用如上的前缀和优化的思想，对于 $r$ 和 $l - 1$ 我们跳 $lowbit\text{lowbit}$ 把对应的历史版本的 $r t$ 记下来，像普通可持久化线段树一样算左子树 $l s i z$ （根f的左儿子相减），和 $k$ 比大小决定遍历左区间还是右区间。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9,M=2e5+9;
ll n,m,a[N];
ll nn,aa[M];
struct que
{char op;ll l,r,k;
}q[N];
ll rt[N];
ll r1[N],r2[N],tot1,tot2; 
ll cnt;
struct node
{ll ls,rs;ll val;
}T[N*400];
void modify(ll &u,ll l,ll r,ll x,ll v)
{if(!u)u=++cnt;T[u].val+=v;if(l==r)return;ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,l,mid,x,v);if(x>mid)modify(T[u].rs,mid+1,r,x,v);
}
ll lowbit(ll x)
{return x&(-x);
}
void Modify(ll x,ll v)
{ll pos=lower_bound(aa+1,aa+nn+1,a[x])-aa;for(int i=x;i<=n;i+=lowbit(i))modify(rt[i],1,nn,pos,v);
}
ll query(ll l,ll r,ll k)
{if(l==r)return l;ll siz=0;for(int i=1;i<=tot1;i++)siz-=T[T[r1[i]].ls].val;for(int i=1;i<=tot2;i++)siz+=T[T[r2[i]].ls].val;ll mid=(l+r)>>1;if(k<=siz){for(int i=1;i<=tot1;i++)r1[i]=T[r1[i]].ls;for(int i=1;i<=tot2;i++)r2[i]=T[r2[i]].ls;return query(l,mid,k);}else {for(int i=1;i<=tot1;i++)r1[i]=T[r1[i]].rs;for(int i=1;i<=tot2;i++)r2[i]=T[r2[i]].rs;return query(mid+1,r,k-siz);}
}
ll Query(ll l,ll r,ll k)
{tot1=tot2=0;for(int i=l-1;i>=1;i-=lowbit(i))r1[++tot1]=rt[i];for(int i=r;i>=1;i-=lowbit(i))r2[++tot2]=rt[i];return query(1,nn,k);
}
int main()
{scanf("%lld%lld",&n,&m);ll tot=0;for(int i=1;i<=n;i++){scanf("%lld",&a[i]);aa[++tot]=a[i];}for(int i=1;i<=m;i++){char op;ll x,y,k=0;cin>>op;scanf("%lld%lld",&x,&y);if(op=='Q')scanf("%lld",&k);else aa[++tot]=y;q[i]=(que){op,x,y,k};}sort(aa+1,aa+tot+1);nn=unique(aa+1,aa+tot+1)-aa-1;for(int i=1;i<=n;i++)Modify(i,1);for(int i=1;i<=m;i++){if(q[i].op=='Q')printf("%lld\n",aa[Query(q[i].l,q[i].r,q[i].k)]);else {Modify(q[i].l,-1);a[q[i].l]=q[i].r;Modify(q[i].l,1);}}return 0;
}

9.洛谷 P3302 SDOI2013 森林 / P2633 Count on a tree

题意

小 Z 有一片森林，含有 $N$ 个节点，每个节点上都有一个非负整数作为权值。初始的时候，森林中有 $M$ 条边。

小Z希望执行 $T$ 个操作，操作有两类：

Q x y k 查询点 $x$ 到点 $y$ 路径上所有的权值中，第 $k$ 小的权值是多少。此操作保证点 $x$ 和点 $y$ 连通，同时这两个节点的路径上至少有 $k$ 个点。
L x y 在点 $x$ 和点 $y$ 之间连接一条边。保证完成此操作后，仍然是一片森林。

为了体现程序的在线性，我们把输入数据进行了加密。设 $l a s t an s$ 为程序上一次输出的结果，初始的时候 $l a s t an s$ 为 $0$ 。

对于一个输入的操作 Q x y k，其真实操作为 Q x^lastans y^lastans k^lastans。

对于一个输入的操作 L x y，其真实操作为 L x^lastans y^lastans。

所有节点的编号在 $1∼N1\sim N$ 的范围内，节点上的权值 $≤109\le 10^9$ 。 $M < N$ 。

洛谷 P2633：只有询问操作没有连边。本题解将按照 P3302 数据范围讲解。

思路

不会写 LCT 就用可持久化线段树。

节点权值范围较大，因此离散化。因为查询的时路径上各权值的第 $k$ 小，刚好可持久化线段树有着存储历史版本、历史版本相减的特点，可以利用 $u, v, l c a (u, v)$ 版本相减来获取路径。

于是考虑在建边过程中，版本 $u$ 在版本 $fa_u$ 的基础上，添加（去重离散化后）权值 $t_u$ 。

P.modify(rt[u],rt[fa],1,nn,t[u]);

对于查询操作，因为版本 $u$ 和版本 $v$ 并无关联，而能够联系二者的有 $l c a (u, v)$ 。因此我们考虑把 $u→vu\rightarrow v$ 的路径拆成如图所示：
在这里插入图片描述
具体地，我们分成两段来 qurey，版本 $u$ 减去版本 $2$ ，即 $fa_{lca}=$ f[LCA][0]；版本 $v$ 减去版本 $l c a$ 。这时在可持久化线段树上左子树由两端组成：

P.query(rt[f[LCA][0]],rt[LCA],rt[u],rt[v],1,nn,k);
...
siz1+siz2=T[T[ur1].ls].siz-T[T[ul1].ls].siz+T[T[ur2].ls].siz-T[T[ul2].ls].siz

此时再二叉查找，判断 $k$ 是否大于 $s i z 1 + s i z 2$ ，如果小于就一起遍历两段的左子树，否则就 $k - s i z 1 - s i z 2$ ，一起遍历右子树。

还有个合并操作，直接连边，然后暴力 dfs 更新 lca 所需的 $f$ 倍增数组。但是谁做谁的父亲呢？这时候想到启发式合并：我们把 $s i z$ 小的作为儿子， $s i z$ 大的作为父亲，显然比反过来减少了很多冗余路径，使得更新次数更少，这样合并使复杂度从 $O (n)$ 优化到 $O(log⁡n)O(\log n)$ 。（关于按秩合并、启发式合并的说明）

当你兴冲冲交了一发，发现 70pts，RE 了 $3$ 个点，原因是空间没开够和 lca 上界的问题。

首先空间，因为操作 $T$ 次（和 $n$ 同阶）启发式合并保证了约莫 $O(log⁡n)O(\log n)$ 的复杂度，意味着暴力用 dfs 更新大概需要 $log⁡n\log n$ 次；而每次 dfs 更新一条边跑一边可持久化线段树的 modify，重构次数大概 $log⁡n\log n$ 次。再加上原始 $4$ 倍空间和初始建 $m$ 条边的 $log⁡n\log n$ 次新建节点，空间复杂度是 $O(n(4+\log n+\log^2n))$ ，开 $300$ 多足以应对。

然后是lca 的上界，详参这篇博客。上界太低会导致暴力更新的时候无法向上继续跳；在求 lca 时， $x, y$ 一起向上倍增跳就会出错，访问到很大的数导致 RE。就不能只是 (1<<i)<=dep[u]，要去到 $⌈log⁡n⌉\left\lceil \log n \right\rceil$ ，大概 $17∼1917\sim 19$ 。

具体细节见代码：

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=8e4+9;
ll id,n,m,Q;
ll a[N];
ll aa[N],nn,t[N];//离散化数组 
ll rt[N],cnt;
struct ParT
{struct node{ll siz;ll ls,rs;}T[N*320];//4+log^2void build(ll &u,ll l,ll r){u=++cnt;if(l==r)return;ll mid=(l+r)>>1;build(T[u].ls,l,mid);build(T[u].rs,mid+1,r);}void modify(ll &u,ll pre,ll l,ll r,ll x){u=++cnt;T[u]=T[pre];T[u].siz++;if(l==r)return;ll mid=(l+r)>>1;if(x<=mid)modify(T[u].ls,T[pre].ls,l,mid,x);if(x>mid)modify(T[u].rs,T[pre].rs,mid+1,r,x);}ll query(ll ul1,ll ul2,ll ur1,ll ur2,ll l,ll r,ll k){if(l==r)return aa[l];ll siz1=T[T[ur1].ls].siz-T[T[ul1].ls].siz;ll siz2=T[T[ur2].ls].siz-T[T[ul2].ls].siz;ll mid=(l+r)>>1,ret=0;if(k<=siz1+siz2)ret=query(T[ul1].ls,T[ul2].ls,T[ur1].ls,T[ur2].ls,l,mid,k);else ret=query(T[ul1].rs,T[ul2].rs,T[ur1].rs,T[ur2].rs,mid+1,r,k-siz1-siz2);return ret;}
}P;
struct edge
{ll to,next;
}e[N<<2];//(M+Q)*2
ll idx,head[N];
void addedge(ll u,ll v)
{idx++;e[idx].to=v;e[idx].next=head[u];head[u]=idx;
}
ll Fa[N];
ll fz(ll x)
{while(x!=Fa[x])x=Fa[x]=Fa[Fa[x]];return x;
}
ll dep[N],f[N][19];
ll siz[N];
bool vis[N];
void dfs(ll u,ll fa,ll root)
{vis[u]=1;dep[u]=dep[fa]+1;f[u][0]=Fa[u]=fa;for(int i=1;i<=18;i++)//上界(1<<i)<=dep[u]可能过小 f[u][i]=f[f[u][i-1]][i-1];P.modify(rt[u],rt[fa],1,nn,t[u]);siz[root]++;//用来按秩合并 for(int i=head[u];i;i=e[i].next){ll v=e[i].to;if(v==fa)continue;dfs(v,u,root);}
}
ll lca(ll x,ll y)
{if(dep[x]<dep[y])swap(x,y);for(int i=18;i>=0;i--)if(dep[x]-(1<<i)>=dep[y])x=f[x][i];if(x==y)return x;for(int i=18;i>=0;i--){if(f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}
void join(ll u,ll v)//按秩合并 
{addedge(u,v);addedge(v,u);ll fu=fz(u),fv=fz(v);if(siz[fu]>siz[fv])dfs(v,u,fu);else dfs(u,v,fv);
}
int main()
{scanf("%lld",&id);scanf("%lld%lld%lld",&n,&m,&Q);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);aa[i]=a[i];}sort(aa+1,aa+n+1);nn=unique(aa+1,aa+n+1)-aa-1;P.build(rt[0],1,nn);for(int i=1;i<=n;i++)t[i]=lower_bound(aa+1,aa+nn+1,a[i])-aa;for(int i=1;i<=m;i++){ll u,v;scanf("%lld%lld",&u,&v);addedge(u,v);addedge(v,u);}for(int i=1;i<=n;i++){if(!vis[i]){dfs(i,0,i);Fa[i]=i;}}ll lans=0;while(Q--){char op;ll u,v,k;cin>>op;scanf("%lld%lld",&u,&v);u^=lans,v^=lans;if(op=='Q'){scanf("%lld",&k);k^=lans;ll LCA=lca(u,v);lans=P.query(rt[f[LCA][0]],rt[LCA],rt[u],rt[v],1,nn,k);printf("%lld\n",lans);//不能用并查集的 Fa }else join(u,v);}return 0;
}