当前位置：首页 > news >正文

Back to the Features中，直观物理的评价指标是什么，计算方式是什么

news 2025/8/4 6:44:43

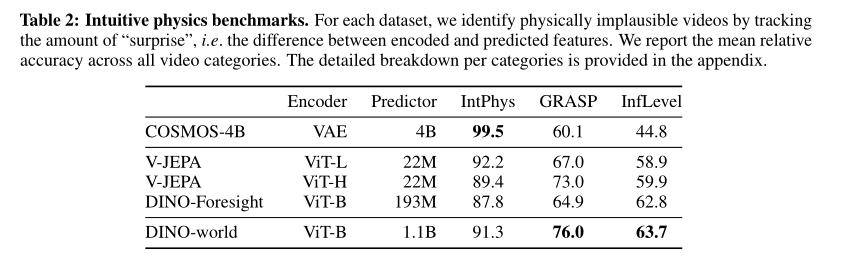
在这里插入图片描述
这张表（Table 2: Intuitive physics benchmarks）中用到的评价指标是意外程度的度量。
our world model,V-JEPA, and DINO-Foresight都是使用预测特征与实际特征之间的平均绝对误差作为意外程度的度量,COSMOS使用自回归预测器在预测离散潜在标记时的困惑度。

COSMOS指标（困惑度）的计算方式

困惑度（Perplexity）是衡量语言模型或自回归模型预测能力的一个常用指标，在COSMOS模型中，用于衡量自回归预测器在预测离散潜在标记时的表现，其计算过程如下：

基本概念：在自回归模型中，模型会根据之前已经生成的序列来预测下一个元素。对于离散潜在标记的预测，模型会输出每个可能标记的概率分布。
计算公式：假设离散潜在标记的序列为 $(x1,x2,…,xn(x_1, x_2, \ldots, x_n$ )，模型在预测每个标记 $x_i$ ) 时，基于前面 $(i - 1$ ) 个标记给出的概率分布为 $(P(xi∣x1,…,xi−1)(P(x_i | x_1, \ldots, x_{i - 1})$ )。困惑度的计算公式为：
$2^{-\frac{1}{n}\sum_{i = 1}^{n}\log_2 P(x_i | x_1, \ldots, x_{i - 1})}$
其中， $(log⁡2P(xi∣x1,…,xi−1)(\log_2 P(x_i | x_1, \ldots, x_{i - 1})$ ) 表示模型对真实标记 $x_i$ ) 预测的对数概率， $(1n∑i=1nlog⁡2P(xi∣x1,…,xi−1)(\frac{1}{n}\sum_{i = 1}^{n}\log_2 P(x_i | x_1, \ldots, x_{i - 1})$ ) 是平均对数概率。困惑度可以理解为模型对下一个标记预测的不确定性程度，困惑度越低，说明模型对数据的预测越准确，不确定性越小。

不同度量定义能否一起比较

虽然V - JEPA、DINO - Foresight使用预测特征与实际特征之间的平均绝对误差（MAE），而COSMOS使用困惑度作为指标，但它们在一定程度上是可以一起比较的，原因如下：

共同目标：这些指标都是为了衡量模型在预测任务中的性能。无论是平均绝对误差还是困惑度，本质上都是对模型预测结果与真实情况之间差异的一种量化。它们都反映了模型对数据的学习和预测能力，从这个角度看，具有可比性基础。
相对性能评估：在比较不同模型时，我们更关注的是模型之间的相对性能。例如，在相同的实验设置和数据集下，如果一个模型的平均绝对误差明显低于其他模型，或者其困惑度更低，我们可以认为该模型在预测任务中表现更好。即使指标的计算方式不同，但通过相对数值的比较，依然能够判断出哪个模型在整体性能上更优。

然而，也存在一些限制使得直接比较可能不够精确：

指标性质差异：平均绝对误差是基于连续特征之间的差异计算，而困惑度是针对离散潜在标记的概率预测。两者在数值范围和物理意义上有所不同，这可能导致在绝对数值上的比较缺乏直观性。
任务侧重点不同：不同的指标可能反映了模型在不同方面的性能。平均绝对误差更关注特征层面的精确匹配，而困惑度更侧重于模型对离散标记序列的预测能力。因此，仅依靠单一指标的比较可能无法全面反映模型在所有任务上的表现。

为了更准确地进行比较，可以采取以下措施：