当前位置： 首页 > news >正文

动态规划精讲：01背包问题的理论、优化与三大经典变种应用

news 2025/8/4 6:21:09

49.01背包

01背包
描述
你有一个背包，最多能容纳的体积是V。

现在有n个物品，第i个物品的体积为vi ,价值为wi​。

（1）求这个背包至多能装多大价值的物品？

（2）若背包恰好装满，求至多能装多大价值的物品？
输入描述
第一行两个整数n和V，表示物品个数和背包体积。

接下来n行，每行两个数vi和wi​，表示第i个物品的体积和价值。
1≤n,V,vi​,wi​≤1000
输出描述
输出有两行，第一行输出第一问的答案，第二行输出第二问的答案，如果无解请输出0。

示例一

输入：3 5
2 10
4 5
1 4
输出：14
9
说明：装第一个和第三个物品时总价值最大，但是装第二个和第三个物品可以使得背包恰好装满且总价值最大。

示例二

输入：3 8
12 6
11 8
6 8
输出：8
0
说明：装第三个物品时总价值最大但是不满，装满背包无解。

根据最后一个位置定义状态表示
dp[i] [j]表示：从前i个物品中选，总体积不超过j，所有选法中，能挑选出来的最大价值

如果我们不挑选i位置的物品，我们从i-1位置之前去挑，并且总体积不超过j

如果我们选择i位置的物品，那么就肯定有w[i]，那么我们接下来去(0,i-1)挑个最大的价值就行了，我们在i位置挑选物品的时候，总体积不能超过j
但是在i-1之前挑选物品的时候，总体积不能超过j-v[i]

我们在选i号物品的时候，里面的内容移动要j-v[i]>=0
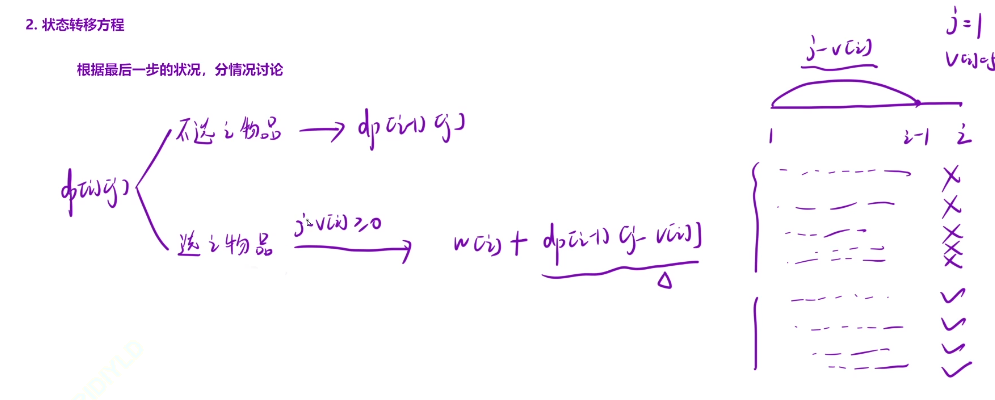
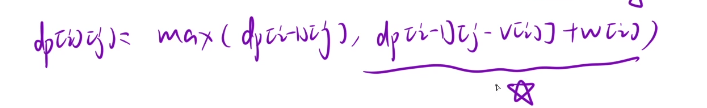
image.png
image.png

我们扩了一行一列，都初始化为0就行了

这个是处理第一题的，求这个背包至多能装多大价值的物品

第二问的是若背包恰好装满，求至多能装多大价值的物品？
那么我们就这么进行表示
dp[i] [j]表示：从前i个物品中挑选，总体积正好等于j，所有选法中，能挑选出来的最大价值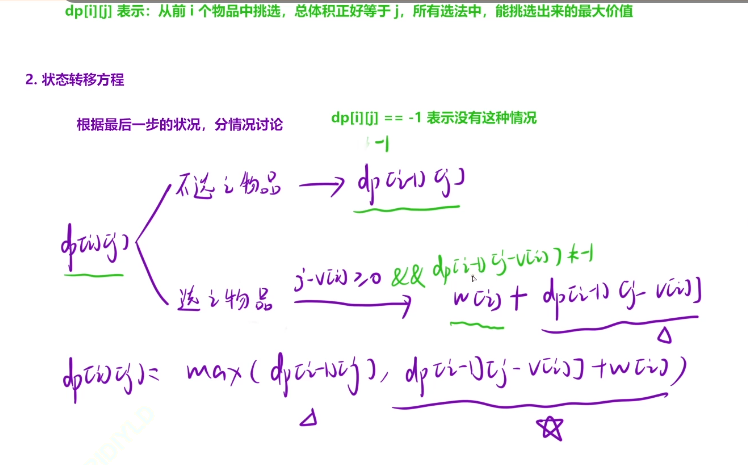image.png

初始化
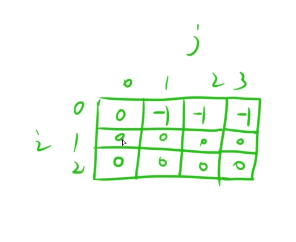
image.png

#include <iostream>#include<string.h>using namespace std;const int N=1010;int n,V,v[N],w[N];int dp[N][N];//默认初始化为0int main(){//读入数据cin>>n>>V;//循环输入数据到数组中去for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}//解决第一问for(int i=1;i<=n;i++){for(int j=1;j<=V;j++)//j表示的是容量，不能超过j{dp[i][j]=dp[i-1][j];//这种就是不选i位置的，去i-1位置选价值不超过j的//在我们选择i位置之后，还有j还有剩余的，那么我们就去i-1位置去选j-v[i]价值的if(j-v[i]>=0)dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);//这里最后记得加上w[i]的价值}}cout<<dp[n][V]<<endl;//解决第二问memset(dp,0,sizeof dp);//将dp表全部清空为0//-1的这种状态表示的是你想正好凑成价格为j是不存在的for(int j=1;j<=V;j++)dp[0][j]=-1;//在第一行位置，从1开始，都初始化为-1for(int i=1;i<=n;i++){for(int j=1;j<=V;j++)//j表示的是容量，不能超过j{dp[i][j]=dp[i-1][j];//这种就是不选i位置的，去i-1位置选价值不超过j的//在我们选择i位置之后，还有j还有剩余的，那么我们就去i-1位置去选j-v[i]价值的//我们这里一定要判断dp[j-v[i]]!=-1,就算说我们是能凑成j-v[i]这个体积的if(j-v[i]>=0&&dp[i-1][j-v[i]]!=-1)dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);//这里最后记得加上w[i]的价值}}cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;//如果这里面的是值-1的话，那么我们就输入0就行了，如果不是-1的话，那么我我们就输出这个值就行了return 0;}

为什么初始化为-1

  • 在动态规划的初始状态中，dp[i][j] 通常表示前 i 个物品能装进容量为 j 的背包的最大价值。默认情况下，如果某个背包容量 j 无法通过选择前 i 个物品填满，dp[i][j] 就是 0（代表未选物品）。

  • 但是，在第二问中，我们要标记那些无法通过物品恰好填满背包的容量。通过设置 -1，我们可以区分“不可达的状态”和“可以填满的状态”。

但是我们初始化为-1的仅仅是第一行啊，怎么影响到其他行呢
非常好的问题！你提到了初始化为 -1 仅仅是在 第一行，而你关心的是它如何影响到其他行。

这里的关键是 状态转移 和 动态规划的过程。虽然我们在初始化时将第一行的 dp[0][j] 设置为 -1，这并不会直接影响后续行的初始化。关键在于 如何通过状态转移，逐步地更新动态规划表中的值。

状态转移的核心思想

  1. 第一行初始化：我们设定 dp[0][j] = -1，表示没有物品时无法填满任何容量的背包。这个 -1 只会影响到第一行，因为在第一行时，我们没有物品可以选择。

  2. 后续行的状态转移：后面的 dp[i][j] 是通过前面行的数据进行推算的。每一行的计算是基于前一行的状态转移来的。特别地，当我们计算 dp[i][j] 时，依赖于前一行的 dp[i-1][j-v[i]]，这就是动态规划的核心：逐步计算并更新每一行的值。

详细分析

  1. 初始化第一行：

    • 第一行表示没有物品，所有容量 j 都初始化为 -1，表示无法填满。

  2. 第二行及之后的行：

    • 对于每一行（即每一个物品），我们会根据前一行（即前 i-1 个物品）的值来计算当前行（即前 i 个物品）能填满的背包容量。

    • 如果 dp[i-1][j-v[i]] != -1，说明前 i-1 个物品能够凑出容量为 j-v[i] 的背包，这时就可以选择当前物品 i，并更新当前背包的最大价值。

    • 即使 dp[i-1][j-v[i]] 是 -1（表示无法凑出容量 j-v[i]），在计算时就不会更新当前 dp[i][j]。

举个例子

假设有 3 个物品，背包容量是 7。

物品信息：

  • 物品 1：体积 3，价值 4

  • 物品 2：体积 4，价值 5

  • 物品 3：体积 5，价值 6

我们要求的是是否能够恰好填满容量为 7 的背包，且求最大价值。

初始化第一行

首先，我们初始化 dp[0][j] 为 -1，即表示没有物品时无法填满任何背包容量。

dp[0][0] = 0
dp[0][1] = -1
dp[0][2] = -1
dp[0][3] = -1
dp[0][4] = -1
dp[0][5] = -1
dp[0][6] = -1
dp[0][7] = -1

处理第一个物品（体积 3，价值 4）

我们在处理第一个物品时，基于 dp[0][j] 的值进行更新。我们检查每一个容量 j 是否可以通过选择物品 1 来填满背包。

  • 对于 j = 3，我们有 dp[0][3-3] != -1（dp[0][0] = 0），因此可以通过选择物品 1 来填满容量为 3 的背包，更新 dp[1][3] = 4。
dp[1][0] = 0
dp[1][1] = -1
dp[1][2] = -1
dp[1][3] = 4  // 选择物品 1
dp[1][4] = -1
dp[1][5] = -1
dp[1][6] = -1
dp[1][7] = -1

处理第二个物品（体积 4，价值 5）

接着，我们处理第二个物品，继续基于前一行（dp[1][j]）的值更新当前行（dp[2][j]）。检查是否可以通过选择物品 2 来填满背包。

  • 对于 j = 4，我们有 dp[1][4-4] != -1（dp[1][0] = 0），因此可以选择物品 2 来填满容量为 4 的背包，更新 dp[2][4] = 5。

  • 对于 j = 7，我们有 dp[1][7-4] != -1（dp[1][3] = 4），因此可以选择物品 2 来填满容量为 7 的背包，更新 dp[2][7] = 9。

dp[2][0] = 0
dp[2][1] = -1
dp[2][2] = -1
dp[2][3] = 4
dp[2][4] = 5  // 选择物品 2
dp[2][5] = -1
dp[2][6] = -1
dp[2][7] = 9  // 选择物品 2 + 物品 1

处理第三个物品（体积 5，价值 6）

最后，我们处理第三个物品，继续基于前一行（dp[2][j]）的值更新当前行（dp[3][j]）。检查是否可以通过选择物品 3 来填满背包。

  • 对于 j = 5，我们有 dp[2][5-5] != -1（dp[2][0] = 0），因此可以选择物品 3 来填满容量为 5 的背包，更新 dp[3][5] = 6。

  • 对于 j = 7，我们有 dp[2][7-5] != -1（dp[2][2] = -1），所以不能通过物品 3 填满容量为 7 的背包。

dp[3][0] = 0
dp[3][1] = -1
dp[3][2] = -1
dp[3][3] = 4
dp[3][4] = 5
dp[3][5] = 6  // 选择物品 3
dp[3][6] = -1
dp[3][7] = 9  // 选择物品 2 + 物品 1

结果

最终，dp[3][7] = 9，表示我们可以恰好填满容量为 7 的背包，最大价值是 9。

总结

  • 状态转移：每一行的计算是基于上一行的计算结果。dp[i][j] 会依赖于 dp[i-1][j-v[i]]，即前 i-1 个物品是否能够凑出容量 j-v[i]。

  • 影响传播：虽然 -1 是在第一行初始化的，但随着动态规划的进行，dp[i-1][j-v[i]] 会影响后续行的值。因此，后续行的 dp[i][j] 可能因为前一行的状态而变为有效状态（非 -1）。

对于上面的代码，我们还是可以进行优化操作的
1.利用滚动数组做空间上的优化
2.直接在原始的代码稍加修改即可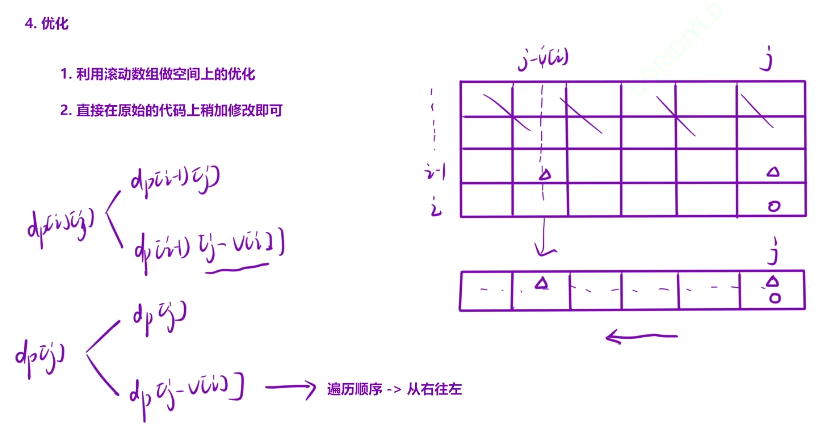image.png
删除所有的横坐标
修改一下j的遍历顺序

#include <iostream>#include<string.h>using namespace std;const int N=1010;int n,V,v[N],w[N];int dp[N];//默认初始化为0int main(){//读入数据cin>>n>>V;//循环输入数据到数组中去for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}//解决第一问for(int i=1;i<=n;i++){for(int j=V;j>=v[i];j--)//j表示的是容量，不能超过j{dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//这里最后记得加上w[i]的价值}}cout<<dp[V]<<endl;//解决第二问memset(dp,0,sizeof dp);//将dp表全部清空为0//-1的这种状态表示的是你想正好凑成价格为j是不存在的for(int j=1;j<=V;j++)dp[j]=-1;//在第一行位置，从1开始，都初始化为-1dp[0]=0;for(int i=1;i<=n;i++){for(int j=V;j>=v[i];j--)//j表示的是容量，不能超过j,{//在我们选择i位置之后，还有j还有剩余的，那么我们就去i-1位置去选j-v[i]价值的//我们这里一定要判断dp[j-v[i]]!=-1,就算说我们是能凑成j-v[i]这个体积的if(dp[j-v[i]]!=-1)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);//这里最后记得加上w[i]的价值}}cout<<(dp[V]==-1?0:dp[V])<<endl;//如果这里面的是值-1的话，那么我们就输入0就行了，如果不是-1的话，那么我我们就输出这个值就行了return 0;}

dp[j] 表示背包容量为 j 时，能够取得的最大价值。

你在遍历每个物品 i 时，从背包最大容量 V 开始倒序遍历（j = V; j >= v[i]; j--）。这确保了每个物品只被考虑一次，而不会在同一次循环中被多次选择。

我们只需要一个数组进行遍历就行了，并且是从右到左进行更新的操作
因为我们使用到dp[j]的时候需要dp[j]和dp[j-v[i]]，为了避免数据被覆盖了，找不到对应的数据，我们直接从右边到左边进行遍历的操作
image.png

不要强行解释优化后的状态表示以及状态转移方程

总之就是我们使用了滚动数组来实现了空间上的优化操作

50.分割等和子集

分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入： nums = [1,5,11,5]
输出： true
解释： 数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入： nums = [1,2,3,5]
输出： false
解释： 数组不能分割成两个元素和相等的子集。

从这个数组中挑选几个数，使这几个数之和满足sum/2

dp[i] [j]表示，从前i个数中选，所有的选法中，能否凑成j这个数，能凑成的话，里面存的就是true，不能的话就是falseimage.png
初始化：我们的i什么都不选，但是和达到j，所以第一行从第一个位置开始初始化为false
我们j是0，我们不选择一个元素就能凑到
所以第一列都初始化为1就行了
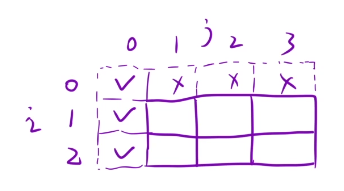
image.png

返回值就是dp[ n] [sum/2]
从前n个数中选，看看能不能凑成sum/2

class Solution{public:bool canPartition(vector<int>& nums){int sum=0;for(auto s:nums)sum+=s;if(sum%2==1)return false;//说明这个总和是奇数，那么我们就不能分为两份等量的数组了int n=nums.size();int aim=sum/2;//目标值vector<vector<bool>>dp(n+1,vector<bool>(aim+1));//其他位置默认初始化为false//初始化将第一列初始化为truefor(int i=0;i<=n;i++)dp[i][0]=true;//填表操作for(int i=1;i<=n;i++){for(int j=1;j<=aim;j++){dp[i][j]=dp[i-1][j];//这种情况就是不选择i位置的，直接去i-1位置选择aimif(j-nums[i-1]>=0)dp[i][j]=dp[i][j]||dp[i-1][j-nums[i-1]];//这种就是选择了i位置的，//dp[i][j]一开始存储的是不选择第 i 个元素时，使用前 i - 1 个元素能否组成和为 j 的结果，也就是 dp[i - 1][j] 的值,所以我们这里使用了或者，选择i位置或者是不选择i位置两种情况，只要一种返回true就行了}//因为我们创建了一行和一列，所以我们在使用nums找到原数组的话是找不到的，那么我们必须-1进行数组下标的映射操作}return dp[n][aim];//从0~n这个区间能不能找到和恰好为aim的序列}};

其实我们这是可以进行空间优化操作的
就是将横坐标删除，纵坐标
下面是空间优化后的版本

class Solution{public:bool canPartition(vector<int>& nums){int sum=0;for(auto s:nums)sum+=s;if(sum%2==1)return false;//说明这个总和是奇数，那么我们就不能分为两份等量的数组了int n=nums.size();int aim=sum/2;//目标值vector<bool>dp(aim+1);//其他位置默认初始化为false//初始化将第一列初始化为truedp[0]=true;//填表操作for(int i=1;i<=n;i++){for(int j=aim;j>=nums[i-1];j--){dp[j]=dp[j]||dp[j-nums[i-1]];//这种就是选择了i位置的，//dp[i][j]一开始存储的是不选择第 i 个元素时，使用前 i - 1 个元素能否组成和为 j 的结果，也就是 dp[i - 1][j] 的值,所以我们这里使用了或者，选择i位置或者是不选择i位置两种情况，只要一种返回true就行了}//因为我们创建了一行和一列，所以我们在使用nums找到原数组的话是找不到的，那么我们必须-1进行数组下标的映射操作}return dp[aim];//从0~n这个区间能不能找到和恰好为aim的序列}};

不用考虑这个空间优化后的状态表示的是什么

51.目标和

目标和

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

  • 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入： nums = [1,1,1,1,1], target = 3
输出： 5
解释： 一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入： nums = [1], target = 1
输出： 1

我们将正数和负数放在一起，然这些数分成两堆，左边正数的和加上右边负数的和就是我们最后的结果
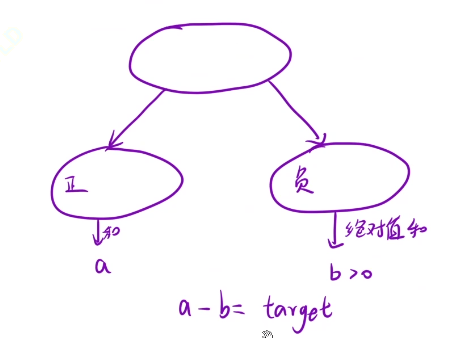
image.png
通过数学知识，我们是可以将负数这一块进行忽略掉的
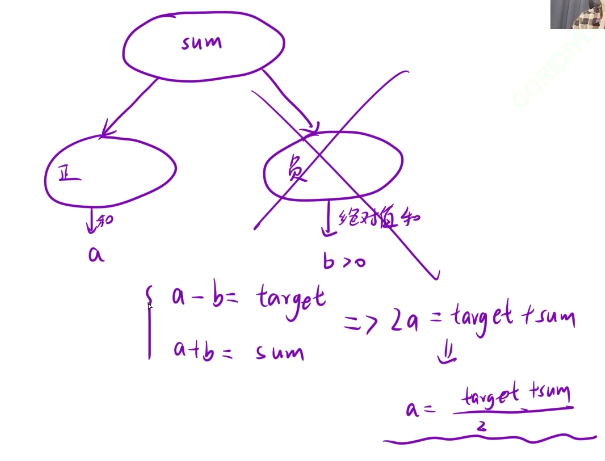
image.png
那么我们的问题就转化成了在数组中选择一些数，让这些数等于a，一共有多少种选法
image.png

正好可以装满这个背包，一共有多少种选法

dp[i] [j]表示：前i个数中选，总和正好等于j，一共有多少种选法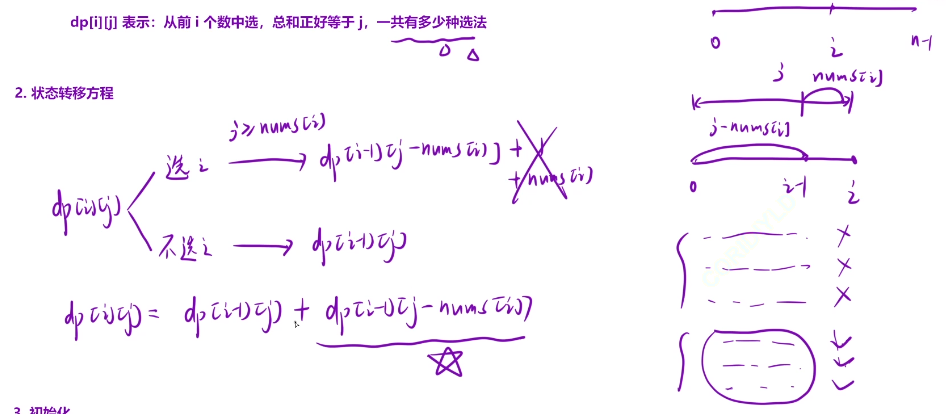image.png
就是将我们的两种情况加起来就行了
选i和不选i的两种情况

第一行是没有元素的，那么我们是不能凑出和为1和为2和为3的情况
我们只能凑出和为0的情况，那么第一行除了第一个格子初始化为1，其他的都初始化为0
第一列初始化还是有点麻烦的，因为我们需要考虑给到我们的数组中是否存在0
我们第一列其实是不需要进行初始化操作的，第一列的值更新是取决于第一排的值

class Solution{public:int findTargetSumWays(vector<int>& nums, int target){int n=nums.size();int sum=0;for(auto x:nums)sum+=x;int aim=(sum+target)/2;//处理下边界条件if(aim<0||(sum+target)%2==1)return 0;//如果sum是奇数的话，就是说除不尽的情况下，那么我们返回0vector<vector<int>>dp(n+1,vector<int>(aim+1));dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=aim;j++)//我们的第一列是没有进行初始化的，我们一定要从0开始{dp[i][j]=dp[i-1][j];//这种是i位置不选的情况，去i-1区域去找if(j-nums[i-1]>=0)dp[i][j]+=dp[i-1][j-nums[i-1]];//因为我们加了一行一列，所以我们这里是需要进行-1进行映射操作的，因为这里求的是可能操作的次数，所以我们进行一个累加的操作}}return dp[n][aim];}};

下面我将这个代码改成空间优化的版本
将横坐标都删除掉就行了

class Solution{public:int findTargetSumWays(vector<int>& nums, int target){int n=nums.size();int sum=0;for(auto x:nums)sum+=x;int aim=(sum+target)/2;//处理下边界条件if(aim<0||(sum+target)%2==1)return 0;//如果sum是奇数的话，就是说除不尽的情况下，那么我们返回0vector<int>dp(aim+1);dp[0]=1;for(int i=1;i<=n;i++){for(int j=aim;j>=nums[i-1];j--)//我们的第一列是没有进行初始化的，我们一定要从0开始{dp[j]=dp[j];//这种是i位置不选的情况，去i-1区域去找if(j-nums[i-1]>=0)dp[j]+=dp[j-nums[i-1]];//因为我们加了一行一列，所以我们这里是需要进行-1进行映射操作的，因为这里求的是可能操作的次数，所以我们进行一个累加的操作}}return dp[aim];}};

52.最后一块石头的重量 II

最后一块石头的重量 II
有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

  • 如果 x == y，那么两块石头都会被完全粉碎；
  • 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入： stones = [2,7,4,1,8,1]
输出： 1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入： stones = [31,26,33,21,40]
输出： 5

在数组中选择一些数，这些数的和尽可能接近sum/2

这个就是每次随机选两个数，然后在其中一个数的前面加上一个负号，然后两个数进行相加的操作就可以得出了差值

这个和上面的目标和是差不多的，都是有正数和负数进行相加操作

我们让所有的正数的和为a，所有的负数和为b

我们要的是a-b的绝对值尽可能最小
这里的a+b的和是sum
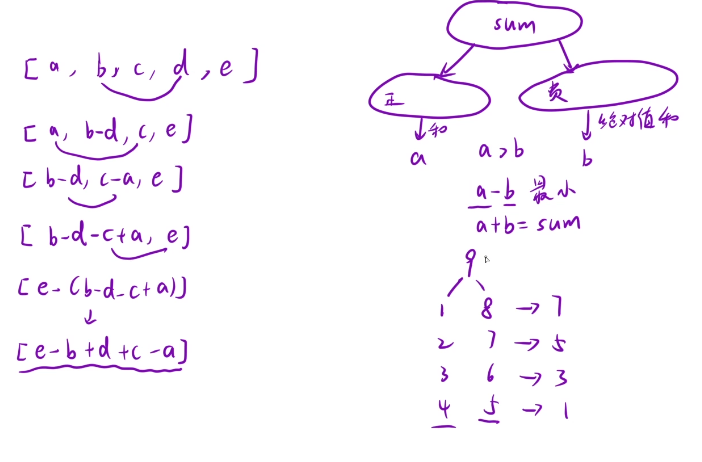
image.png

就是如果想要差值最小的话，那么我们的a和b就得接近sum的一半image.png
越接近sum的一半，那么两者的差就是最小的

那么问题转化为：在数组中选择一些数，让这些数的和尽可能接近总和的一半
dp[i] [j]表示：从前i个数中选，总和不超过j，此时的最大和image.png
dp[n] [sum/2]仅仅是我们a的值，因为a+b=sum
所以我们的b=sum-a
但是最后我们最小的值就是sum-b-a，这个就是最小值了
所以返回值是sum-dp[n] [sum/2]-dp[n] [sum/2]

class Solution 
{
public:int lastStoneWeightII(vector<int>& stones) {int sum=0 ;for(auto x:stones)sum+=x;int m=sum/2;int n=stones.size();vector<vector<int>>dp(n+1,vector<int>(sum/2+1));for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){dp[i][j]=dp[i-1][j];//这个即是不选择i的情况，直接去i-1区间进行查看if(j-stones[i-1]>=0)dp[i][j]=max(dp[i][j],dp[i-1][j-stones[i-1]]+stones[i-1]);} }return sum-2*dp[n][m];}
};

下面是空间优化的版本，将横坐标删除就行了

class Solution{public:int lastStoneWeightII(vector<int>& stones){int sum=0 ;for(auto x:stones)sum+=x;int m=sum/2;int n=stones.size();vector<int>dp(sum/2+1);for(int i=1;i<=n;i++){for(int j=m;j>=stones[i-1];j--){dp[j]=max(dp[j],dp[j-stones[i-1]]+stones[i-1]);}}return sum-2*dp[m];}};

为什么返回值是这个呢？

因为我们在这个题的时候，代码思路计算的是最接近sum/2的值，
就是在前i个区间内，找到几个数的和接近sum/2
这个其实就是a了，就是dp[ n] [m]了，在n区间内找到接近于m的，m就是sum/2
a+b=sum，b=sum-a

最小值=sum-b-a

我们得到的dp[n ] [m]仅仅是我们的a了

image.png
image.png

http://www.dtcms.com/a/312583.html

相关文章：

  • kafka与其他消息队列（如 RabbitMQ, ActiveMQ）相比，有什么优缺点？
  • 渗透作业4
  • 华为云云服务高级顾问叶正晖：华为对多模态大模型的思考与实践
  • 在AI时代，如何制定有效的职业规划？AI时代职业规划与产品经理角色
  • ThinkPHP8.x控制器和模型的使用方法
  • MySQL学习之MVCC多版本并发控制
  • React中的Hooks
  • 量子态演化算符性质与形成原因总结
  • 决策树分类实战：从数据到模型优化
  • 代驾管理系统：智慧出行的重要支撑
  • 8.3 滑窗 |栈|阶乘判断
  • vector＜int＞ adjList[MAX] 和 vector＜int＞ adjList(MAX)的区别【C++】
  • 记录NVIDIA Orin启动流程，镜像文件，AB双分区，ota升级
  • STM32复位电路解析
  • Java常用英语单词
  • adb 与pad 交互方法
  • PPT自动化 python-pptx - 9: 图表（chart）
  • 服务器中切换盘的操作指南
  • Jetson Orin NX/NANO+ubuntu22.04+humble+MAVROS2安装教程
  • Kafka——常见工具脚本大汇总
  • /usr/bin/ld: 找不到 -lev
  • stm32f103重新上电后前面的打印内容无法打印出来的原因
  • Springboot 04 starter
  • 分布式文件系统05-生产级中间件的Java网络通信技术深度优化
  • ClickHouse Windows迁移方案与测试
  • HiveMQ 2024.9 设计与开发文档
  • 知识随记-----MySQL 连接池健康检测与 RAII 资源管理技术
  • Timer串口常用库函数（STC8系列）
  • Docker--解决x509: certificate signed by unknown authority
  • 系统学习算法：专题十六 字符串