从传热学基础到有限元弱形式推导：拆解热传导问题Matlab有限元离散核心

导读：上一篇文章热传导问题Matlab有限元编程-从零搭建热传导求解器-含案例源码 正式向读者和粉丝推荐了我的热传导问题领域有限元编程教程，收到了学习者强烈反响。不少《Matlab有限元编程从入门到精通》订阅用户再次把它添加到自己学习计划，甚是欣慰！

本文配合我的仿真秀官网视频课程《热传导问题Matlab有限元编程》第2~4讲，主要带大家了解传热学的基本概念、控制方程及弱形式推导，就像我们学习结构力学有限元求解同样要了解结构力学和弹性力学中偏微分控制方程的建立。熟悉有限元基本理论的小伙伴应该清楚，在带入形函数进行有限元离散之前都需要将控制方程进行弱化，将原有强形式改写弱形式。所以我们还会介绍热传导方程的弱形式推导以及带入形函数进行有限元离散的过程，这个过程会涉及伽辽金加权残值方法、格林公式（分部积分）、泛函驻值等弱形式推导过程中用到的理论知识。文章最后阐述了我对一个问题的理解：为什么有限元离散需要基于控制方程的弱形式？

热传导问题Matlab有限元编程 【含案例源码】：​www.fangzhenxiu.com/course/12989155/

Matlab有限元编程从入门到精通40讲【含案例源码】：​www.fangzhenxiu.com/course/5190666/

一、传热学基本概念

教科书里的概念我就不在这里赘述，为了让大家对传热学有一个更感性的认识，这里我通过类比结构力学领域的相关概念去帮助大家理解传热学的基本概念。传热学所要求解的就是基于傅里叶热传导定律建立的传热学控制方程，最终计算得到稳态或瞬态温度场。在结构力学问题中求解场变量是位移, 是向量场, 而热传导问题中场变量是温度, 是标量场。因此, 热传导问题要比力学问题相对简单些，控制方程的建立也会更简单一些。许多热传导物理量可以与弹性力学问题中的物理量进行类比, 比如位移与温度, 比热容与密度 (对于瞬态问题表示场变量的惯性效应, 稳态问题不起作用)。节点热流量和节点力，对流换热表面热通量与表面分布力，位移边界条件与固定温度边界条件，热源与体积力。注意区分热通量与热流量的概念，热通量（heat flux）表示单位时间单位面积内通过的能量，单位 W/m^2，热通量也叫热流密度；热流量（heat flow）可以简单理解为热量，表示一段时间内热量的变化,重点是量, 不存在单位面积体积的概念, 单位是 W , 可以简单理解为热通量在边界上的面积积分就是热流量，热流量也称热流率。

由于求解域几何形状以及变温条件的复杂性,依靠传统的解析方法要精确地确定温度场往往是不可能的,有限元法却是解决上述问题的方便而有效的工具。在进入热传导问题有限元法的具体讨论以前,首先将热传导问题的基本方程（控制方程）作简单的介绍。

二、热传导控制方程

对于一个三维实体，t时刻的瞬态温度T(x,y,z,t)的计算公式如下：

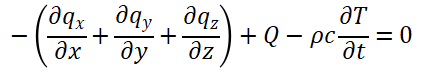
（1）

其中 qx,qy,qz为热通量分量, 将

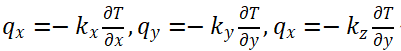
代入式(1)可得：

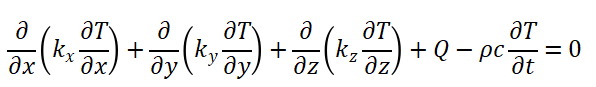
（2）

其中: x,y,z 为热传导主方向; kx,ky,kz分别为 x,y,z方向的热传导系数; Q 是单位体积发热率; ρ 是材料密度; C是比热。对于稳态传热问题，公式 1 中的时间偏导项可忽略不计。初始条件如下；

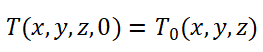
（3）

边界条件分为以下四种：

1) 温度边界条件:

（4）

2) 热通量边界条件:

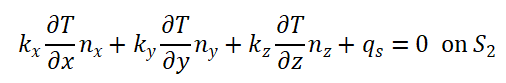
(5)

3) 对流换热边界条件:

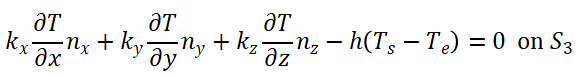
(6)

4) 热辐射边界条件:

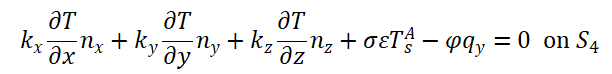
(7)

其中：T*为特定嗢度；q为热通量；h为对流换热系数；nx,ny,nz分别为边界法线方向；Ts为表面温度；Te为环境温度； σ 为 Stefan-Boltzman 常数； δ 为表面辐射系数； ψ 为表面吸收系数；qr为入射热通量；

S1,S2,S3为边界表面；微分方程(2)是热量平衡方程，也叫控制方程。微分方程表明:微体升温所需的热量应与传入微体的热量以及微体内热源产生的热量相平衡。 S1边界上给定温度,称为第一类边界条件,它是强制边界条件。S2边界上给定热流量qs ,称为第二类边界条件,当q=0时就是绝热边界条件。S3 边界上给定对流换热的条件,称为第三类边界条件第二、三类边界条件是自然边界条件。

当在一个方向上,例如z方向温度变化为零时,方程 (2) 就退化为二维问题的热传导微分方程:

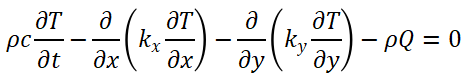
（8）

对于轴对称问题,在柱坐标中场函数 ϕ(r,z,t) 应满足的微分方程,且

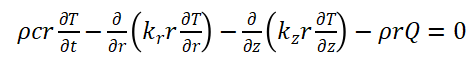
(9)

求解瞬态温度场问题是求解在初始条件下,即在

条件下满足瞬态热传导方程及边界条件的场函数T,T应是坐标和时间的函数。如果边界上的,T,qTa及内部的Q不随时间变化,则经过一定时间的热交换后,物体内各点温度也将不再随时间而变化,即

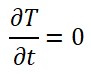
(10)

这时瞬态热传导方程就退化为稳态热传导方程了。求解稳态温度场的问题就是求满足稳态热传导控制方程及边界条件的场变量T，T 只是坐标点的函数,与时间无关。

稳态热传导问题即稳态温度场问题与时间无关。由方程的等效积分形式的伽辽金方法,可以建立与方程相等效的变分原理。和弹性静力学相同，采用插值函数的有限元进行离散以后,从泛函取驻值可以直接得到有限元求解方程。在结构力学问题有限元求解中所采用的单元和相应的插值函数在此都可以使用。主要的不同是场变量,在结构力学问题中,场变量是位移,是向量场；在热传导,问题中，场变量是温度，是标量场。

瞬态热传导问题，即瞬态温度场问题, 是依赖于时间的。微分方程等效积分形式离散后,得到的是一阶常微分方程组,不能直接求解。求解方法与动力学问题类似，可以采用直接积分法或模态叠加法，本课程重点围绕直接积分法讲解。主要涉及直接积分法的算法步骤和解的稳定性问题。

三、稳态热传导问题的弱形式

上一节了解了传热学中的基本概念以及热传导控制方程的形式，那接下来我们就需要对控制方程进行有限元离散。熟悉有限元的小伙伴应该清楚，在带入形函数进行有限元离散之前都需要将控制方程进行弱化，将原有强形式改写弱形式。所以我们这节首先要进行热传导方程的弱形式推导，然后再讲有限元离散的过程。

可能听到这里，大多数人会感到头大，因为这部分内容主要是关于有限元方法的数学原理的，涉及的数学理论较多。但为啥还要讲这部分内容呢，不讲行不行，我不懂这部分内容还能做有限元编程吗？答案是不讲完全可以，不懂这部分内容也可以做有限元编程。因为我们当前用到的大多数单元的有限元离散的推导过程在教科书、网络上、文献中都可以找到，最终我们编程并不需要中间的推导，而只要知道最后单元的结构刚度矩阵、热导率矩阵等的具体表达式即可，当然还有其他物理领域的矩阵，叫什么不重要，可以理解为广义的刚度矩阵。有了这个矩阵的表达式，我就能用各种编程语言、在各种架构下去开发这样的单元。

那我们为啥还要讲弱形式和有限元离散推导过程呢？因为对于一些在当前文献中很难找到的特殊单元的刚度矩阵改怎么办呢？那就需要你亲自去推导对应的表达式，只有具备从弱形式推导刚度矩阵的能力，才能完成从0到1的突破，对于复杂物理问题才能建立其有限元数值求解真正的桥梁，解决的是从无到有的问题。但能做到这一点要有很强的理论功底，我在这里只是抛砖引玉吧，希望能对大家有所启发。

有很多方法可以将问题的物理形式转换成有限元离散后的形式。如果物理问题是由偏微分方程描述的，则经常使用的是伽辽金方法(Galerkin method)。如果物理问题是由泛函最小化描述的，则经常使用变分公式(variational formulation)将其转换为有限元方程。

利用加权余量的伽辽金方法可以导出与三维稳态热传导问题的微分方程相等效的加权残值方程；同样遵循虚功原理、最小势能原理或者“广义能量原理”将物理问题转换为泛函最小化，利用变分原理也可以建立与其相等效的弱形式。两种方法殊途同归。接下来我们针对热传导控制方程运用两种方法推导其弱形式。

1、加权残值法弱形式

第一种方法，伽辽金加权残值法，具体来讲就是选择权函数（满足本质边界条件），构造加权残值积分。将方程乘以权函数并在整个域 Ω 内积分，对包含二阶导数的扩散项进行分部积分（二阶偏导项），应用格林公式（Green's identity）。格林公式将体积积分中的二阶导数项 转化为一阶导数项，并自然而然的引入边界积分项。这一步骤的核心目的是降低导数的阶数，使得弱形式仅需 一阶可到，从而允许使用分片多项式形函数（如线性元）进行离散。这里直接给出推导得到的加权残值方程对应的弱形式。

考虑二维稳态传热问题的强形式方程：

边界条件： - Dirichlet边界：

- Robin边界：

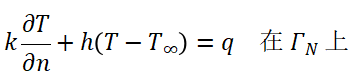
（1）构造加权残值积分

选择权函数v(x,y)∈H1(Ω)，且满足 v=0 在 ΓD 上（满足本质边界条件）。将方程乘以 v 并在整个域 Ω 内积分：

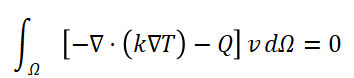
（2）应用分部积分法

对二阶导数项进行格林公式展开：

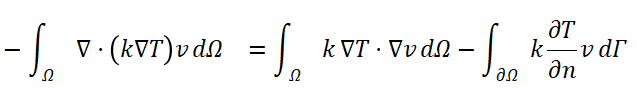
• 格林公式将体积积分中的二阶导数项 ∇⋅(k∇T) 转化为一阶导数项 k∇T⋅∇v 的积分，并引入边界积分项 ∫∂Ωk∂T∂nv dΓ。

• 这一步骤的核心目的是降低导数的阶数，使得弱形式仅需 T∈H1(Ω)（一阶可积函数空间），而非 H2(Ω)，从而允许使用分片多项式形函数（如线性元）。

（3）处理边界积分项

将边界分解为Dirichlet和Neumann部分：

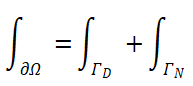
-在ΓD上：( v=0 ) 导致积分消失-在ΓN上：代入自然边界条件

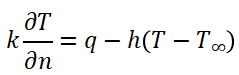
（4）最终弱形式方程

整理得到弱形式表达式：

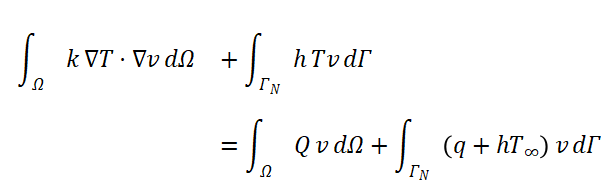
2、变分原理弱形式

同样利用广义能量原理（类比力学中的最小势能原理），力学中的势能泛函： 弹性体的总势能 Π=应变能−外力做功Π=应变能−外力做功，最小化 Π对应平衡方程。传热中的“广义能量”泛函：J(T) 包含导热项（类比“应变能”）、内热源项（类比“外力做功”）和边界对流项，形式上模仿能量泛函的构造。

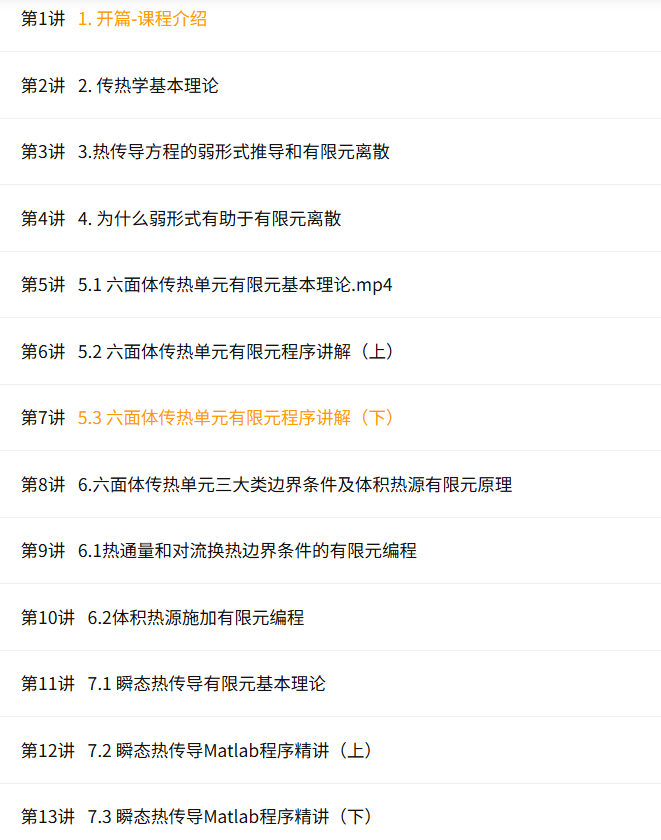
可以得到泛函表达式，这里不进行推导, 直接给出变分原理中的泛函的表达式如下:

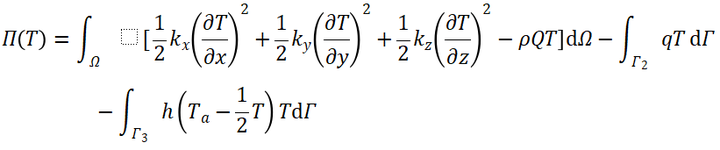
（11）

• 弱形式中仅含一阶导数项，适合有限元离散。

• 自然边界条件（上的热流或对流）自动融入方程右侧的边界积分项。

• Dirichlet 边界条件通过约束 v=0 在边界上隐式满足，推导过程中消掉。

可以验证,从上述泛函的驻值条件

得到泛函的欧拉方程就是三维稳态热传导问题的微分方程和边界条件。亦即表示泛函的变分是和该微分方程及边界条件相等效的。弱形式可视为某个泛函的极值条件。因此利用

可以建立可进行有限元离散的弱形式：

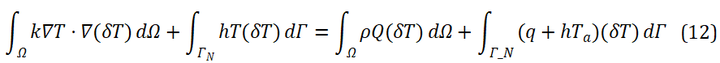
这里的δT相当于加权残值法中的权函数v

3、基于弱形式的有限元离散

将求解域 Ω 离散为有限个单元体,在典型单元内各点的温度T可以近似地由单元结点温度Ti插值得到

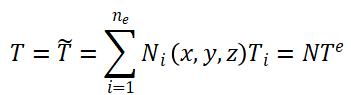
（13）

其中ne是每个单元的结点数; Ni 是C0型插值函数,它亦具有下述性质:

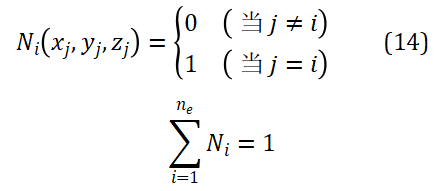
将温度场离散表达式（13）带入公式（11）表示泛函方程，利用泛函的驻值条件

即可得到稳态热传导问题的有限元求解方程

方程中的K矩阵对于传热问题可称为热传导矩阵

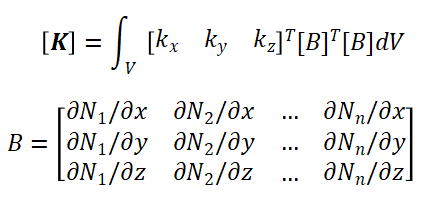
四、弱形式在有限元离散中的必要性分析

为什么有限元离散需要基于控制方程的弱形式呢？

强形式需求：原始微分方程包含二阶导数项（如

若直接离散，解函数，要求解函数

（一阶导数连续）。然而，有限元中常用的分片多项式形函数（如线性元）仅满足 ( C^0 ) 连续性（函数连续，但导数不连续）。

弱形式松弛：通过分部积分将二阶导数降阶后，仅需

（一阶弱可导），允许使用C0连续的分片多项式基函数（如线性元）

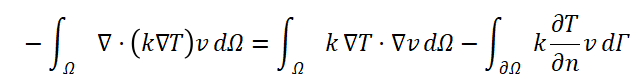
弱形式的Neumann/Robin边界可自动融合：自然边界条件通过边界积分项直接引入方程；而强形式中的边界条件：Neumann/Robin 条件（如热流或对流边界）需显式施加，可能涉及复杂的导数计算。

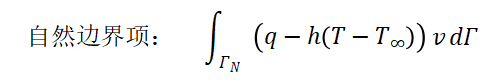
Dirichlet边界隐式施加：通过约束权函数 实现

从数值计算的复杂性来看，由于基函数C0连续要求，弱形式具有较好的网格适应性，对于边界条件的处理也更简单，代码实现相对容易。当然有限元中也有C1单元的运用，如梁板壳单元。

真正考验一个人有限元功底就是基于弱形式推导刚度矩阵的能力。当现有文献直接给出了刚度矩阵推导的过程，那程序实现起来相当于换一种符号去表达相同的公式，但只有具备从弱形式推导刚度矩阵的能力，才是完成从0到1的突破，对于复杂物理问题实现了数值求解。

更多内容可参考我的《热传导问题Matlab有限元编程》视频课程！

五、为什么要学习这门课程

回到我们的课程，热传导分析是工业设计的重要支柱，从电子芯片的散热优化到航天器的热防护设计，从金属成型的热处理到建筑节能的温度场模拟，这些看似迥异的工程问题背后都遵循着相同的传热学规律。

本课程将带您突破有限元在结构力学领域的应用范围，在Matlab平台上构建全新的传热问题的有限元求解体系，并通过解决热固耦合问题，将有限元在传热领域和结构力学领域的应用融会贯通，最后你会惊喜地发现：无论是热传导方程还是结构力学方程，其有限元求解的本质，竟都扎根于偏微分方程的数值离散之道。以下是我认为学习这门课程价值所在：

1、全链路实战：从理论到工业级代码落地。课程内容覆盖传热学基础、有限元弱形式推导、稳态 / 瞬态求解、热固耦合等核心理论，配套 2D/3D 单元（tri3/quad4/tet4/hex8）代码实现，对标 ANSYS 精度（误差 <1%），真正做到 “理论懂原理，编程能上手”。

2、破解商业软件 “黑箱”：掌握结果背后的逻辑。深入讲解三类边界条件（固定温度、热流密度、热对流）、体积热源施加的底层算法，让你理解仿真结果的误差来源、合理性判断依据，不再盲目依赖软件输出。针对非常规问题（如特殊热源、复杂耦合场景），教你开发专用工具，满足科研中的参数化研究、优化设计等定制需求，为论文或项目提供独家数值支持。

3、热固耦合全掌握：从温度场到应力场一站式求解。涵盖间接耦合（先求温度场再算热应力）和直接耦合（同步求解温度、位移、应变场），完整复现工业级热 - 结构耦合仿真流程，适应机械、航空航天等多领域需求。