微积分思想的严密性转变 | 极限、逼近与程序化
注:本文为 “微积分历程” 整理。
zhihu 引文,略作重排。
如有内容异常,请看原文。
微积分究竟是什么?
原创 长尾君 长尾科技 发布于 2019-12-01 17:46・湖北
微积分概念抽象,理解难度较大。本文将详细阐述如何思考定积分问题。

微积分的重要性不言而喻。对于数学研究者而言,未掌握微积分,几乎无法开展任何工作。牛顿因发明微积分,与阿基米德、高斯并称为世界三大数学家。然而,微积分并非难以理解,其基本思想极为简单,这也是众多初中生能够学习微积分的原因。
01 从面积说起
自小学起,我们便学习各种求面积的公式,如长方形、三角形、圆、梯形等。而“求阴影部分的面积”常成为学习难点。
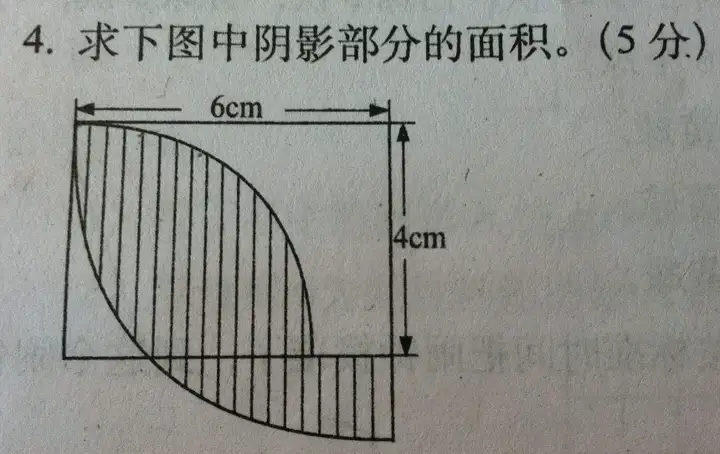
问题在于,世界上存在无数种图形,不可能记住无数种面积公式。更棘手的是,许多图形并无现成的面积公式。例如,随手画出一条曲线,其围成的面积该如何计算?尽管无法直接找到公式,但理论上应能计算出其面积。这一问题促使数学家们思考。
阿基米德最早探索了抛物线问题:如何求抛物线与直线围成的面积?抛物线是物体被抛向空中时的轨迹。如图,抛物线与直线 BC 围成一个弓形。

阿基米德的方法是:利用无数个三角形逼近弓形的面积。他首先画了一个大三角形 △ABC\triangle ABC△ABC,其面积小于弓形面积,少了左右两边两个小弓形的面积。继续用三角形逼近这两个小弓形,依次类推,可无限重复。
阿基米德发现,每次新画的三角形面积是上一轮三角形面积的 14\frac{1}{4}41。设大弓形的面积为 SSS,则有:
S=△ABC+14△ABC+(14)2△ABC+(14)3△ABC+…S = \triangle ABC + \frac{1}{4} \triangle ABC + \left( \frac{1}{4} \right)^2 \triangle ABC + \left( \frac{1}{4} \right)^3 \triangle ABC + \ldots S=△ABC+41△ABC+(41)2△ABC+(41)3△ABC+…
阿基米德通过计算前几项,猜测 SSS 应等于 43△ABC\frac{4}{3} \triangle ABC34△ABC。他通过证明,如果 SSS 大于或小于 43△ABC\frac{4}{3} \triangle ABC34△ABC,都会出现矛盾,因此 SSS 只能等于 43△ABC\frac{4}{3} \triangle ABC34△ABC。
阿基米德成功求出抛物线与直线围成的弓形面积,结果为 43△ABC\frac{4}{3} \triangle ABC34△ABC。他所用的这种方法被称为“穷竭法”。
02 一千年以后
时光荏苒,转眼间已是一千八百年后的十七世纪。
穷竭法虽然可以精确地计算出一些曲线围成的面积,但其存在一个显著的缺陷:对于不同曲线围成的面积,需要使用不同的图形去逼近。例如,在上述例子中使用的是三角形,而在其他情况下可能需要使用其他图形。不同的图形需要不同的证明技巧,这无疑增加了计算的复杂性。
到了十七世纪,数学家们开始统一使用矩形(长方形)进行逼近:无论何种曲线围成的图形,都用无数个矩形去逼近,且沿着 xxx 轴进行切割。这一方法在操作上更为简便。
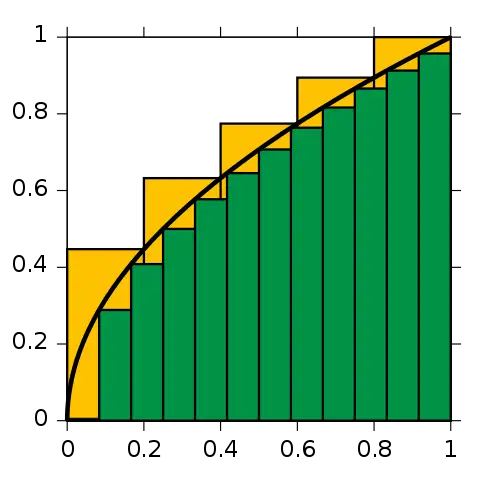
以抛物线为例,我们考虑最简单的抛物线 y=x2y = x^2y=x2。其图像大致如下(对于每一个 xxx 的值,yyy 的值为其平方)。接下来,我们具体计算这条抛物线在 0 到 1 之间与 xxx 轴围成的面积。
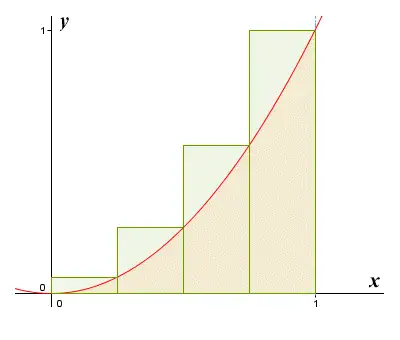
我们利用矩形去逼近原图形。可以想象,矩形的数量越多,这些矩形的面积之和就越接近曲线围成的面积。这一思路与穷竭法相似,但更容易理解。
假设 0 到 1 之间被平均分成了 nnn 份,那么每一份的宽度为 1n\frac{1}{n}n1。矩形的高度即为函数的纵坐标值,可以通过 y=x2y = x^2y=x2 计算得出。因此,第一个矩形的高度为 (1n)2\left( \frac{1}{n} \right)^2(n1)2,第二个矩形的高度为 (2n)2\left( \frac{2}{n} \right)^2(n2)2,第三个矩形的高度为 (3n)2\left( \frac{3}{n} \right)^2(n3)2……
已知矩形的宽度和高度,将其相乘即可得到矩形的面积。因此,所有矩形的面积之和 SSS 可以表示为:
S=(1n)2⋅1n+(2n)2⋅1n+(3n)2⋅1n+…+(nn)2⋅1nS = \left( \frac{1}{n} \right)^2 \cdot \frac{1}{n} + \left( \frac{2}{n} \right)^2 \cdot \frac{1}{n} + \left( \frac{3}{n} \right)^2 \cdot \frac{1}{n} + \ldots + \left( \frac{n}{n} \right)^2 \cdot \frac{1}{n} S=(n1)2⋅n1+(n2)2⋅n1+(n3)2⋅n1+…+(nn)2⋅n1
这是一段普通的化简过程。只要知道平方和公式如下,即可迅速理解:
12+22+32+…+n2=n(n+1)(2n+1)61^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n + 1)(2n + 1)}{6} 12+22+32+…+n2=6n(n+1)(2n+1)
因此,我们得到 nnn 个矩形面积之和的表达式:
S=1n3⋅n(n+1)(2n+1)6=(n+1)(2n+1)6n2=2n2+3n+16n2=13+12n+16n2\begin{aligned} S & =\frac{1}{{{n}^{3}}}\cdot \frac{n(n+1)(2n+1)}{6} \\ & =\frac{(n+1)(2n+1)}{6{{n}^{2}}} \\ & =\frac{2{{n}^{2}}+3n+1}{6{{n}^{2}}} \\ & =\frac{1}{3}+\frac{1}{2n}+\frac{1}{6{{n}^{2}}} \end{aligned}S=n31⋅6n(n+1)(2n+1)=6n2(n+1)(2n+1)=6n22n2+3n+1=31+2n1+6n21
由于 nnn 是矩形的个数,nnn 越大,矩形的数量就越多,那么这些矩形的面积之和就越接近曲线围成的面积。因此,当 nnn 趋向于无穷大时,从“直觉”上认为,这些矩形的面积之和就应该等于抛物线围成的面积。
与此同时,当 nnn 趋向于无穷大时,表达式中的后两项 12n\frac{1}{2n}2n1 和 16n2\frac{1}{6n^2}6n21 从“直觉”上来看应该无限趋近于 0,或者说等于无穷小,似乎可以忽略不计。
因此,当 nnn 趋向于无穷大时,面积 SSS 只剩下第一项 13\frac{1}{3}31。于是,我们得到了抛物线 y=x2y = x^2y=x2 与 xxx 轴在 0 到 1 之间围成的面积 SSS,结果恰好为 13\frac{1}{3}31。
在阅读这一计算方法后,读者可能会有自己的想法。或许会觉得这种方法更简单、更神奇,或者有其他不同的感受。然而,需要注意的是,在这一段中,我们使用了一些诸如“直觉上”“应该”“似乎”等不够精确的表述。在大家的印象中,数学应当是一门最精确、最严密的学科,为何此处会使用这些模糊不清的词汇呢?
03 严密性与实用性
然而,这正是问题所在:并非我们不想讲清楚,而是当时根本无法讲清楚。不仅我们无法讲清楚,就连牛顿和莱布尼茨也无法做到。这与阿基米德使用穷竭法求面积时的精确性形成了鲜明对比。
使用穷竭法求面积时,例如为了得到 43△ABC\frac{4}{3} \triangle ABC34△ABC,阿基米德通过证明,如果面积大于 43△ABC\frac{4}{3} \triangle ABC34△ABC,会出现矛盾;如果面积小于 43△ABC\frac{4}{3} \triangle ABC34△ABC,同样会出现矛盾。因此,面积必须等于 43△ABC\frac{4}{3} \triangle ABC34△ABC。这种方法虽然操作上较为繁琐,但在逻辑上无懈可击。

然而,在十七世纪,我们是如何得到抛物线与 xxx 轴围成的面积等于 13\frac{1}{3}31 的呢?我们得到了 nnn 个矩形的面积公式:
S=13+12n+16n2S = \frac{1}{3} + \frac{1}{2n} + \frac{1}{6n^2} S=31+2n1+6n21
接着,我们觉得当 nnn 越来越大时,后两项 12n\frac{1}{2n}2n1 和 16n2\frac{1}{6n^2}6n21 的值会越来越小。当 nnn 变成无穷大时,这两项应该就是无穷小。于是,我们直接将其舍去,因此面积 SSS 只剩下第一项 13\frac{1}{3}31。
然而,问题在于:无穷小究竟是多小?从直觉上来看,无论 nnn 取多大,12n\frac{1}{2n}2n1 和 16n2\frac{1}{6n^2}6n21 都应该是大于 0 的。我们可以直接舍去 0,但对于并不等于 0 的数,我们能否直接舍弃呢?这种做法的合法性依据在哪里?
相较于古希腊的穷竭法,十七世纪的这种计算方法虽然更为简单,但由于缺乏严密性,因此当时的数学家们并不愿意使用。他们宁可选择使用更为繁琐但在逻辑上无懈可击的穷竭法,因为在他们看来:逻辑的严密性远比计算结果的实用性重要。
在严密性与实用性的取舍上,东西方走上了截然不同的两条道路。古代中国毫不犹豫地选择了实用性。他们需要数学来帮助国家计算税收、计算桥梁房屋等建筑工程以及解决商业活动中的各种经济问题。因此,《九章算术》中全是关于如何巧妙计算的各种方法。这也使得古代中国出现了众多能工巧匠,设计出了许多精巧的建筑工程。

西方则截然相反。古希腊人坚定不移地选择了严密性。他们需要严密的逻辑来帮助他们认识世界的本原,了解世界是由什么组成的,以及为何世界会是现在这个样子。因此,《几何原本》中通过从 5 个显而易见的公理出发,运用严密的逻辑逐步推导出 400 多个定理,即便这些定理本身并不显而易见。因此,西方能够诞生现代科学。
失去简单性,数学会失去很多;然而,失去严密性,数学将失去一切。至于如何使其变得严密,我们将在后续内容中详细阐述。
04 初见积分
从开篇到现在,我们一直在讨论面积问题,而微积分的名字中恰好有一个“积”字。那么,这两个“积”字之间是否存在联系呢?答案是肯定的。
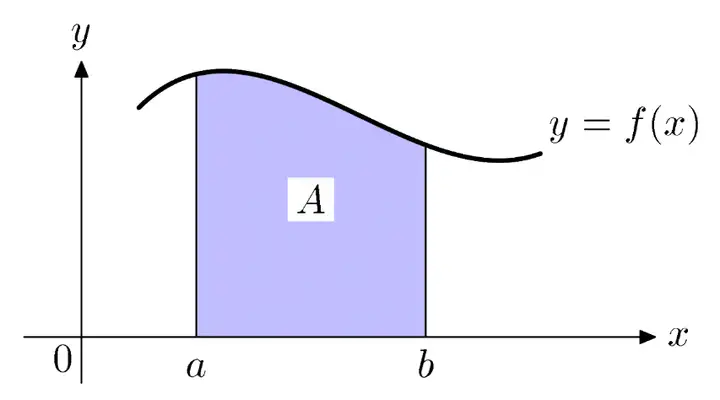
我们可以将微积分拆分为“微分”和“积分”两个部分。积分这一概念最初被创造出来,是用来表示“由无数个无穷小的面积组成的面积 SSS”。

如上图所示,如果一条曲线 y=f(x)y = f(x)y=f(x) 与 xxx 轴在 aaa 和 bbb 之间围成的面积为 SSS,那么,我们可以用积分来表示这部分面积:
S=∫abf(x)dxS = \int_{a}^{b} f(x) \, dx S=∫abf(x)dx
在第二节的例子中,我们求的是抛物线 y=x2y = x^2y=x2 与 xxx 轴在 0 到 1 之间围成的面积。因此,此处 f(x)=x2f(x) = x^2f(x)=x2,a=0a = 0a=0,b=1b = 1b=1,且最终结果为 13\frac{1}{3}31。将这些值代入上述公式,可以得到:
∫01x2dx=13\int_{0}^{1} x^2 \, dx = \frac{1}{3} ∫01x2dx=31
也就是说,该积分值等于 13\frac{1}{3}31,代表了这块面积。
为了加深对积分表达式的理解,我们再回顾一下求抛物线围成面积的过程:我们用无数个矩形将 0 到 1 之间分成无穷多份,然后将所有矩形的面积相加。由于矩形的面积为底乘以高,而这个高恰好是函数的纵坐标 yyy。
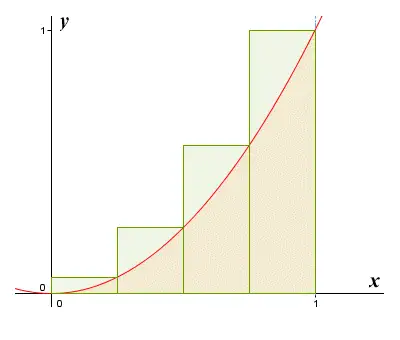
因此,当我们用无数个矩形去逼近原面积时,每个矩形的底自然就变成了无穷小,这个无穷小的底就是上述公式中的 dxdxdx。而 x2x^2x2 表示的是函数的纵坐标,即矩形的高。底 dxdxdx 与高 x2x^2x2 相乘,不就是在求面积吗?再观察这个表达式,与前面求面积的过程是否一致?
∫01x2dx=13\int_{0}^{1} x^2 \, dx = \frac{1}{3} ∫01x2dx=31
然而,仍需强调的是,此处将 dxdxdx 视作一个无穷小的底,将积分视作求面积,这只是微积分创立初期的看法。这种看法虽然符合我们的直觉,但在逻辑上并不严密。这种无穷小量 dxdxdx 也曾招致许多人的批评(例如贝克莱大主教),并引发了第二次数学危机。这场危机直到 19 世纪柯西等人完成了微积分的严密化之后才得以彻底解决。随着微积分的涅槃重生,我们对这些基本概念的看法也将发生根本性的改变。
关于求面积的问题到此为止。“用一些图形去无限逼近曲线图形”的思想由来已久,穷竭法在古希腊时期就已经相当成熟。中国魏晋时期的数学家刘徽使用割圆术去逼近圆周率,也是基于这种思想。到了 17 世纪初,这些思想并没有太大的改变。由于这些解法较为复杂且难以扩展,因此当时大家对它们的关注度并不高。
然而,没有人会想到:破解这种求曲线面积(求积分)的关键,竟然藏在一个看起来与它毫无关联的东西身上,这个东西就是微积分名字里的另一半:微分。当牛顿和莱布尼茨意识到积分与微分之间的内在关系之后,数学迎来了一次空前的大发展。
05 直线与斜率
关于求面积(积分)的问题暂且告一段落,接下来我们来看看微积分里的另一半:微分。
微分学的基本概念是导数。关于导数,我们在麦克斯韦方程组的积分篇中曾经介绍过一次,在微分篇中又介绍过一次(在那里还介绍了升级版的偏导数)。此处,作为主角,我们再次对其进行详细阐述。
当我们爬山时,山越陡峭,攀登难度越大;骑车时,路面坡度越大,骑行难度越高。一个平面的坡度越大,倾斜得越厉害,我们越难前进。那么,我们该如何衡量这种倾斜程度呢?

在平面上画一条直线,我们可以直观地看出这条直线的倾斜程度,并且不难发现:无论在直线的何处,其倾斜程度都是一样的。
因此,我们可以用一个量来描述整条直线的倾斜程度,这个概念被形象地命名为“斜率”。
那么,一条直线的斜率该如何计算呢?这一想法也很直观:建立一个坐标系,观察当直线在 xxx 轴上改变 Δx\Delta xΔx 时,其在 yyy 轴上的改变量 Δy\Delta yΔy 是多少。如果 Δx\Delta xΔx 是固定的,那么显然 Δy\Delta yΔy 越大,这条直线就越倾斜,斜率也就越大。
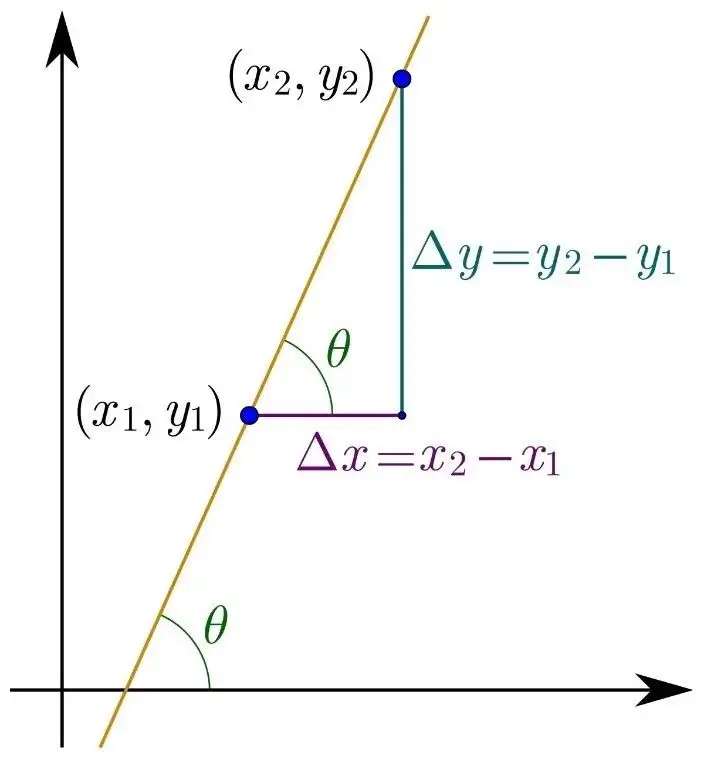
这与我们判断跑步速度的原理相似:给定一个固定的时间,例如 10 秒(相当于固定的 Δx\Delta xΔx),观察你能跑多远(相当于 Δy\Delta yΔy)。你跑得越远( Δy\Delta yΔy 越大),我们就认为你跑得越快。当然,也可以反过来:给定一个固定的距离,例如 100 米(相当于 Δy\Delta yΔy),你跑的时间越短( Δx\Delta xΔx 越小),我们就认为你跑得越快。
综合这两种情况,我们可以发现:无论是固定时间( Δx\Delta xΔx)还是固定距离( Δy\Delta yΔy),最终起决定作用的是 Δy\Delta yΔy 和 Δx\Delta xΔx 的比值 ΔyΔx\frac{\Delta y}{\Delta x}ΔxΔy。这个比值越大,你就跑得越快,对应的直线也就越陡。
因此,我们可以在直线上任意选取两个点,用它们纵坐标之差 Δy\Delta yΔy 与横坐标之差 Δx\Delta xΔx 的比值( ΔyΔx\frac{\Delta y}{\Delta x}ΔxΔy)来定义这条直线的斜率。
学过三角函数的同学也会知道,这个斜率恰好是该直线与 xxx 轴夹角 θ\thetaθ 的正切值 tanθ\tan \thetatanθ,即:
tanθ=ΔyΔx\tan \theta = \frac{\Delta y}{\Delta x} tanθ=ΔxΔy
也就是说,直线与 xxx 轴的夹角 θ\thetaθ 越大,其斜率就越大,倾斜得就越厉害,这与我们的经验是一致的。
06 曲线与切线
直线的情况较为简单,关键在于曲线。曲线与直线不同,它可以在某些地方较为平缓,而在另一些地方较为陡峭。因此,曲线在不同位置的倾斜程度是不同的。所以,我们不能简单地谈论“一条曲线”的倾斜程度(“斜率”),而只能说曲线在“某个具体点”的倾斜程度。
于是,我们需要引入一个新的概念:切线。

切线,直观地看,就是“刚好在这点‘碰到’曲线”的直线。由于切线是直线,因此切线具有斜率。于是,我们可以用切线的斜率来代表曲线在该点的倾斜程度。
传统上,我们可以这样定义切线:先随意画一条直线,使其与曲线有两个交点,这样的直线称为割线(仿佛把曲线“割断”了,如图中蓝色的 AB)。然后,让 B 点沿着曲线逐渐向 A 点靠近。直观上,当 B 点与 A 点重合时,割线 AB 就变成了曲线在 A 点的切线。
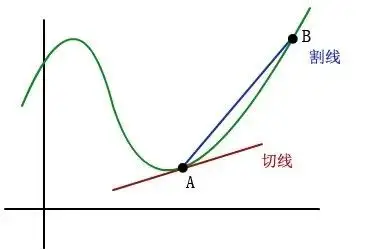
这种做法虽然符合人们的直觉,但在逻辑上存在一些问题:当 B 点向 A 点移动时,它究竟是在何时从割线变成切线的呢?
是在重合的时候吗?如果 B 点与 A 点重合,那么最后只剩下了一个点。我们知道“两点确定一条直线”,一个点怎么可能确定一条直线呢?然而,如果 B 点与 A 点不重合,那么这仍然是一条割线,而不是切线。
于是,这就出现了一个“一看非常简单直观,但是一说就说不清楚”的情况:似乎两个点不行,一个点也不行。那么,该如何解决呢?
解决这个问题有一个很朴素的思路:要确定这条切线,让 A、B 两点重合是不行的,但让它们分得太开也不行。最好的办法是让这两点无限靠近,但又不让它们重合。这样,既然是两个点,就可以确定一条直线;无限靠近又可以将其与一般的割线区分开来,这样不就两全其美了吗?
也就是说,A、B 两点必须无限靠近,但又不能重合。这样,它们的距离就无限接近于 0,但又不等于 0。这又是什么?这不就是无穷小吗?
在前面求曲线围成的面积时,核心思想是用无数个矩形去逼近原图形,这样每个矩形的底就变成了无穷小。在这里,我们又认为当 A、B 两点的距离变成无穷小时,割线 AB 就变成了过 A 点的切线。这似乎有些巧合,但它们之间的共性值得我们好好体会。
07 初见微分
利用无穷小定义了一点上的切线之后,我们就可以理所当然地用过该点的切线斜率来表示曲线在该点的倾斜程度。
如何求直线的斜率,我们前面已经介绍过。我们再回顾一下这张图:

直线的斜率等于直线上两点的纵坐标之差 Δy\Delta yΔy 与横坐标之差 Δx\Delta xΔx 的比值,即 ΔyΔx\frac{\Delta y}{\Delta x}ΔxΔy。
而切线是当曲线上 A、B 两点相隔无穷小时确定的直线,那么切线的斜率依然可以写成 ΔyΔx\frac{\Delta y}{\Delta x}ΔxΔy,只不过此时 Δx\Delta xΔx 和 Δy\Delta yΔy 都无限趋近于 0。
莱布尼茨给这两个趋近于 0 但又不等于 0 的 Δx\Delta xΔx 和 Δy\Delta yΔy 重新取了一个名字:dxdxdx 和 dydydy,并把它们称为“微分”。
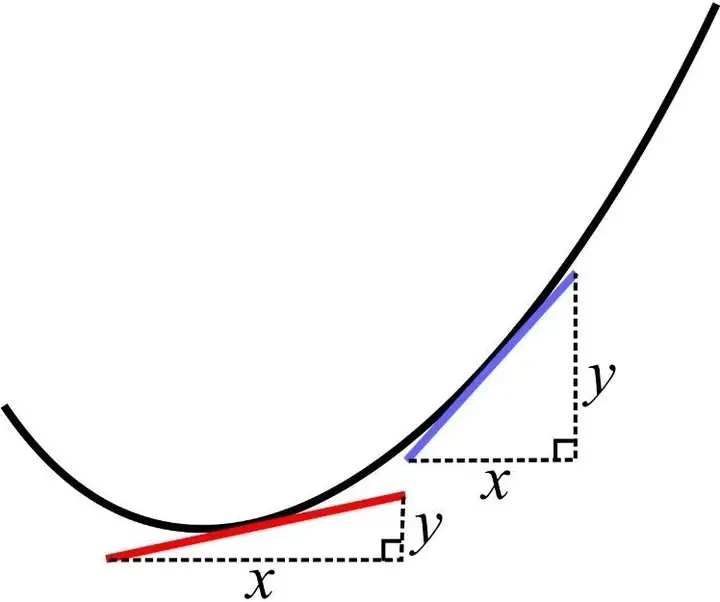
也就是说,对莱布尼茨而言,dxdxdx 这个微分就是当 Δx\Delta xΔx 趋向于 0 时的无穷小量,dydydy 亦然。虽然 dxdxdx 和 dydydy 都是无穷小,但它们的比值 dydx\frac{dy}{dx}dxdy 却是一个有限的数(此时就不能把无穷小 dxdxdx 当作 0 了,否则它还怎么当除数呢?),这就是该点切线的斜率。这样,一切似乎都解释得通了。
08 导数
显然,我们在曲线的一点上定义了切线,那么在平滑曲线的其他点上也可以定义切线。因为每条切线都有一个斜率,所以,曲线上的任何一点都有一个斜率值与之对应。两个量之间存在一种对应关系,这正是函数的定义。
函数 y=f(x)y = f(x)y=f(x) 告诉我们:给定一个 xxx,就有一个 yyy 与之对应。现在,我们是给定一个点(假设横坐标为 xxx),就有一个斜率 dydx\frac{dy}{dx}dxdy 与之对应。显然,这也是一个函数,这个函数被称为导函数,简称导数。
在中学阶段,我们通常在函数 f(x)f(x)f(x) 的右上角加上一撇来表示该函数的导数。因此,现在这两种情况都表示导数:
f′(x)=dydxf'(x) = \frac{dy}{dx} f′(x)=dxdy
所以,导数 f′(x)f'(x)f′(x) 可以表示横坐标为 xxx 的地方对应的切线斜率,它表示曲线在这一点上的倾斜程度。如果导数 f′(x)f'(x)f′(x) 的值较大,曲线就比较陡;如果 f′(x)f'(x)f′(x) 较小,曲线就比较平缓。因此,我们可以用导数来描述曲线的倾斜程度。
接下来,我们来看一个简单的例子,以了解如何实际求一个函数的导数。
例 1:求函数 f(x)=x2f(x) = x^2f(x)=x2 的导数。
这仍然是我们前面提到的抛物线,其函数图像如下:
求函数的导数,就是求函数在每一点的切线斜率。而切线是曲线上两个相距无穷小的点确定的直线。
假设曲线上有一个横坐标为 xxx 的点,那么与它距离无穷小的点的横坐标就是 x+dxx + dxx+dx。由于这个点也在曲线 f(x)=x2f(x) = x^2f(x)=x2 上,因此它的纵坐标为 (x+dx)2(x + dx)^2(x+dx)2,即:
f(x+dx)=(x+dx)2f(x + dx) = (x + dx)^2 f(x+dx)=(x+dx)2
然后,我们用这两个点的纵坐标之差 f(x+dx)−f(x)f(x + dx) - f(x)f(x+dx)−f(x) 除以横坐标之差 (x+dx)−x(x + dx) - x(x+dx)−x,就可以算出 xxx 点的切线斜率。因为 xxx 是任意取的,所以得到的结果就是任意点的切线斜率,也就是导数:
f′(x)=f(x+dx)−f(x)(x+dx)−x=(x+dx)2−x2dx=x2+2x⋅dx+(dx)2−x2dx=2x⋅dx+(dx)2dx\begin{aligned} {f}'(x) & =\frac{f(x+dx)-f(x)}{(x+dx)-x} \\ & =\frac{{{(x+dx)}^{2}}-{{x}^{2}}}{dx} \\ & =\frac{{{x}^{2}}+2x\cdot dx+{{(dx)}^{2}}-{{x}^{2}}}{dx} \\ & =\frac{2x\cdot dx+{{(dx)}^{2}}}{dx} \end{aligned} f′(x)=(x+dx)−xf(x+dx)−f(x)=dx(x+dx)2−x2=dxx2+2x⋅dx+(dx)2−x2=dx2x⋅dx+(dx)2
到这一步都很简单,接下来就出现了问题:分子和分母中的 dxdxdx 到底能不能约掉?
我们知道,除数不能为 0。如果想同时除以一个数,就必须保证这个数不是 0。现在我们想除以 dxdxdx,而 dxdxdx 是我们前面定义的无穷小量,它无限接近于 0,但又不等于 0。
因此,似乎可以姑且将其当作一个非零的量直接约掉。那么,导数上下同时除以 dxdxdx 就变成了:
f′(x)=2x⋅dx+(dx)2dx=2x+dxf'(x) = \frac{2x \cdot dx + (dx)^2}{dx} = 2x + dx f′(x)=dx2x⋅dx+(dx)2=2x+dx
这个式子看起来简洁了一些,但后面还是拖了一个小尾巴 dxdxdx。
2x2x2x 是一个有限的数,一个有限的数加上一个无穷小量,结果是多少呢?似乎应该等于这个具体的数。例如,100 加上一个无穷小,结果应该还是 100,因为如果等于 100.00…0001,那就不对了。无穷小肯定比你所有能给出的数还小,那么也肯定必须比 0.00…001 还小。
因此,我们似乎又有充足的理由把 2x2x2x 后面的这个 dxdxdx 也去掉,就像丢掉一个等于 0 的数一样。这样,最终的导数就可以简单地写成:
f′(x)=2xf'(x) = 2x f′(x)=2x
观察这个导数,当 xxx 越来越大( x>0x > 0x>0)时,f′(x)f'(x)f′(x) 的值也越来越大。而导数是用来表示函数的倾斜程度的,也就是说,当 xxx 越来越大时,曲线就越来越陡,这与图像完全一致。
然而,从逻辑上来看,这就有些奇怪了:一个无限趋近于 0 的无穷小量 dxdxdx 到底是不是 0?如果是 0,那么为什么可以让分子分母同时除以它来约分?如果不是 0,那么为什么又可以将其随意舍弃呢?
总不能同时等于零又不等于零吧?你又不是薛定谔家的无穷小量。

数学不是变戏法,不能如此随意。因此,这个无穷小量再次招致了许多批判。为什么说是“再次”呢?因为在前面讲积分时已经提到过一次,而在这里体现得更加明显。第二次数学危机似乎已经迫在眉睫。
09 导数的意义
经过前面的详细阐述,我们从直线的斜率讲到了曲线的导数,这已经进入了微分学的核心领域。那么,导数为何如此重要呢?
因为导数反映的是一个量变化快慢的程度,这实际上是一种广义的“速度”。速度在科学中的重要性不言而喻。当我们说一辆车的速度很快时,实际上是在说这辆车的位移对时间的导数很大。
此外,有了导数,我们就可以轻松地求一条曲线的极值(极大值或极小值)。为什么呢?因为只要导数不为 0,曲线在这里就是在上升(大于 0)或者下降(小于 0)。只有导数等于 0 的地方,才有可能是一个极值点。
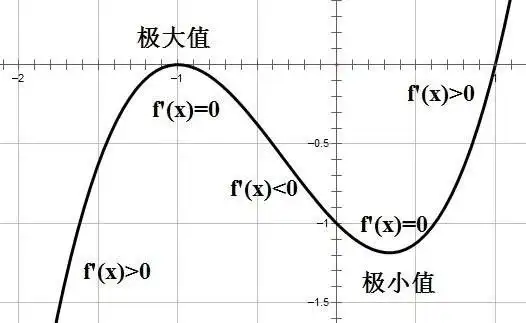
求极值是非常重要的。军人希望他们发射的炮弹可以飞得尽可能远;商人希望他们的利润可以尽可能高;我们也希望去任何地方都能走最近的路。
导数的这些应用很多人都知道。事实上,前面提到的求曲线围成的面积以及求曲线的导数等内容,在牛顿和莱布尼茨之前就已经被人们所熟知。然而,这些并不是最重要的。
牛顿和莱布尼茨之所以伟大,之所以被尊称为微积分的发明人,是因为他们在这些看似平常的事实背后发现了一个极为不寻常的秘密:求面积和求导数,或者说积分和微分,这两个看似完全不相关的运算,竟然是一对互逆的运算。

在此,我们不妨暂停片刻,仔细思考一下这句话,体会一下这一极为重要的发现所带来的震撼。
10 互逆运算
积分和微分是一对互逆运算,这是微积分最核心的思想。将这一思想用数学语言描述,便形成了一个定理,即微积分基本定理。
这一发现是牛顿和莱布尼茨在微积分领域最重要的贡献,因此,微积分基本定理又被称为牛顿-莱布尼茨公式。一个定理能够被冠以“XX基本定理”之名,且由该领域的两位发明者直接冠名,其重要性不言而喻。
那么,“积分和微分是互逆运算”究竟意味着什么?“互逆运算”的定义是什么?为何这一发现如此重要?下文将逐步阐释。
互逆运算,从直观上理解,指的是存在两种运算,其中一种运算可将某个对象“变过去”,而另一种运算能将其“变回来”。
最常见的互逆运算便是加法和减法:3+2=53 + 2 = 53+2=5,5−2=35 - 2 = 35−2=3。3 加上 2 得到 5,反过来,5 减去 2 又能变回 3,因此加法和减法是一对互逆运算,这易于理解。

当我们说“求面积(积分)和求导(微分)是一对互逆运算”时,意思是:若对某个对象进行积分操作(求面积)得到一个新对象,再对这个新对象进行微分操作(求导),能够得到原来的对象,这样的两种运算才称得上互逆。
下面通过一个简单例子,直观感受积分和微分的互逆关系。
假设从家到学校需要走10 分钟,将这 10 分钟平均分成10 份,每份1 分钟。那么,第1分钟内行走的距离等于第1分钟的平均速度乘以时间间隔(1 分钟),第2分钟内行走的距离等于第 2 分钟的平均速度乘以时间间隔(1 分钟)。以此类推,将这 10 个 1 分钟内行走的距离相加,结果便是家到学校的总距离,这一点不难理解。

这一过程实际上就是积分。前文在求曲线围成的面积时,是将曲线围成部分的**xxx 轴平均分成多个矩形**,再将每个矩形的面积相加。此处求家到学校的总距离,同样是将家到学校的时间平均分成多份,然后把每个小份的距离相加。
两者都是将一个整体(家到学校的总距离,曲线围成的总面积)平均分割成多个部分,每个部分用一个新的量(每一分钟的距离,每一个矩形的面积)近似,最后将所有部分的量相加,以逼近原来的整体。
求面积时,矩形数量越多,面积之和就越接近真实面积。同样,将家到学校的 10 分钟分得越细(例子中仅分了 10 份,还可分为 100 份、1000 份甚至更多),得到的总距离就越精确。
此外,时间段分得越细,每个小时间段内的平均速度就越接近瞬时速度;若无穷细分,那么无穷小时间段内的平均速度可视为瞬时速度。
也就是说,若已知整个过程中的瞬时速度(或无穷小时间段内的速度),就能精确求出无穷小时间段内的距离,再将所有距离相加,得到精确的总距离,这就是积分。即通过积分,能从瞬时速度求出总距离。
另一方面,要证明微分(求导) 是这一过程的逆运算,需证明从总距离可以求出瞬时速度。即若已知任意时刻从家到学校的距离,通过微分(求导)能得到瞬时速度。
这是显而易见的:距离对时间求导的结果就是速度,前文也提到“导数是一种广义的速度”。距离除以时间,结果为速度。用平均距离除以平均时间得到平均速度,用瞬时距离(某一时刻的距离)除以瞬时时间(无穷小时间片段)自然得到瞬时速度。因此,通过积分能从瞬时速度求出总距离,通过微分能从总距离求出瞬时速度,这表明积分和微分是一对互逆运算。也可从图像角度更直观地理解这一点。
11 v-t 图像
中学物理中,老师一定会绘制速度-时间(v-t) 图像。v-t 图像是在坐标系中,以纵轴表示物体运动的速度 vvv,横轴表示时间 ttt,进而分析物体的运动情况。如下图:
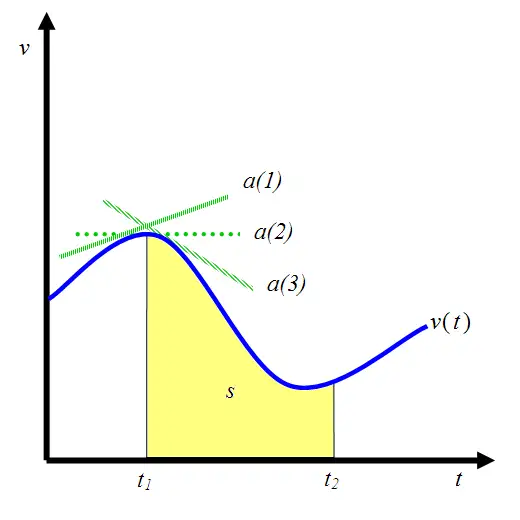
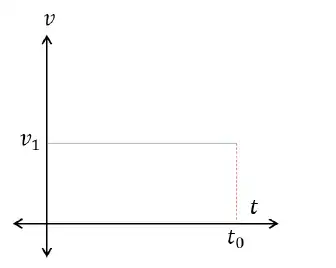
老师会告知:v-t 图像中围成的面积 sss 就是物体运动的位移大小(位移是有方向的距离,属于矢量)。该坐标系中,横轴为时间 ttt,纵轴为速度 vvv,计算面积需用到乘法。物体做匀速运动的轨迹是一条平行于**ttt 轴的直线,速度 v1v_1v1乘以时间 t0t_0t0 即为所围成矩形的面积 sss,而速度乘以时间的物理意义就是位移**。因此,面积代表位移,十分合理。
当物体做非匀速运动(轨迹为曲线)时,可将时间切割成多个小段,在每一小段内近似当作匀速运动,则每一小段的面积代表该小段内的位移。
将所有小段的面积相加,得到的总面积即可代表总位移。因此,曲线围成的面积 sss 同样代表位移。
处理曲线时,将时间分割成多块,用每一块的面积(位移)之和逼近总面积(位移),这正是积分的思想。反过来,若将黄色的面积 SSS(即整体的位移)看作随时间 ttt 变化的函数,对其求导可得到速度 vvv。即对速度 vvv 进行一次积分能得到位移 sss;反过来,对位移 sss 求一次导数(微分) 能得到速度 vvv。二者的互逆关系清晰可见:
s=∫0tv(t′)dt′和v(t)=dsdts = \int_{0}^{t} v(t') \, dt' \quad \text{和} \quad v(t) = \frac{ds}{dt}s=∫0tv(t′)dt′和v(t)=dtds
这部分逻辑不难理解,只要仔细思考,便会发现“积分和微分是互逆运算”是非常自然的结论,在日常生活中随处可见,只是牛顿和莱布尼茨率先发现了这一点。
12 原函数
“积分和微分是互逆运算”这一发现能带来什么?答案是:多一种解决问题的选择。由于积分和微分互为逆运算,当积分在某些操作中不占优势时,可借助微分来解决。
以最初求曲线围成的面积为例。求抛物线**y=x2y = x^2y=x2与 x 轴在 0 到 1 之间围成的面积时,若用nnn个矩形逼近,每个矩形的底为1/n1/n1/n,则 n 个矩形的面积之和**为:
S=∑i=1n(in)2⋅1nS = \sum_{i=1}^{n} \left( \frac{i}{n} \right)^2 \cdot \frac{1}{n}S=i=1∑n(ni)2⋅n1
当 nnn 趋向于无穷大时,后两项为无穷小,结果仅剩第一项**1/31/31/3**。
这种方法针对不同曲线需使用不同求和公式,且需保证相关项可变为无穷小而舍去,因此复杂度和局限性极大,难以推广。
但在牛顿和莱布尼茨发现“积分和微分是互逆运算”后,情况发生了改变。我们有了另一种选择:若积分之路困难,可转而借助微分。
具体怎么做呢?前文讲微分时,计算过**f(x)=x2f(x) = x^2f(x)=x2的导数**,结果为:
f′(x)=2xf'(x) = 2xf′(x)=2x
那么,若已知函数为**f(x)=2xf(x) = 2xf(x)=2x,能否反推出哪个函数求导后得到f(x)=2xf(x) = 2xf(x)=2x?显然可以,不难推出原来的函数是f(x)=x2+cf(x) = x^2 + cf(x)=x2+c**。
这里多出一个常数 ccc,是因为常数的导数均为 0。
即 f(x)=x2f(x) = x^2f(x)=x2、f(x)=x2+1f(x) = x^2 + 1f(x)=x2+1、f(x)=x2+3f(x) = x^2 + 3f(x)=x2+3 等函数的导数都是 f(x)=2xf(x) = 2xf(x)=2x,仅根据 f(x)=2xf(x) = 2xf(x)=2x 无法确定最初的函数具体形式,但可确定其必定是 x2x^2x2 加上一个常数 ccc。于是,求导之前原来的函数 f(x)=x2+cf(x) = x^2 + cf(x)=x2+c 被称为 f(x)=2xf(x) = 2xf(x)=2x 的原函数。
关键在于:积分是求函数围成面积的过程,速度 vvv 通过积分得到位移 sss,在v-t 图像中速度 vvv 围成的面积即为位移 sss;微分是求导的过程,对位移 sss 求一次导数可得到速度 vvv。
有了原函数后,可根据速度 vvv求出(求导后等于速度 vvv 的)位移 sss,此时位移 sss 就是速度 vvv 的原函数(再加一个常数 ccc)。而原函数表示的位移 sss 是速度 vvv 围成的面积,因此,原函数具有求面积(积分)的效果。
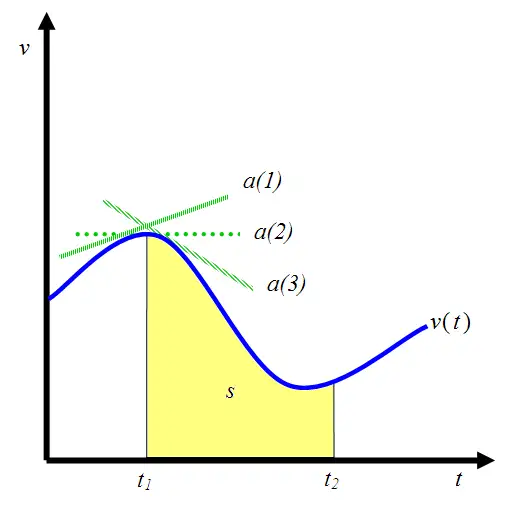
即 sss** 求导一次得到 vvv,那么 vvv 反向求导一次可得到 sss,此时 sss 是 vvv 的原函数**。另一方面,因 sss求导一次得到 vvv,所以 vvv 积分一次也能得到 sss(互逆运算)。因此,vvv 通过求原函数和积分都能得到 sss,原函数 sss 具有积分(曲线 vvv 围成面积)的效果。
简言之,由于积分和微分是互逆运算,反向微分(求原函数) 可“负负得正”,达到与积分相同的效果。
因此,求曲线 f(x)=x2f(x) = x^2f(x)=x2 和 xxx 轴在 0 到 1 区间内围成面积这一原本属于积分的问题,如今可通过反向微分(求原函数) 解决。
这一转变意义重大,能极大简化问题,也使数学发生了根本性变革。
13 微积分基本定理
既然要用反向微分的方法求面积,就需找到 f(x)=x2f(x) = x^2f(x)=x2 的原函数,即求导后结果为 f(x)=x2f(x) = x^2f(x)=x2 的函数。用 F(x)F(x)F(x) 表示该原函数,则有(CCC 为常数):
F(x)=13x3+CF(x) = \frac{1}{3}x^3 + CF(x)=31x3+C
可自行验算,该 F(x)F(x)F(x) 求导后的结果确实为 f(x)=x2f(x) = x^2f(x)=x2。
由于求导是基础且重要的运算,常见函数的导数和原函数已被整理成表格,使用时可直接查阅,同时需记住常用的部分。不过,学习初期仍需亲自计算一些求导例子。
有了 f(x)=x2f(x) = x^2f(x)=x2的原函数 F(x)F(x)F(x)后,如何求 f(x)f(x)f(x)和 xxx 轴在0到1区间内围成的面积?如前所述,原函数具有积分的效果,而积分即曲线围成的面积,因此原函数可表示曲线围成的面积(为便于理解,暂不考虑**常数 CCC**的影响,因其在函数相减时会抵消)。
因此,求 f(x)f(x)f(x) 与 xxx 轴在 0 到 1 区间内围成的面积,直接用代表面积的原函数 F(x)F(x)F(x) 在 1 处的值 F(1)F(1)F(1) 减去在 0 处的值 F(0)F(0)F(0) 即可:
面积=F(1)−F(0)=(13×13+C)−(13×03+C)=13\text{面积} = F(1) - F(0) = \left( \frac{1}{3} \times 1^3 + C \right) - \left( \frac{1}{3} \times 0^3 + C \right) = \frac{1}{3}面积=F(1)−F(0)=(31×13+C)−(31×03+C)=31
结果为 1/31/31/3,与用矩形逼近计算的结果一致,且该方法简便得多,这正是微积分的力量所在。
基于上述铺垫,微积分基本定理(牛顿-莱布尼茨公式)易于理解:若函数 f(x)f(x)f(x) 在区间 aaa 到 bbb 上连续(简单理解为曲线不间断),且存在原函数 F(x)F(x)F(x),则有:
∫abf(x)dx=F(b)−F(a)\int_{a}^{b} f(x) \, dx = F(b) - F(a)∫abf(x)dx=F(b)−F(a)
式子左边是函数 f(x)f(x)f(x) 与 xxx 轴在 aaa 到 bbb 区间内围成的面积,前文讲积分时已提及:

式子右边是原函数在 bbb 点和 aaa 点的差值。其意义明确:通过反向求导得到的原函数 F(x)F(x)F(x)本就表示面积,那么 F(b)−F(a)F(b)-F(a)F(b)−F(a) 自然是这两点之间的面积之差。因此,公式左右两边均表示面积,逻辑自洽。
这便是微积分的基本定理和核心思想。

牛顿和莱布尼茨发明微积分的本质,在于他们发现“积分和微分是一对互逆运算”,进而可采用“反向微分(求原函数)”的方法处理积分问题。
积分的逆运算是微分,对微分进行再逆运算,便“负负得正”,回到积分。而“对函数求导、求原函数”比用原始定义(无穷多个矩形逼近曲线面积)简便得多,且具有一般性。
因此,原本独立的积分和微分,经牛顿和莱布尼茨统一为微积分,产生了远超两者单独作用的力量,推动了后续数学和科学的空前发展。
14 数学的力量
微积分的发明极大降低了求曲线围成面积的难度。这一过程中,数学为何能有效简化问题?是问题本身简单却被复杂化,还是问题的复杂度确实被降低了?
以小学的“鸡兔同笼”问题为例:鸡和兔关在一个笼子里,从上数有 35 个头,从下数有 94 只脚,求笼中鸡和兔的数量。

有些老师会教授特殊解题技巧:鸡有 1 个头2只脚,兔有 1 个头4只脚,总共有 35 个头,将 35 乘以 2 得 70,即所有鸡的脚加一半兔子的脚(因兔有 4 只脚,仅乘 2,每只兔还有 2 只脚未算)。
用总脚数 94 减去 70 得24,即剩下的一半兔子脚,再用 24 除以2(一只兔 4 只脚,一半为2只),得到兔子数量 12。总共有 35 个头,故鸡的数量为 35 - 12 =23。
“鸡兔同笼”问题还有其他特殊解法,但这些解法存在明显局限:仅适用于鸡和兔的情况,若换成其他动物或数的是翅膀和脚,便不再适用。
这与阿基米德用穷竭法求曲线围成的面积类似,每种曲线对应的面积求法不同,解法严重依赖曲线的具体特性,因此局限性大,意义有限。而微积分的伟大之处在于,它从看似不同的问题中抽象出共同本质,使所有问题都可套用同一套程序解决,为后续发展奠定了基础。
学习方程后,会发现“鸡兔同笼”问题变得简单,且无论问题如何变化(加入其他动物、数翅膀等),都可按相同程序解决。原因何在?
没有方程时,需具体问题具体分析,进行逆向分析。
逆向思考本身不符合人类的常规思维方式。从一系列原因推出结果较为容易,但从结果反推原因则困难得多(这也是侦探职业存在的原因)。

例如,已知有 23 只鸡和 12 只兔,计算头和脚的数量是正向思维,较为容易;但已知头和脚的数量,反推鸡和兔的数量则是逆向思维,较为麻烦。
方程提供了一种思路:为何不用熟悉的正向思维,而采用麻烦的逆向思维?即使不知道鸡和兔的数量,可用未知量代替,先通过正向思维列出方程。
假设鸡有 xxx 只,兔有 yyy 只,则总共有**x+yx + yx+y个头,2x+4y2x + 4y2x+4y**只腿。根据题目条件,可列出:
{x+y=352x+4y=94\begin{cases}x + y = 35\\2x + 4y = 94\end{cases}{x+y=352x+4y=94
列出这两个方程后,问题基本解决,剩下的便是求解 xxx 和 yyy,而解方程是高度程序化的过程,不同方程的求解都有固定方法。
从小学的“聪明技巧”到程序化地列方程、解方程,这是数学上的显著进步。需思考:这一过程中发生了什么?方程如何简化问题?这与微积分的发明有何相似之处?
实际上,之前思考“鸡兔同笼”问题时的逆向思维过程,已被整合到解方程的步骤中。
以解上述方程为例:
{x+y=352x+4y=94\begin{cases}x + y = 35\\2x + 4y = 94\end{cases}{x+y=352x+4y=94
老师可能会教授固定方法:
第一步,将方程 1 两边都乘以 2,得到**2x+2y=702x + 2y = 702x+2y=70**(与前文将所有鸡兔的头乘以 2 的思路一致)。
第二步,用方程 2 减去方程 1,消去 xxx,得到**2y=242y = 242y=24(与前文用脚的数量减去 2 倍头的数量得到兔子剩下的脚的一半思路相同),进而求出兔子的数量y=12y = 12y=12**。
第三步,将 y=12y = 12y=12 代入方程 1,求出 xxx 的值,得到鸡的数量 23。
可见,之前思考问题时的复杂步骤,如今已被机械化地纳入解方程过程。曾经认为的巧妙解题技巧,不过是最简单的解方程方法,因此问题变得简单。
这就是数学的作用!
数学不断从不同领域抽象出相同本质,并尽可能将抽象内容一般化、程序化,使人们能更便捷地掌握各种高级数学工具。
因此,数学的发展趋势是越来越抽象,更注重一般化、程序化解决问题的方法。方程思想具有革命性,微积分亦是如此。
微积分采用通用方法处理各种曲线围成的面积,稍作变化便可求出曲线的长度或曲面的体积。微积分简化求面积逻辑的原因在于,它将这部分逻辑整合到求原函数中,而求原函数是可程序化、一般化的操作。
学习数学时,应更多关注数学从不同领域抽象出的相同本质,以及如何一般化地解决这类问题。这是数学的“核心”,无需过于在意小技巧,不必耗费时间琢磨“鸡兔同笼”问题的多种解法,以免本末倒置。
这段内容虽看似偏离主题,但对于理解数学的定位、学习数学的方法以及微积分的意义都大有裨益。否则,学了十几年数学却不知数学为何物,将是极大的遗憾。
15 进击的微积分
微积分已创立,其基本定理也已提出,但这并非终点,后续还有大量工作要做。
微积分基本定理的核心是通过求原函数解决求面积问题,因此求函数的原函数成为核心问题。为此,需研究各种常见函数的求导和求原函数方法。
明确这些后,还需探究:由常见函数组成的复合函数(如相加减、相乘除、相嵌套复合等)如何求原函数和积分?进一步扩展,已知如何求面积,那么如何求体积和曲线的长度?
这部分内容是学习的重点,也是考试的核心,需熟悉前人总结的微积分技巧,通过大量练习掌握,没有捷径。但需警惕将微积分学习仅视为技巧训练,否则数学将沦为算术。
此外,建议有追求的同学不要急于翻阅课本寻找答案。前文已阐述微积分的思想,可尝试独立推导这些问题,实在无法解决再查阅课本,正如孔子所说“不愤不启,不悱不发”。
像牛顿和莱布尼茨那样洞察“积分和微分是互逆运算”并提出微积分基本定理,是一流科学家的素养。在一流科学家提出重大创新后,能完善后续相关内容,是二流科学家的基本素养。学习数学时,应有意识地培养这种能力。
随后,可将微积分技术扩展到其他领域。例如,利用微积分研究曲线、曲面等弯曲的对象,形成微分几何,这在后续讲解广义相对论时必不可少。
借助微积分,许多物理定律可表示为微分方程,多变量时则为偏微分方程。前文提到的麦克斯韦方程组、波动方程,以及后续将讲解的广义相对论的场方程均是如此。
有了微积分,可计算各种曲线的长度,进而研究特定条件下最短曲线的确定方法,由此发展出变分法。变分法与最小作用量原理相结合,在物理学发展中发挥了关键作用。

因此,微积分在接下来的两个世纪中迅速发展。科学(尤其是物理学)的发展需要微积分,微积分也从科学中汲取养分,二者相互促进、共同成长。
16 被忽略的无穷小
但是,似乎大家都忘了一个问题:此时微积分的基础并不牢固,莱布尼茨把 dxdxdx 视为一个无穷小量,但是无穷小量还是怎么说都说不圆。
一个接近于 0 又不等于 0 的无穷小量到底是个什么玩意?为什么你有时候可以把它当除数约掉(认为它不为 0),有时候又随意把它舍弃(认为它等于 0)?看数学史的时候也会觉得奇怪,像欧拉、拉格朗日、拉普拉斯、伯努利兄弟这些顶级数学家,居然都对这些问题视而不见。更让人奇怪的是,他们使用这种逻辑不严密的微积分居然没有出什么差错,只能说大佬们的直觉确实逆天。
因此,微积分最后的问题就是:如何使微积分严密化?如何把微积分建立在一个坚实的基础之上?
之所以把**dxdxdx看成一个无限趋近于 0 却又不等于 0 的无穷小量**,主要是因为这样做很直观。我们用很多矩形去逼近曲线围成的面积,矩形数量越多,每个矩形的宽度就越小。当矩形的数量变成“无穷多个”的时候,每个矩形的宽度就“理所当然”地变成了无穷小。这么看,无穷小量确实很直观,但是这里有什么问题呢?
当我说矩形的数量是一百个、一千个的时候,我是可以把它们都数出来的,我也可以把它们的面积之和都算出来。但是,当你说矩形的数量是无穷多个的时候,无穷多个是多少个?你能数出来么?你真的可以把无穷多个矩形的面积一一算出来,然后把它们加起来么?
有人可能觉得我在胡搅蛮缠。无穷嘛,那肯定是无法具体数出来、测出来的,也不可能真的把无穷多个矩形的面积一个个算出来再求和。但是我知道是那么个意思,是那么回事就行了。我测不出来,但是我能想出来,难道还不让我想了么?
对,还真就不让想了!
大家可能都知道,科学和哲学以前是一家的。因为纯粹的思辨在哲学里非常常见,所以以前的“科学”里就到处夹杂着这种“可以想但是无法测量的东西”,这就极大的限制了科学的发展。因为一个东西如果无法测量你就无法用实验去验证它,无法验证你就不知道它是对是错,你不知道对错那就只能以权威说了算。你没有证据还敢说权威不对,那就很麻烦了,所以亚里士多德的学说可以统治欧洲近两千年。
现代科学从哲学里分离了出来,一个标志性的操作就是:科学家们开始关注那些能够用实验测量到的量,对那些用实验无法测量的东西避而不谈。
伽利略是公认的“现代科学之父”,他的核心观点有两条:第一,用数学定量地描述科学;第二,用实验验证科学。所以,如果你谈的是现代科学,那你就不能乱想了。
如果你还想用一些无法测量的概念来构建你的“科学体系”,那么你的方法论就是非科学的,你构建的也只是玄学而非科学,这是很多民科非常容易犯的错误。庞加莱甚至直接说:“凡是不能测量的东西,都不能算是自然科学。”

这种思想在科学昌盛的 19 世纪已经很普遍了,诞生于这个时期的实证主义也指出:人类不可能也不必要去认识事物的“本质”,科学是对经验的描写。他们甚至提出口号要“取消形而上学”。
17 柯西来了
总之,一切的一切就是不让你在科学里再谈那些无法测量,无法验证的概念,科学要基于实证。
那么,只能想却无法数,无法“观测”的无穷小量是不是这样的一个概念呢?虽然它很直观,但是你回顾科学的历史,反直觉的重大科学进步难道还少么?历史一次次地告诫我们:直觉不可靠,我们能依靠的只有严密的逻辑和确凿的实验。
在这样的大环境下,我们迎来了一位重要人物:柯西。

柯西深刻地认识到:只要涉及数学概念,任何关于连续运动的一些先验的直观观念,都是可以避免,甚至是必须避免的。科学放弃了形而上学方面的努力,采用“可观测”概念之后就迎来了大发展,那数学为什么不也这样呢?
无穷小量是一个无限趋近于 0 但是又不能等于 0 的概念,也就是说它有一个极限位置 0,你可以想多接近就多接近,但就是无法到达。
我们知道实数跟数轴上的点是一一对应的。 当我们说一个量在无限趋近于 0 的时候,很多人脑海里浮现的画面就是一个点在数轴上不停地移动,从一个点移动到下一个点,一直靠近 0 这个点。
但是这个图景是不对的,为什么?因为实数是稠密的。稠密就是说任意两个点(实数)之间永远都有无数个点(实数)(你自己想想是不是,1 和 2 之间有多少个数?)。你以为它能从 A 点移动到邻近的下一个 B 点么?对不起,这个它真做不到!
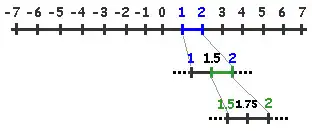
A 点和 B 点之间永远有无数个点,也就是说A 点根本就没有所谓的“下一个点”。 你认为我一定要走完了 A 点到 B 点之间所有的点才能到达 B 点,那就不可避免地会陷入到芝诺悖论里去。因为你压根就不可能走完任何两个点之间的所有点(因为是无穷多个),所以,如果按照这种逻辑,你就根本“走不动”,所以芝诺的飞矢就飞不动了。
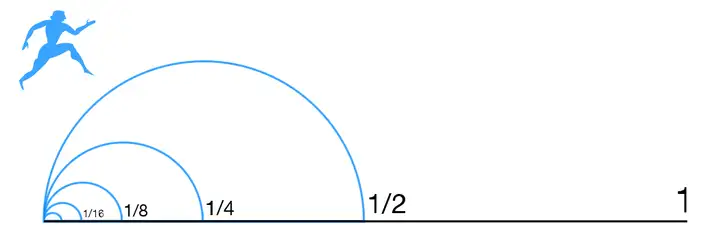
因此,面对这种连续的概念的时候,我们就不应该使用这种“动态的”定义。你想通过“让一个点在数轴上动态地运动来定义极限”是行不通的,这就是莱布尼茨的无穷小量栽跟头的真正原因。
数学家们经过一百多年的探索、失败和总结,最后终于意识到了这点,这些思想在柯西这里完全成熟。于是,柯西完全放弃了那种动态的定义方式,转而采取了一种完全静态,完全可以描述测量的方式重新定义了极限,进而为微积分奠定了扎实的基础。
这里我把柯西对极限的新定义原封不动的贴出来:当一个变量相继的值无限地趋近某个固定值的时候,如果它同这个固定值之间的差可以随意地小,那么这个固定值就被称为它的极限。
有人看了这个定义之后就在犯嘀咕:这跟莱布尼茨说的不是一样的么?你还不是在用“无限趋近”啊,“随意的小”啊这种跟“无穷小”差不多的概念来定义极限么?你说以前的定义是动态的,柯西给整成了静态的,可是我看来看去,柯西这个定义好像也在动啊。什么无限趋近,随意的小,不是在动么?
有这些疑问是正常的,毕竟是让数学家们卡了一百多年的问题,不可能那么太“显而易见”。
我们再仔细看看柯西的定义,它跟以前的差别到底在哪?你看啊,柯西虽然也有用“无限趋近”,但是他只是用这个来描述这个现象,并不是用它来做判决的。他的核心判决是后面一句:如果它同这个固定值之间的差可以随意的小,那么它就是极限。
可以随意的小和你主动去无限逼近是完全不一样的。可以随意小的意思是:你让我多小我就可以多小。你让我小于 0.1,我就能小于 0.1;你让我小于 0.01,我就能小于 0.01;你让我小于 0.00…001,我就可以小于 0.00…001。只要你能说出一个确定的值,不管你说的值有多小,我都可以让它跟这个固定值的差比你更小。柯西说如果这样的话,那么这个固定值就是它的极限。
大家发现没有,柯西学聪明,学鸡贼了,他把这个判断过程给颠倒了过来。以前是你要证明自己的极限是 0,你就不停地变小,不停地朝 0 这个地方跑过去。但是,你和 0 之间永远隔着无数个点,所以你永远也跑不完,你也就不知道你要跑到什么时候去,这样就晕了。
现在我学聪明了,这个难以界定的东西,这个烫手的山芋我不管了,我丢给你,我让你先说。只要你说出一个数,你要我变得多小我就变得多小。你如果想让我变成无穷小,那你就得先把无穷小是多少给我说出来,你说不出来的话那就不能怪我了。

完美甩锅!这就是柯西的核心思想。
柯西就通过这种方式把那些不可测的概念挡在了数学之外,因为你能具体说出来的数,那肯定就都是“可观测”的啊。大家再看看这个定义,再想想之前莱布尼茨的想法,是不是这么回事?
于是,柯西就这样完美的甩开了那个招人烦的无穷小量。在柯西这里,无穷小量不过就是一个简单的极限为 0 的量而已,一个“只要你可以说出一个数,我肯定就可以让我和 0 之间的差比你给的数更小”的量。这样我们就能把它说得清清楚楚,它也不再有任何神秘了。
18 魏尔斯特拉斯和ε-δ极限
然后,魏尔斯特拉斯用完全数学的语言改进了柯西的这段纯文字的定义,得到了最终的,也是我们现在教材里使用的ε-δ 极限定义。
根据柯西的思想,魏尔斯特拉斯说:你要判断某个函数 f(x)f(x)f(x)在某个地方 aaa的极限是不是某个值 LLL,关键就要看如果我任意说一个数 ε\varepsilonε(比如 0.00…001 或者任意其它的,注意是任意取,这里用 ε\varepsilonε 代替),你能不能找到一个 xxx 的取值范围(用 Δ\DeltaΔ来衡量),让这个范围里的函数值 f(x)f(x)f(x) 与那个值 LLL之间的差(用套个绝对值的 |f(x)-L| 表示)小于 ε\varepsilonε。如果你总能找到这样的 Δ\DeltaΔ,那我就说函数 f(x)f(x)f(x) 在 aaa 点的极限为 LLL。
用精练的数学语言表述上面的话就是:当且仅当对于任意的 ε\varepsilonε,存在一个 δ>0\delta>0δ>0,使得只要 0<∣x−a∣<δ0<|x-a|<\delta0<∣x−a∣<δ,就有 ∣f(x)−L∣<ε|f(x)-L|<\varepsilon∣f(x)−L∣<ε,那么我们就说 f(x)f(x)f(x) 在 aaa 点的极限为 LLL。记做:
limx→af(x)=L\lim_{x \to a}f(x) = Lx→alimf(x)=L
定义里的Lim就是极限的英文单词Limit的缩写,这个箭头**x−>ax->ax−>a**也非常形象地表达了极限这个概念。
这个定义就真正做到了完全“静态”,不再有任何运动的痕迹(连柯西说的“无限趋近”、“随意的小”都没有了),也不再有任何说不清的地方。从定义你也能清楚地看出来:它根本不关心你是如何逼近 LLL 的,飞过去、跳过去、爬过去的它都不管,只要最后的差比 ε\varepsilonε 小就行,我就承认你是我的极限。
用一位伟人的名言翻译一下就是:不管黑猫白猫,能比 ε\varepsilonε 还小的就是我的极限好猫。

这里要特别注意的是 ε\varepsilonε 是任意的,任意就是说随便 ε\varepsilonε 取什么你都要找到对应的 Δ\DeltaΔ,你不能说有 10 个 ε\varepsilonε 满足条件就说这是极限。
看个例子,我们考虑最简单的 f(x)=1/xf(x)=1/xf(x)=1/x。当 xxx 的取值(x>0x>0x>0)越来越大的时候,这个函数的值就会越来越小:f(1)=1f(1)=1f(1)=1,f(10)=0.1f(10)=0.1f(10)=0.1,f(100)=0.01f(100)=0.01f(100)=0.01,f(1000)=0.001f(1000)=0.001f(1000)=0.001,……
看得出来,当 xxx 的取值越来越大的时候,f(x)f(x)f(x) 的值会越来越趋近于 0。所以,函数 f(x)f(x)f(x) 在无穷远处的极限值应该是 0,也就是说:
limx→+∞1x=0\lim_{x \to +\infty}\frac{1}{x} = 0x→+∞limx1=0
这个结论是很明显的,接下来我们就来看看如何用 ε-δ 定义来说这个事。
按照定义,我们要取一个任意小的 ε\varepsilonε,假设这里我们取 ε=0.1\varepsilon=0.1ε=0.1,那么我们就要去找一个 Δ\DeltaΔ,看能不能找到一个范围让 ∣f(x)−0∣<0.1|f(x)-0|<0.1∣f(x)−0∣<0.1,显然只需要 x>10x>10x>10 就行了;取 ε=0.01\varepsilon=0.01ε=0.01,就只需要 x>100x>100x>100 就行了;任意给一个 ε\varepsilonε,我们显然都能找到一个数,当 xxx 大于这个数的时候满足 ∣f(x)−0∣<ε|f(x)-0|<\varepsilon∣f(x)−0∣<ε,这样就 OK 了。
于是,我们就构建了一个逻辑严密,不再有任何“说不清”概念的极限理论。有了这个坚实的地基,我们就可以放心地在上面盖房子了。那个漂泊了一百多年,那个被幽灵般的无穷小量缠绕了一百多年的微积分,即将迎来新生。
19 积分的重建
先看积分,我们之前认为曲线围成的面积是无数个宽度为无穷小量的矩形面积之和,于是我们在这里就被无穷小量缠上了。有了 ε-δ 极限之后,我们就可以刷新一下我们对积分的认知了:从现在起,我们把曲线围成的面积看成是一个极限,而不再是无数个无穷小量的矩形面积之和。
什么意思?假设我们用 1 个矩形逼近曲线围成的面积的时候,我把这一个矩形的面积记做**S1S_1S1**,用两个矩形逼近的面积之和记做 S2S_2S2,同样的,我们记下 S3,S4,S5S_3,S_4,S_5S3,S4,S5……
一般情况,如果我们用 nnn 个矩形去逼近这个面积,这 nnn 个矩形的面积之和就记做 SnS_nSn。如果这个 SnS_nSn 的极限存在,也就是说,随便你说出一个数字 ε\varepsilonε,我都能找到一个 nnn 的范围,让 SnS_nSn 和 AAA 之间的差 |S_n-A| 小于你给定的这个数字 ε\varepsilonε。那么,AAA 就是这个 SnS_nSn 的极限。
Sn→A\mathop{S}_{n}\to ASn→A
于是,我们就说:曲线围成的面积就是这个极限 AAA,它是 nnn 个矩形面积之和这个序列 SnS_nSn 的极限。
所以,我们就把这个极限过程表示的面积 AAA定义为函数 f(x)f(x)f(x)从 aaa 到 bbb 上的积分:
∫abf(x)dx=limn→+∞∑i=1nf(xi)Δx\int_{a}^{b}f(x)dx=\lim_{n \to +\infty}\sum_{i = 1}^{n}f(x_i)\Delta x∫abf(x)dx=n→+∞limi=1∑nf(xi)Δx
这样,我们的积分就成了一个由 ε-δ 语言精确定义的极限。这里没有那个等于 0 又不等于 0 的无穷小量,一切都清清楚楚、明明白白,没有含糊的地方,这就是第二次数学危机的终极解决之道。
这样处理虽然不再那么直观,但是它非常精确和严密,这是符合数学的精神的。直观虽然能帮助我们更好的感受数学,但是如果失去了严密性,数学将什么都不是。
20 导数的重建
积分解决了,微分这边也是一样。有了 ε-δ 定义之后,我们就再不能把导数看成是两个无穷小量的比值(dy/dxdy/dxdy/dx),而是:把导数也看成一个极限,对,还是极限。
这个理解起来相对容易,函数在某一点的导数就是这点切线的斜率。我们前面也说了,切线就是当割线的两点不停地靠近,当它们的距离变成无穷小时决定的直线。

很显然,这个定义是依赖无穷小量的,我们现在要用 ε-δ 定义的极限来代替这个无穷小量。所以,切线就应该被理解为割线的极限,那么切线的斜率(也就是这点的导数)自然就是割线斜率的极限,所以导数 f(x)′f(x)'f(x)′也自然而然地成了一个极限。
由于割线的斜率就是用这两点的纵坐标之差 f(x+Δx)−f(x)f(x+Δx)-f(x)f(x+Δx)−f(x) 除以这两点的横坐标之差(x+Δx−x=Δxx+Δx-x=Δxx+Δx−x=Δx),而导数 f(x)′f(x)'f(x)′是割线斜率的极限。那么,我们在割线斜率的前面加一个极限符号就可以表示导数 f(x)′f(x)'f(x)′ 了:
f′(x)=limΔx→0f(x+Δx)−f(x)Δxf'(x)=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}f′(x)=Δx→0limΔxf(x+Δx)−f(x)
这才是导数的真正定义,它是一个极限,而不再是两个无穷小量 dydydy 与 dxdxdx 的商 dy/dxdy/dxdy/dx。也就是说,按照极限的 ε-δ 定义,这个 导数 f(x)′f(x)'f(x)′ 的真正含义是:你任意给一个 ε\varepsilonε,我都能让割线的斜率与这个值的差比你给的 ε\varepsilonε 更小。
我反复强调 ε-δ 定义的含义,就是希望大家能真的从这种角度去理解极限,思考极限,逐渐放弃那种“无限动态趋近某个点”的图景。思维一旦形成定势,想再改过来是非常困难的,所以我们得经常给自己“洗脑”,直到把新理论的核心思想洗到自己的潜意识里去,这样才算真正掌握了它。
我以前讲相对论的时候,很多人在讲相对论时能切换到相对论思维,但是平常一不留神就又跌回到牛顿的思维里去了。然后就闹出了一堆悖论、佯谬和各种奇奇怪怪的东西,这里也一样。
21 微分的重建
莱布尼茨当年认为导数是两个无穷小量 dydydy 和 dxdxdx 的商,所以他用 dy/dxdy/dxdy/dx 来表示导数。虽然现在导数不再是这个意思,但是莱布尼茨当年精心发明的这一套符号确实是非常好用,于是我们就继续沿用了下来。
也就是说,我们今天仍然用**dy/dxdy/dxdy/dx表示导数**,但是大家一定要注意,dy/dxdy/dxdy/dx在现代语境里是一个极限,不再是两个无穷小量的商。
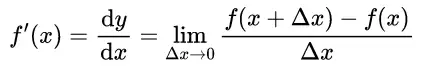
如果不熟悉微积分的历史,就很容易对这些符号产生各种误解,这也是很多科普文、教科书在讲微积分时的一大难点。因为思想是新的,符号却是老的,确实很容易让人犯糊涂。
于是,在莱布尼茨那里,他是先定义了代表无穷小量的微分 dxdxdx 和 dydydy,然后再用微分的商定义了导数 dy/dxdy/dxdy/dx,所以那时候导数也叫微商。

但是现在剧情完全反转了: 我们现在是先用 ε-δ 定义了极限,然后从极限定义导数 dy/dxdy/dxdy/dx。这里压根没有微分什么事,只不过由于历史原因我们依然把导数写成 dy/dxdy/dxdy/dx 这个样子。
那么,dxdxdx和dydydy这两个之前被当作无穷小量的微分的东西,现在还有意义么?
答案是有意义!
这个 dxdxdx和dydydy还是有意义的,当然,有意义也肯定不可能再是以前无穷小量的意思了。那么,在ε-δ 极限这种全新的语境下,dxdxdx 和 dydydy 在新时代的意义又是什么呢?请看下图:

蓝色切线的斜率表示在 PPP 点的导数,如果我们继续用 dy/dxdy/dxdy/dx 表示导数的话,那么从图里就可以清楚的看到:dxdxdx 表示在 xxx 轴的变化量,dydydy 就刚好表示蓝色的切线在 yyy 轴的变化量。
也就是说,当自变量变化了 Δx\Delta xΔx 的时候, Δy\Delta yΔy 表示实际的曲线的变化量,而微分 dydydy则表示这条切线上的变化量,这就是新的语境下 函数微分 dydydy 的含义。而自变量的微分 dxdxdx,大家可以看到,就跟 xxx 轴的变化量 Δx\Delta xΔx 是一回事。由于切线是一条直线,而直线的斜率是一定的。所以,如果我们假设这条切线的 斜率为 AAA,那么 dydydy 和 Δx\Delta xΔx 之间就存在这样一种线性关系:dy=A⋅Δxdy=A·\Delta xdy=A⋅Δx。这些结论都可以很容易从图中看出来,但是,一个函数在某一点是否有微分是有条件的。我们这里是一条很“光滑”的曲线,所以在 PPP 点有微分 dydydy,也就是说它在 PPP 点是可微的。但是,如果函数在 PPP 点是一个折点,一个尖尖的拐点呢?那就不行了。因为有拐点的话,你在这里根本就作不出切线来了,那还谈什么 Δy\Delta yΔy 和 dydydy?关于函数在一点是否可微是一个比较复杂(相对科普的复杂~)的问题,判断曲线(一元函数)和曲面(二元函数)的可微性条件也不太一样。直观地看,如果它们看起来是“光滑”的,那基本上就是可微的。
微分的严格定义是这样的:对于 Δy\Delta yΔy 是否存在着一个关于 Δx\Delta xΔx 为线性的无穷小 A⋅ΔxA·\Delta xA⋅Δx(AAA 为常数),使它与 Δy\Delta yΔy 的差是较 Δx\Delta xΔx 更高阶的无穷小。也就是说,下面这个式子是否成立:
Δy=A⋅Δx+o(Δx)\Delta y=A\cdot\Delta x + o(\Delta x)Δy=A⋅Δx+o(Δx)
o(Δx)o(\Delta x)o(Δx) 就表示 Δx\Delta xΔx 的高阶无穷小,从字面上理解,高阶无穷小就是比无穷小还无穷小。当 Δx\Delta xΔx 慢慢趋向于 0 的时候,o(Δx)o(\Delta x)o(Δx) 能够比 Δx\Delta xΔx 以更快的速度趋向于 0。比如当 Δx\Delta xΔx 减小为原来的 1/10 的时候,o(Δx)o(\Delta x)o(Δx) 就减小到了原来的 1/100,1/1000 甚至更多。
如果这个式子成立,我们就说函数 y=f(x)y=f(x)y=f(x) 在这点是可微的,dy=A⋅Δxdy=A·\Delta xdy=A⋅Δx 就是函数的微分。因为这是一个线性函数,所以我们说 微分 dydydy是 Δy\Delta yΔy 的线性主部。
这部分的内容好像确实有点乏味,莱布尼茨时代的微分 dydydy 就是一个接近 0 又不等于 0 的无穷小量,理解起来非常直观。但是,我们经过 ε-δ 的极限重新定义的函数的微分 dydydy 竟然变成了一个线性主部。这很不直观,定义也挺拗口的,但是这样的微积分才是现代的微积分,才是基础牢固、逻辑严密的微积分。

为了让大家对这个不怎么直观的微分概念也能有一个比较直观的概念,我们再来看一个非常简单的例子。
我们都知道半径为 rrr 的圆的面积公式是 S=πr2S=\pi r^2S=πr2。如果我们让半径增加 Δr\Delta rΔr,那么新的圆的面积就应该写成 π(r+Δr)2\pi(r+\Delta r)^2π(r+Δr)2,那么,增加的面积 ΔS\Delta SΔS 就应该等于两个圆的面积之差:
ΔS=π(r+Δr)2−πr2=2πr⋅Δr+π(Δr)2\Delta S=\pi(r+\Delta r)^2-\pi r^2=2\pi r\cdot\Delta r+\pi(\Delta r)^2ΔS=π(r+Δr)2−πr2=2πr⋅Δr+π(Δr)2
大家看到没有,这个式子就跟我们上面的 Δy=A⋅Δx+o(Δx)\Delta y=A·\Delta x+o(\Delta x)Δy=A⋅Δx+o(Δx)是一模一样的。只不过我们把 xxx 和 yyy 换成了 rrr 和 SSS,AAA 在这里就是 2πr2\pi r2πr,这里的 π(Δr)2\pi(\Delta r)^2π(Δr)2 是关于 Δr\Delta rΔr的平方项,这不就是所谓的高阶(平方是 2 阶,Δr\Delta rΔr 是 1 阶,2 比 1 更高阶)无穷小 o(Δx)o(\Delta x)o(Δx) 么?
所以,它的微分 dsdsds 就是 2πr⋅Δr2\pi r·\Delta r2πr⋅Δr 这一项:
ds=2πr⋅Δrds = 2\pi r\cdot\Delta rds=2πr⋅Δr
它的几何意义也很清楚:这就是一个长为 2πr2\pi r2πr(这刚好是圆的周长),宽为 Δr\Delta rΔr 的矩形的面积,好像是把这个圆“拉直”了所得的矩形的面积。
好了,微分的事情就说到这里,剩下的大家可以自己慢慢去体会。毕竟这是一篇关于微积分的科普文,再写太多就成教材了。
22 收官的勒贝格
关于微积分的重建,我们已经看到了如何在 ε-δ 定义的新极限下重新定义了积分和微分,也看到了在这种新的定义下,积分和微分的概念跟以前有什么不同。沿着这条路,我们还能非常严格的证明微积分基本定理,也能很好地处理连续性、可微性、可导性、可积性等问题。虽然在具体的计算方式上跟以前的差别不大,但是微积分的这个逻辑基础已经跟以前发生了翻天覆地的变化,这个差别大家要仔细体会。
在魏尔斯特拉斯给出极限的 ε-δ 定义之后,微积分的逻辑问题基本上解决了,但还有一些其它的问题。比如,有了微积分,数学家们当然就希望尽可能多的函数是可以求出积分的,但是你像来砸场子的狄利克雷函数(xxx 为有理数的时候值为 1,xxx 为无理数的时候值为 0)就没法这样求积分。
不信你想想,一个在有理数为 1,无理数为 0 的函数你要怎么去切块?它在任何一个地方都是不连续的,你甚至连它的图像都画不出来,怎么用矩形去逼近?所以,这里就有一个棘手的问题:一个函数到底要满足什么条件才是可以求积分的呢?
这个问题一直拖到 20 世纪初才由大神勒贝格解决。勒贝格把我们常见的长度、面积概念做了一个扩展,得到了更一般的测度的概念。然后,他基于这种测度定义了适用范围更广的勒贝格积分,于是,原来无法求积分的狄利克雷函数在勒贝格积分下就可以求积分了。然后,勒贝格基于测度的理论也给出了一个函数是否可积的判断条件,完美收官!

于是,我们这段跨越两千多年,从阿基米德到勒贝格的微积分之旅就要告一段落了。
23 结语
古希腊人和古代中国人都知道用已知的多边形去逼近复杂曲线图形,阿基米德用穷竭法算出了一些简单曲线围成的面积,刘微用正多边形去逼近圆,也就是用割圆术去计算圆周率。
牛顿和莱布尼茨发现了“微分和积分是一对互逆运算”这个惊天大秘密,正式宣告了微积分的诞生。
柯西和魏尔斯特拉斯用 ε-δ 语言重新定义了极限,把风雨飘摇中的微积分重新建立在坚实的极限理论基础之上,彻底解决了幽灵般的无穷小量的问题,解决了第二次数学危机,也在数学领域解决了芝诺悖论。
勒贝格基于集合论,对积分理论进行了一次革命,建立了定义范围更广的勒贝格积分,并且进一步把这场革命推进到了实分析。
我的文章虽然以勒贝格结尾,但这丝毫不代表微积分在勒贝格这里就走向了完结,即便这时候已经是 20 世纪初了。
∫abf(x)dx=F(b)−F(a)\int\limits_{a}^{b}{f\left( x \right)}\text{d}x=F\left( b \right)-F\left( a \right)a∫bf(x)dx=F(b)−F(a)
20 世纪 60 年代初,有一个叫鲁滨逊的德国人重新捡起了莱布尼茨的无穷小量。他把实数扩展到非实数,直接把无穷大和无穷小变成了非实数域里的一个元素。所以他的理论可以直接处理无穷小量,这是第一个严格的无穷小理论。
我们知道,幽灵般的无穷小量在微积分建立初期掀起了腥风血雨,后来经过柯西和魏尔斯特拉斯的拼命抢救,才终于在坚实的 ε-δ 极限理论 之上重建了微积分。柯西和魏尔斯特拉斯的这一套让微积分严密化的方法被称为标准分析。
而鲁滨逊认为,无穷小量虽然不严谨,但是大家基于无穷小量做的微积分计算却也都是正确的,这至少表明无穷小量里应该也包含着某种正确性。ε-δ 极限是一种绕弯解决无穷小量不严谨的方法,但是这种方法并不是唯一的。鲁滨逊选择直接面对无穷小量,直接建立了另一种让微积分严密化的方法。因此,与柯西和魏尔斯特拉斯的标准分析相对,鲁滨逊的这种方法被称为非标准分析。

提出了不完备定理的数学大神哥德尔就对非标准分析推崇备至,他认为非标准分析将会是未来的数学分析。他说:“在未来的世纪中,将要思量数学史中的一件大事,就是为什么在发明微积分 300 年后,第一个严格的无限小理论才发展起来。”
我们现在就处在哥德尔说的未来的世纪中,各位看官对这个问题有没有什么看法呢?如果我的这篇文章能够让大家对微积分,对数学感兴趣,进而开始自己独立的思考这些问题,那就善莫大焉了~
此外,数学不等于计算,数学也不等于应用,绝妙而深刻的数学思想(比如发现微分和积分是互逆过程)和严密的逻辑(如使用 ε-δ 定义极限)反而是更重要的。而且,数学的壮观之美也往往需要站在后面两个角度上才能体会到,我很难相信有人会觉得重复的做计算是很有趣的,这也是很多人不喜欢数学的原因。但是,我绝对相信那些真正认识了数学的人,他们是发自内心的觉得数学美丽动人。
并非数学家们怪异,而是他们确实看到了常人未曾察觉的绝美风景。
微积分学习资源推荐
原创 长尾君 长尾科技 2019年12月06日 17:41
1. 微积分历史
- 《微积分的历程:从牛顿到勒贝格》(William Dunham)
- 详细介绍了微积分发展过程中主要人物的贡献,涵盖伯努利兄弟、欧拉、黎曼等人的工作,既有通俗介绍,又有严谨的公式推导,适合对微积分历史感兴趣的学生。
- src(tqm:jebt)
- 《古今数学思想》(莫里斯·克莱因)
- 全面讲述数学发展史,涵盖微积分及其他数学领域的历史脉络,适合对数学史有浓厚兴趣的学生。
- src(tqm:jwa4)
2. 入门友好型教材
- 《普林斯顿微积分读本》(Adrian Banner)
- 适合初学者自学,讲解清晰,注重学习过程中的常见问题与易错点,文字丰富,公式推导详细,适合初学者逐步建立微积分知识体系。
- src(tqm:8hin)
- 《托马斯微积分》(George B. Thomas)
- 经典的美式教材,适合自学,内容详实,注重物理背景与几何直观,有助于初学者理解微积分的基本概念与应用。
- src(tqm:jgw7)
3. 通俗微积分科普
- 《简单微积分》(神永正博)
- 极通俗的微积分科普书籍,适合中小学生及零基础读者入门。
- (src暂未找到)
- 《什么是数学》(柯朗与罗宾)
- 从自然数讲起,逐步深入至微积分,重点在于数学思想方法的研究,适合所有对数学感兴趣的学生。
- src(tqm:d6tm)
4. 严密型教材
- 《微积分学教程》(菲赫金哥尔茨)
- 从自然数出发,逐步严密推导微积分体系,兼具严密性与通俗性。书中包含大量物理与几何实例,适合对微积分严密性有较高要求的学生。
- src(tqm:73f1)
5. 进一步学习升级-实分析
- 《陶哲轩实分析》(陶哲轩)
- 从自然数的皮亚诺公理出发,逐步推导实分析的基本内容,注重数学严密性,适合对数学严密性有较高要求的学生。
- src(tqm:jwa4)
- 《线性代数应该这样学》(Axler)
- 内容详实,讲解清晰,适合学习线性代数的学生。
- 暂未找到
微积分到底是什么?— 上文概览版
原创 长尾君 长尾科技_ 发布于 2019-12-01 17:46・湖北
01 从面积说起
1.1 穷竭法:阿基米德求抛物线弓形面积
- 图形:抛物线 y=kx2y = k x^2y=kx2 与直线 BCBCBC 围成弓形。
- 步骤
a. 取抛物线顶点 AAA,作三角形 △ABC\triangle ABC△ABC,使得 AB,ACAB,\ ACAB, AC 为抛物线切线且 BCBCBC 平行于 AAA 点切线。
b. 面积关系:
弓形面积=43△ABC.\text {弓形面积} = \frac {4}{3} \triangle ABC.弓形面积=34△ABC.
c. 证明思路:- 第一次逼近:用 △ABC\triangle ABC△ABC,剩余两个小弓形。
- 第二次逼近:在每个小弓形内再作三角形,面积缩小为上一轮 1/41/41/4。
- 形成几何级数:
总面积=△ABC(1+14+142+…)=△ABC11−1/4=43△ABC.\text {总面积} = \triangle ABC \left ( 1 + \frac {1}{4} + \frac {1}{4^2} + \dots \right) = \triangle ABC \frac {1}{1 - 1/4} = \frac {4}{3} \triangle ABC.总面积=△ABC(1+41+421+…)=△ABC1−1/41=34△ABC.
1.2 矩形逼近:求 y=x2y = x^2y=x2 在 [0,1][0,1][0,1] 的面积
- 将 [0,1][0,1][0,1] 均分为 nnn 份,每份宽 Δx=1/n\Delta x = 1/nΔx=1/n。
- 第 kkk 个矩形高 (kn)2\left ( \frac {k}{n} \right)^2(nk)2,面积
Sn=∑k=1n1n(kn)2=1n3∑k=1nk2.S_n = \sum_{k=1}^{n} \frac {1}{n} \left ( \frac {k}{n} \right)^2 = \frac {1}{n^3} \sum_{k=1}^{n} k^2.Sn=k=1∑nn1(nk)2=n31k=1∑nk2. - 代入平方和公式
∑k=1nk2=n(n+1)(2n+1)6,\sum_{k=1}^{n} k^2 = \frac {n (n+1)(2n+1)}{6},k=1∑nk2=6n(n+1)(2n+1),
得
Sn=(n+1)(2n+1)6n2=13+12n+16n2.S_n = \frac {(n+1)(2n+1)}{6n^2} = \frac {1}{3} + \frac {1}{2n} + \frac {1}{6n^2}.Sn=6n2(n+1)(2n+1)=31+2n1+6n21. - 极限
limn→∞Sn=13.\lim_{n\to\infty} S_n = \frac {1}{3}.n→∞limSn=31.
02 一千年以后:17 世纪的统一矩形法
- 任意曲线 y=f(x)y = f (x)y=f(x),区间 [a,b][a,b][a,b] 分成 nnn 份:
面积≈∑i=1nf(xi)Δxi.\text {面积} \approx \sum_{i=1}^{n} f (x_i)\Delta x_i.面积≈i=1∑nf(xi)Δxi. - 令最大宽 maxΔxi→0\max \Delta x_i \to 0maxΔxi→0,定义
∫abf(x)dx=limmaxΔxi→0∑i=1nf(xi)Δxi.\int_a^b f (x)\,dx = \lim_{\max \Delta x_i \to 0} \sum_{i=1}^{n} f (x_i)\Delta x_i.∫abf(x)dx=maxΔxi→0limi=1∑nf(xi)Δxi.
03 严密性与实用性
| 方法 | 操作 | 逻辑 | 局限 |
|---|---|---|---|
| 穷竭法 | 图形特化逼近 | 严谨 | 技巧复杂 |
| 17 世纪矩形法 | 统一分割 | 直觉 | 无穷小量不严谨 |
04 初见积分:符号与含义
∫abf(x)dx\int_a^b f (x)\,dx∫abf(x)dx
表示曲线 y=f(x)y = f (x)y=f(x) 与 xxx 轴在 [a,b][a,b][a,b] 围成的带符号面积。
05 直线与斜率
- 直线通过两点 (x0,y0),(x1,y1)(x_0,y_0),\ (x_1,y_1)(x0,y0), (x1,y1):
k=y1−y0x1−x0.k = \frac {y_1 - y_0}{x_1 - x_0}.k=x1−x0y1−y0. - 与 xxx 轴夹角 θ\thetaθ:
k=tanθ.k = \tan\theta.k=tanθ.
06 曲线与切线
- 割线 ABABAB 斜率
f(x+Δx)−f(x)Δx.\frac {f (x+\Delta x)-f (x)}{\Delta x}.Δxf(x+Δx)−f(x). - 当 Δx→0\Delta x \to 0Δx→0,割线极限位置为切线,其斜率定义为
f′(x)=limΔx→0f(x+Δx)−f(x)Δx.f'(x) = \lim_{\Delta x \to 0} \frac {f (x+\Delta x)-f (x)}{\Delta x}.f′(x)=Δx→0limΔxf(x+Δx)−f(x).
07 初见微分:莱布尼茨记法
- 引入无穷小 dx,dydx,\ dydx, dy:
dydx=f′(x).\frac {dy}{dx} = f'(x).dxdy=f′(x). - 注意:此时 dx≠0dx \ne 0dx=0,但可 “无限接近 0”。
08 导数:定义与计算
例 1:f(x)=x2f (x) = x^2f(x)=x2
f′(x)=limh→0(x+h)2−x2h=limh→02xh+h2h=limh→0(2x+h)=2x.\begin {aligned} f'(x) &= \lim_{h\to 0}\frac {(x+h)^2 - x^2}{h} \\ &= \lim_{h\to 0}\frac {2xh + h^2}{h} \\ &= \lim_{h\to 0}(2x + h) = 2x. \end {aligned} f′(x)=h→0limh(x+h)2−x2=h→0limh2xh+h2=h→0lim(2x+h)=2x.
09 导数的意义
| 场景 | 导数含义 |
|---|---|
| 位移 s(t)s (t)s(t) | 瞬时速度 v(t)=s′(t)v (t) = s'(t)v(t)=s′(t) |
| 利润函数 P(x)P (x)P(x) | 边际利润 P′(x)P'(x)P′(x) |
| 曲线 y=f(x)y = f (x)y=f(x) | 切线斜率 f′(x)f'(x)f′(x) |
极值必要条件:f′(x0)=0f'(x_0) = 0f′(x0)=0。
10 互逆运算:积分与微分的发现
- 牛顿 - 莱布尼茨洞察:
若 F′(x)=f(x)F'(x) = f (x)F′(x)=f(x),则
∫abf(x)dx=F(b)−F(a).\int_a^b f (x)\,dx = F (b) - F (a).∫abf(x)dx=F(b)−F(a).
即积分与微分互为逆运算。
11 v-t 图像与位移
- 匀速:矩形面积 vΔtv\Delta tvΔt。
- 变速:
位移=∫t1t2v(t)dt.\text {位移} = \int_{t_1}^{t_2} v (t)\,dt.位移=∫t1t2v(t)dt. - 逆运算:
v(t)=ddt(∫t0tv(τ)dτ).v (t) = \frac {d}{dt}\left (\int_{t_0}^t v (\tau)\,d\tau\right).v(t)=dtd(∫t0tv(τ)dτ).
12 原函数(不定积分)
定义:若 F′(x)=f(x)F'(x) = f (x)F′(x)=f(x),则
∫f(x)dx=F(x)+C.\int f (x)\,dx = F (x) + C.∫f(x)dx=F(x)+C.
13 微积分基本定理(牛顿 - 莱布尼茨公式)
定理:设 fff 在 [a,b][a,b][a,b] 连续,FFF 为其任一原函数,则
∫abf(x)dx=F(b)−F(a).\int_a^b f (x)\,dx = F (b) - F (a).∫abf(x)dx=F(b)−F(a).
例 2:用基本定理重算 ∫01x2dx\int_0^1 x^2\,dx∫01x2dx
- 原函数 F(x)=x33F (x) = \frac {x^3}{3}F(x)=3x3。
- 计算
F(1)−F(0)=13−0=13.F (1) - F (0) = \frac {1}{3} - 0 = \frac {1}{3}.F(1)−F(0)=31−0=31.
14 数学的力量:通用化与机械化
-
鸡兔同笼问题 → 方程组
{x+y=35,2x+4y=94.\begin {cases} x + y = 35, \\ 2x + 4y = 94. \end {cases}{x+y=35,2x+4y=94.
程序化求解,替代特化技巧。 -
微积分同理:将面积、长度、体积统一为求原函数。
15 进击的微积分:扩展方向
| 领域 | 工具 |
|---|---|
| 复合函数积分 | 换元、分部积分 |
| 多元积分 | 重积分、曲线 / 曲面积分 |
| 微分几何 | 切空间、曲率 |
| 物理方程 | 微分方程、变分法 |
16 被忽略的无穷小:逻辑危机
- 无穷小量 dxdxdx 既 “非零” 又 “可舍”,矛盾。
- 第二次数学危机。
17 柯西极限思想
定义(柯西,1821):
变量 xnx_nxn 极限为 LLL 当且仅当
对任意 ε>0\varepsilon > 0ε>0,存在 NNN,使 n>Nn > Nn>N 时 ∣xn−L∣<ε|x_n - L| < \varepsilon∣xn−L∣<ε。
18 魏尔斯特拉斯 ε\varepsilonε-δ\deltaδ 极限
定义(魏尔斯特拉斯,1861):
函数 fff 在 aaa 处极限为 LLL,记
limx→af(x)=L\lim_{x \to a} f (x) = Lx→alimf(x)=L
当且仅当
∀ε>0,∃δ>0,0<∣x−a∣<δ⇒∣f(x)−L∣<ε.\forall \varepsilon>0,\ \exists \delta>0,\ 0<|x-a|<\delta \Rightarrow |f (x)-L|<\varepsilon.∀ε>0, ∃δ>0, 0<∣x−a∣<δ⇒∣f(x)−L∣<ε.
例 3:limx→∞1x=0\lim_{x \to \infty} \frac {1}{x} = 0limx→∞x1=0
- 给定 ε>0\varepsilon>0ε>0,取 δ=1/ε\delta = 1/\varepsilonδ=1/ε,则 x>δx > \deltax>δ 时
∣1x−0∣<ε.\left|\frac {1}{x} - 0\right| < \varepsilon.x1−0<ε.
19 积分的重建:黎曼积分
- 分割 [a,b][a,b][a,b]:a=x0<x1<⋯<xn=ba = x_0 < x_1 < \dots < x_n = ba=x0<x1<⋯<xn=b。
- 黎曼和
Sn=∑i=1nf(ξi)Δxi,ξi∈[xi−1,xi].S_n = \sum_{i=1}^{n} f (\xi_i)\Delta x_i,\quad \xi_i \in [x_{i-1},x_i].Sn=i=1∑nf(ξi)Δxi,ξi∈[xi−1,xi]. - 若极限
limmaxΔxi→0Sn\lim_{\max \Delta x_i \to 0} S_nmaxΔxi→0limSn
存在,则称 fff 黎曼可积,记
∫abf(x)dx=limmaxΔxi→0Sn.\int_a^b f (x)\,dx = \lim_{\max \Delta x_i \to 0} S_n.∫abf(x)dx=maxΔxi→0limSn.
20 导数的重建
定义:
f′(a)=limx→af(x)−f(a)x−a=limh→0f(a+h)−f(a)h.f'(a) = \lim_{x \to a} \frac {f (x)-f (a)}{x-a} = \lim_{h \to 0} \frac {f (a+h)-f (a)}{h}.f′(a)=x→alimx−af(x)−f(a)=h→0limhf(a+h)−f(a).
21 微分的重建:现代意义
- 设 fff 在 xxx 可导,则
Δy=f(x+Δx)−f(x)=f′(x)Δx+o(Δx).\Delta y = f (x+\Delta x)-f (x) = f'(x)\Delta x + o (\Delta x).Δy=f(x+Δx)−f(x)=f′(x)Δx+o(Δx). - 定义
dy=f′(x)dx,dx=Δx.dy = f'(x)\,dx,\quad dx = \Delta x.dy=f′(x)dx,dx=Δx. - 几何:dydydy 为切线纵向增量。
例 4:圆面积微分
S=πr2S = \pi r^2S=πr2,取 dSdSdS:
ΔS=π(r+Δr)2−πr2=2πrΔr+π(Δr)2,\Delta S = \pi (r+\Delta r)^2 - \pi r^2 = 2\pi r\Delta r + \pi (\Delta r)^2,ΔS=π(r+Δr)2−πr2=2πrΔr+π(Δr)2,
故
dS=2πrdr.dS = 2\pi r\,dr.dS=2πrdr.
22 勒贝格积分:20 世纪收官
-
狄利克雷函数
D(x)={1,x∈Q,0,x∉Q,D (x) = \begin {cases} 1, & x \in \mathbb Q, \\ 0, & x \notin \mathbb Q, \end {cases}D(x)={1,0,x∈Q,x∈/Q,
黎曼不可积,但勒贝格可积,且
∫01D(x)dμ=0.\int_0^1 D (x)\,d\mu = 0.∫01D(x)dμ=0. -
勒贝格测度与积分:扩大可积函数类,奠定实分析基础。
23 结语:两千年的微积分旅程
| 阶段 | 人物 | 贡献 |
|---|---|---|
| 古代 | 阿基米德 | 穷竭法 |
| 17 世纪 | 牛顿 - 莱布尼茨 | 互逆运算,微积分诞生 |
| 19 世纪 | 柯西 - 魏尔斯特拉斯 | ε\varepsilonε-δ\deltaδ 极限,严密化 |
| 20 世纪初 | 勒贝格 | 测度积分 |
| 20 世纪中 | 鲁滨逊 | 非标准分析,复活无穷小 |
从面积、斜率的朴素问题出发,到极限、测度的严谨体系,微积分完成了两千年的进化,并成为现代科学与数学的共同语言。
微积分体系几百年前就建立起来了,为什么我们现在学习它仍存在困难?
Yuhang Liu(5186 人赞同了该回答)
学习动机的差异:被动接受与主动探索
因为你是被动的接受这些知识,你可能对求椭圆面积或者变力做功并不感兴趣,你更关心他们有哪些实际的看得见摸得着的应用。你缺乏学习的动机。
但是牛顿、莱布尼兹创立微积分的时候,他们是真的想解决那个时代没有解决的问题。他们有强烈的动机。生产实践中处理不规则图形面积或者其他需要用到积分原理的场合比比皆是,但是数学仍然处在“常量时代”,处理不了这些基本的微积分问题,这简直是那个时代数学的“耻辱”。同时那个时代极限的观念已经趋于成熟,即使没有牛顿、莱布尼兹、欧拉等等,也会有其他的人建立一套方法论,告诉我们怎么去求 exe^xex 函数图像下包围的面积,告诉我们怎么去推导最速降线方程,告诉我们怎么去建立流体力学方程来研究流体的性质。因为这是人类文明发展进步的必经之路。
时代问题与认知格局的差距
我们这个时代同样有很多伟大的科学问题。纯数学里面种种猜想,宇宙学中暗物质暗能量的探索,相对论与量子场论统一的尝试;工业上流体的湍流现象仍然没有很好的数学描述,深度学习的可解释性远未解决。等等等等。只不过大部分人不关心这些,他们理所当然地生活在现在的科技水平之下,正如同工业革命以前的人理所当然地生活在田园牧歌时代一样。他们看不到头顶的星空,对未来没有憧憬和想象。
任何时代都是一小撮科学伟人凭借着自己的探索欲不断突破那个时代科学认知的天花板。这个时代的普通人相比牛顿时代的普通人而言,知识量当然更大,但是思想格局很难说有重大改变。这个时代的大学生学习高数的时候,只是感觉到“好难”、“学不会”;他们体会不到科学先贤们对未知领域的强烈探索欲、征服欲,这些欲望驱使他们花费几年、几十年甚至一生的时间去建立、完善一个理论。普通人和伟人的差距真的不仅仅在智商,更在于思想境界,在于动机。
编辑于 2020-12-19 22:18
Hsin(1325 人赞同了该回答)
科学求真
微积分的历史演变:从直观到严谨
因为我们现在看到的教科书,已经远远偏离了微积分最初的样子。
微积分不是在几百年前“刷”地一下就完备地出现在所有人面前,而是在出现后的几百年里修修补补,才变成了今天的这套体系。从历史上看,它是一个实践先于理论的过程。早期的微积分其实很简单,采用一种实用主义的态度,能算出来就行,而对底层逻辑的要求非常宽松,“微积分的先驱们多半依靠直觉而不是根据推理进行计算”[1]。比如说,在牛顿和莱布尼兹创建微积分的时候,使用的证明方法都还是几何直觉与代数技巧相混杂的大杂烩,而且都埋伏着致命的逻辑漏洞。
早期微积分的逻辑漏洞:无穷小的困境
最致命的一点就是「无穷小」的概念:一个既等于零、又不等于零的幽灵。在牛顿的“流数术”中,当需要除以一个无穷小量 ooo 的时候,它被看作了一个非零量,而在需要舍去一个多项式后面含 ooo 的分量的时候,它们又会被当作0而消去。莱布尼兹也有同样的问题,一个极小的长度 dxdxdx ,被看作了一个无限小的不可能再分的长度。但这样说显然只是一个逻辑上的权宜之计,很多人并不买账,多小是不可再分?一定有一个不可再分的量吗?
关于……无限小,我们理解为……某种无限的小,所以每次分割本身都成为一个级别,只不过不是一个最后的级别。如果有谁希望将这些[无限小]理解为最终的事物……,那么,这也是可以的,而且也不会陷入关于延伸范围或者一般而论的无限连续统或者无限小的真实性的争论中,即使他认为这样的事是完全不可能的。
——莱布尼兹
在历史上这样的逻辑漏洞甚至牵扯到了宗教信仰,并招来猛烈的批评(天主教学校是有数学这门课的,主教们都是数学上的一把好手)[2]。
这些流数到底是什么?逐渐消失的增量的速度有多么大?这些相同的逐渐消失的增量是什么?他们既不是有限的量,也不是无穷小的量,更不是零。难道我们不能把它们称为消逝的量的鬼魂吗?
错误也许能产生真理,但是决不会产生科学。
——伯克莱主教
这样的质疑其实是有道理的,虽然实践已经证明了早期的微积分确实是求切线和确定极大值或极小值的极好工具,但是能得到正确的结果,并不能掩盖理论本身仍然存在无法回避的漏洞,万一是负负得正,凑巧蒙对的呢?“如果一个正确的答案来自于错误的思想,反而会掩盖其中隐藏的漏洞,就像在某种错误补偿中某些错误抵消其它错误”(惊,18世纪的控制论思想)。
柯西的贡献:以极限为基础的严密化
正是为了填补早期微积分基础不牢的漏洞,这个体系开始逐渐脱离直觉世界而转向晦涩。很多人在其中做出了贡献,达朗贝尔和拉格朗日都尝试过在新的概念基础上构建微积分的理论体系,但最后都没有成功。最后,在19世纪初期,是柯西最终完成了微积分体系的严密构建,使之成为了一个充满抽象性和不等式的学科。
柯西的办法是把全部微积分建立在极限思想的基础上:
当属于一个变量的相继的值无限地趋近于某个固定值时,如果最终同固定值之差可以随意地小,那么这个固定值就称为所有这些值的极限。
翻译一下,这便是现代微积分中我们熟悉的 ϵ−δ\epsilon-\deltaϵ−δ 语言。明确了极限的定义,下一步是导出连续性的概念,进而重构整个微分和积分。从这部分开始,就进入了教科书的范围。
通过上面的极限定义,整个微积分的构造才完全规避了对「无穷小」这个含糊不清概念的依赖。定义不提及怎样到达极限,仅仅是接近并保持接近它,因此这里也就不存在所谓消逝又没有消逝的无穷小量鬼魂。即使在一些教材中再提到无穷小这个名词,也只是起到一些简化讨论的作用,并不会让整个体系伤筋动骨。
形而上一些地讲,早期的微积分将无穷小看作是一个静止的常量,却用动态的手段去使用它,因而留下了致命的逻辑漏洞;而柯西重建的微积分直接用一个动态的定义作为所有概念的思想基础,从而给出了一个严密的微积分理论体系。当然,逻辑上趋于严密的代价便是形式上变得晦涩抽象。 对于初学者来说,完全摒弃直觉,也并不符合人的认知规律。所以回到问题本身,就显得好像过了几百年,微积分反而越学越难。
以上大部分内容整理自下面这本书,感兴趣可以进一步阅读。不吹不黑,这本书对微积分历史上遇到的各种问题和解决思路都介绍得非常清晰,非常值得一看。
还有一本讲无穷小的书,更偏向于从历史科普的角度出发,比如主教们为什么也要学数学、意大利以伽利略为首的数学家们受到的宗教压制等等,而对具体的数学原理涉及不深,也有一定的参考价值。
参考
- 1.微积分的历程 (豆瓣)
https://book.douban.com/subject/4904723/ - 2.无穷小 (豆瓣)
https://book.douban.com/subject/33446874/
万军取首高数线代(419 人赞同了该回答)
教材的缺陷:抽象语言与认知脱节
先说结论:因为我们的教材,尤其是《同济版高数》,并没有给出引入微积分的目的,而是一上来就用一大堆抽象繁杂的数学语言,让我们从第一节课就学不会。就比如说 ϵ−δ\epsilon-\deltaϵ−δ 语言,对于一个刚参加完高考的大学生来说,太复杂了。由于它包含了多个“任意”“存在”等词汇,他们甚至没法轻易写出这个命题的否命题、逆命题和逆否命题,自然做题会懵逼。
大家学了这么久的微积分,想必很清楚微积分离不开极限的概念——极限、连续、导数都是什么呢?首先是极限,它的 ϵ−δ\epsilon-\deltaϵ−δ 语言(以及 ϵ−N\epsilon-Nϵ−N 语言)确实足以让许多同学无法理解。但是在我眼里,它是没那么不自然的——这是因为,它已经可以来自很多你不太陌生的极限过程了。

比如这个等比求和数列,在直观(矩形的面积之和)上, SnS_nSn 在接近于 a11−q\frac{a_1}{1-q}1−qa1 ,写成数学语言就是 limn→∞Sn=a11−q\lim_{n \to \infty} S_n=\frac{a_1}{1-q}limn→∞Sn=1−qa1 。
或者是一些圆锥曲线大题,像 S=1+k22+k2S=\frac{1+k^2}{2+k^2}S=2+k21+k2 这种表达式估计已经写到你想吐了。如果直线的斜率 kkk 不存在(相当于斜率是无穷大),你甚至不需要单独算一个结果,只需要观察表达式就可以知道这种条件下 S=1S=1S=1 。写成数学语言就是, limk→∞1+k22+k2=1\lim_{k \to \infty}\frac{1+k^2}{2+k^2}=1limk→∞2+k21+k2=1 。
几何直观与数学语言的联系
在没有 ϵ−δ\epsilon-\deltaϵ−δ 语言的条件下,我们还是通过直觉,产生了极限的概念,而这种语言,只不过是把这个过程严谨化了而已。这,就是几何直观与数学语言之间的联系。一旦学生明白了为什么要这样定义之后,很多题目,我们甚至可以抛弃定义,直接画个图像就能把错误选项排除掉。
比如,极限为什么唯一呢?还是上面那个例子,你肯定不会说极限是 1.00000000001,即使它和 1 很接近。一旦极限不唯一,那么“无限趋近”的定义不就乱套了吗?所以必然唯一。
连续与导数的直观理解
然后说说连续。有了极限的感觉,你可以想一想,如果一个函数满足 limx→x0f(x)=f(x0)\lim_{x \to x_0}f(x)=f(x_0)limx→x0f(x)=f(x0) ,会发生什么呢?

既然有这样一个无限接近的感觉,那么在 x=x0x=x_0x=x0 附近,函数值都被限制在 f(x0)f(x_0)f(x0) 附近了,也就是说不会有一种突变,而会有一种连续变化的感觉,比如上面的那个函数就是这样。而这就是函数的连续性。
反过来,不连续的函数,在图像上就会让你感受到它的间断性。

最后是导数,它代表切线的斜率。什么是切线呢?我们先看一个实例:汽车行驶的位移与导数。
我们先回忆下平均速度的定义。我们知道,如果汽车的位移是 x(t)x(t)x(t) ,汽车在 [t1,t2][t_1,t_2][t1,t2] 内的平均速度,就是 x(t2)−x(t1)t2−t1\frac{x(t_2)-x(t_1)}{t_2-t_1}t2−t1x(t2)−x(t1) 。从几何上来看,它代表的是 x−tx-tx−t 图像上割线的斜率。

平均速度的计算十分简单,只需要汽车的初态和末态便可得到。然而,这种便捷性也是它的一个问题——平均速度只能反映初态和末态,无法反映汽车在 [t1,t2][t_1,t_2][t1,t2] 每一时刻的状态!
这个“每一时刻的状态”,就是瞬时速度。如果我们把求平均速度的区间逐渐缩小,直到缩小为十分接近于一个点时,这个速度就越接近我们想要的那个瞬时速度。在极限情况下,这就是瞬时速度!
也就是说,导数代表汽车行驶的瞬时速度!从几何上来看,它代表的是 x−tx-tx−t 图像上切线的斜率。由于切线就是割线的极限情况,因此代数上的极限和几何上的极限,在这里是一致的。
微积分概念的认知基础
从这里来看,极限、连续、导数的概念对于一个新大学生来说,似乎并不陌生。极限的概念可以来自于圆锥曲线中,直线斜率趋近无穷大时各个量的变化,也可以来自于无穷递缩等比数列;连续的概念,其实他们在学零点存在性定理的时候就有了,只是没有用严谨的数学语言表示出来;而导数就是物理课上学过的瞬时速度。
真实的微积分,也是这样建立起来的——正是因为我们需要描述瞬时速度,我们才有了极限和导数的概念。而我们的课堂如果除了数学语言啥也不讲的话,学生上课不睡觉才怪呢!
发布于 2024-10-10 09:38
流浪在远方的忧伤(138 人赞同了该回答)
大学与中学数学的差异及学习困境
个人认为,产生这种现象的原因,主要是在于:
- 进入大学后,没有认识到大学数学和中学数学的差异,大学数学研究的对象更抽象(比如线性方程组的解集,函数和集合,群环域),更关注于研究抽象结构的属性,更强调逻辑以及逻辑的严谨,而非计算(当然微积分也有很多计算,但相对来说,微积分的证明更能体现大学数学的特点),学习方式,没有转变过来。
- 我们的教材,缺乏系统性的设计,内容框架和排布欠缺合理性,很多学校,都使用本校老师编写的教材,很多本校教材的质量,其实可能不高。
- 老师在授课时,没有讲清楚其背后的逻辑思想,讲授方式过于生硬,念ppt多,板书少。
针对微积分的基本思想,我写了一个几万字的微积分漫谈,通过介绍微积分形成过程,解释微积分的主要思想,但是,它并不是一个数学史,而是重点在于介绍其背后的数学思维,以及逻辑演变过程和基础,相信它可以作为大学微积分教材的有益补充。
关键是,个人认为写的,还算比较幽默,有趣儿。
读了我写的微积分漫谈系列,可以解答上学时的一些困惑,例如:
- 微积分是如何产生的,是为了解决什么问题而产生的?为什么教科书上的微积分,变成了这么晦涩难懂的东西?
- 微积分的核心思想和本质是什么?它的很多思想,背后的逻辑是什么?
- 为什么工科高等数学教材,第一章通常要去讲数列的极限,而数学分析教材,第一章通常要去讲实数?
在本回答的最后,可以看到各个章节的链接。
大学数学的特点
下面是我关于大学数学和中学数学的学习差异,做出的一些简要介绍:
大学学习的数学,和中学的数学,差异,还是稍微有那么一点儿点儿多的。
大学数学的一个特点是,更抽象,而且很多学科,都聚焦在研究相关抽象结构,探索其性质和隐含的规律。
说大学数学抽象,主要是研究集合和映射,整数/有理数/实数/复数各种数系,群,环,域…都是集合,线性变换,矩阵…都是映射,函数还是从集合到集合的映射。
而且大学数学,不拼计算,比如线性代数,严格来说,只有加法和乘法,根本不是让你去计算去解方程组,但是对于解集所形成的线性空间及其属性,却是连篇累牍。微积分,更是聚焦函数的性质,进行深入分析。
所以,大学数学,不但研究抽象的东西,还要探索其普遍规律,这就有点离谱了。
中学的数学,无论是平面几何,立体几何,还是初等函数,相对而言,更具体一些。而大学数学,你会看到,各种奇奇怪怪的曲线/图形和体积,像“托里拆利小号”都是属于长得眉清目秀的。
所以,你得适应从颜控看脸的,变成习惯抽象派,甚至野兽派(比如处处连续处处不可导的Weierstrass函数)。
另外,大学数学的符号,也非常多,尤其是逻辑符号( ∀,∃,⇒,ϵ−δ,⋯\forall,\exists,\Rightarrow,\epsilon-\delta,\cdots∀,∃,⇒,ϵ−δ,⋯ )和各种抽象符号。其实,天天看,也就熟悉了,表担心。
大学数学的第二个特点,比中学数学,更讲究逻辑,而很多结论,通常是"反常识",但绝不会反逻辑。
当高中老师在课堂上介绍 0.9˙=10.\dot{9}=10.9˙=1 时,当初习惯了初等数学思维的我们,简直觉得天都塌了: 0.9˙0.\dot{9}0.9˙ 啊,小数点儿后面都是9啊,不是比1还差一点儿吗?怎么可能会相等?喔, 0.3˙=130.\dot{3}=\frac{1}{3}0.3˙=31 ,还好还好,还在正常思维之内。
但是,大学数学,都会涉及到无穷,只要一进入无穷,很多看起来奇奇怪怪的东西,都会跑出来,产生让人崩溃的结论:
- 比如希尔伯特旅馆问题,一个集合的真子集,居然和全集能形成一一对应?
- 都是无穷多,整数的无穷是可数的,有理数比整数多多了,居然还是可数的,而实数居然是不可数的?
- …
大学数学的第三个特点,是讲究逻辑的严谨,公理化演绎一切的倾向极其明显,中学数学,更多的是,定理的应用和各种应用技巧,还是“术”,而大学数学,更接近“道”。
你会看到很多“似乎不证自明”的问题,在那里推导,或者要你去证明,这也要证?
你还会看到,有人费劲巴力地定义一个你已经自认为很熟悉的东西,比如居然用一个有理数数列,去定义一个实数,还有用戴德金分割去定义实数的。
我们在中学经常使用的数学归纳法,为什么能用呢?因为,它其实是一个定理,可以用最小自然数集原理+反证法证明。
…
牛爵士
莱布尼茨
-
微积分漫谈之一–微积分是如何出现的?(1)47
https://zhuanlan.zhihu.com/p/1919782810782270104 -
微积分漫谈之一–微积分是如何出现的?(2)11
https://zhuanlan.zhihu.com/p/1920107754481250596 -
微积分漫谈之一–微积分是如何出现的?(3)14
https://zhuanlan.zhihu.com/p/1920560030236808474 -
微积分漫谈之一–微积分是如何出现的?(4)24
https://zhuanlan.zhihu.com/p/1923755133872874043 -
微积分概述之二-牛顿留下的两个巨坑38
https://zhuanlan.zhihu.com/p/11757122419 -
微积分概述之三-艰难的填坑大业(1)4
https://zhuanlan.zhihu.com/p/1924070237126516767

- 微积分概述之三-艰难的填坑大业(2)极限定义的演变17
https://zhuanlan.zhihu.com/p/1926013591271749268
发布于 2025-07-26 16:37
via:
-
你也能懂的微积分
https://zhuanlan.zhihu.com/p/94592123 -
进一步了解「微积分」的书籍资料
https://mp.weixin.qq.com/s/wHc5y5ghoCVzMOtfOsVgDw -
微积分体系几百年前就建立起来了,为什么我们现在学习它仍存在困难? - 知乎
https://www.zhihu.com/question/435369583
