C语言---函数的递归与迭代
递归的理解与限制条件
所谓函数递归就是递推加回归的过程,就是函数自己调用自己。递归的思想就是把复杂的问题拆分成与原来那个大问题相似的子问题来求解,大事化小,像剥洋葱一样,最终把问题解决。
递归的限制条件:
一个递归程序,除了处理问题的递归主体之外,肯定是有递归的出口的(也就是递归的限制条件),每一次递归都是在栈区上给函数开辟一块空间,没有出口也就意味着栈没有销毁,最终会导致栈溢出的问题。所以每一次递归都要更加的接近这个限制条件才行。
递归举例
问题1:求n的阶乘。
问题分析:首先要知道什么是阶乘,就比如 5!= 5 * 4 * 3 * 2 * 1 ,就是一个数从自己本身,一直累乘到1。那么这个就可以用递归来解决,假设我们就求5的阶乘。
5! = 5 * 4 * 3 * 2 * 1
可以看成 5! = 5 * 4!
而4! = 4 * 3!
...................
从上边的分析就可以得出一个递归的公式
n! = n * (n - 1)! (由这个公式,我们就可以设计出一个计算 n! 的函数)
又因为 0! = 1,所以可以把这个设置成递归的出口。
代码实现:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>//Fact函数用于计算n的阶乘
int Fact(int n)
{if (n == 0)return 1;elsereturn n * Fact(n - 1);
}int main()
{int number = 0;scanf("%d", &number);int res = Fact(number);printf("%d\n", res);return 0;
}画图理解:
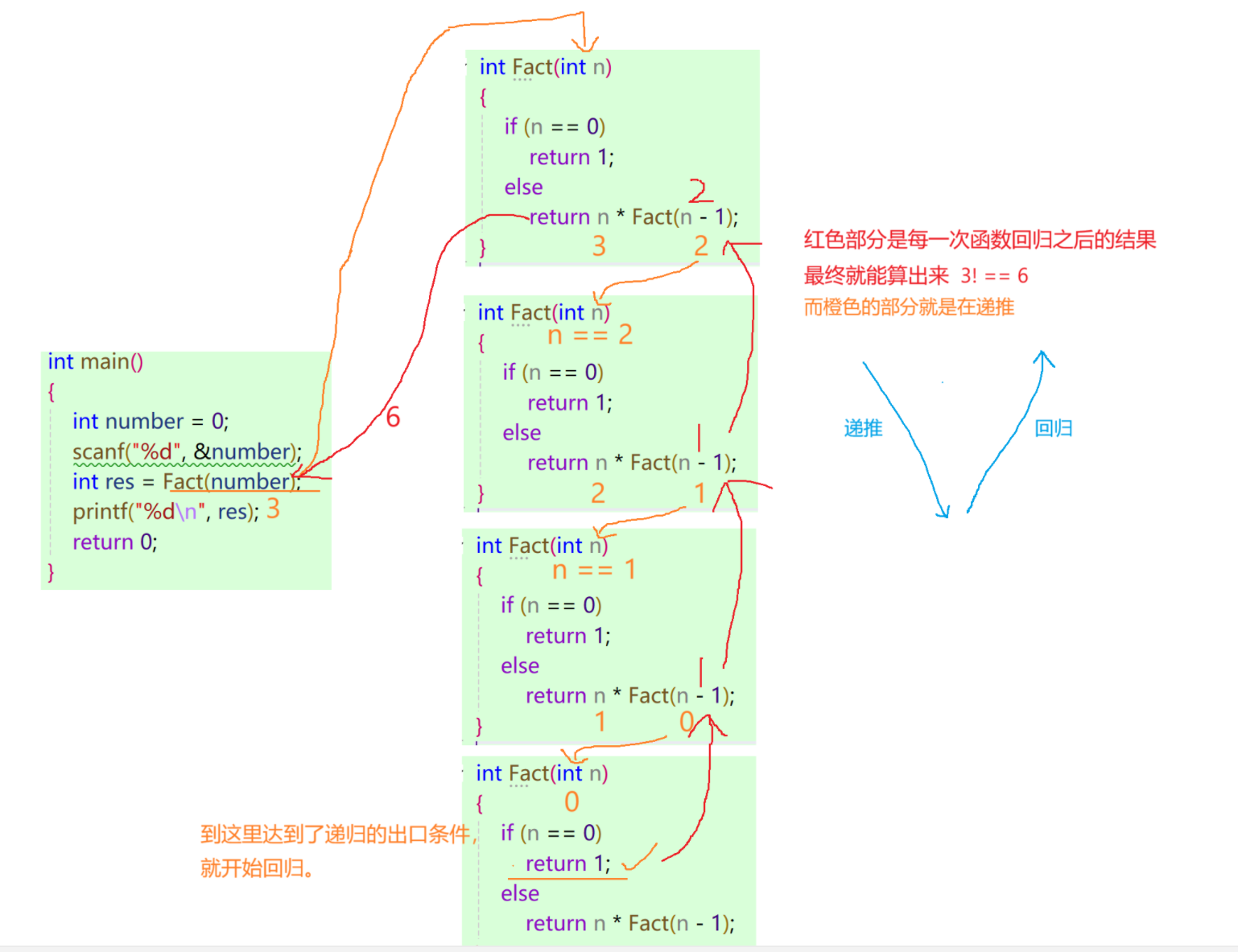
问题2:顺序打印一个整数的每一位。
问题分析:假设现在有一个数字为1234,我想要顺序打印它的每一位,就是依次打印 1 2 3 4。我们如果想要直接获取到1,然后打印,这是非常困难的,但是,获取到最后一位的4很容易,只需要 1234 % 10 就可以了,又由于我现在想要顺序打印,所以4是要最后打印的,那就可以先打印前边的123,再打印4,而打印123,又可以拆分为先打印12,再打印3.............就是一个递归
假设Print是我们自己设计的一个函数,专门用来顺序打印数字的
那么上边的思路就转化如下:
--> Print(1234) --> Print(123) + 4;
--> Print(123) --> Print(12) + 3;
--> Print(12) --> Print(1) + 2;
--> Print(1) --> 1(直接打印)
并且123,12......都是由原来的数字 num / 10 得到的
而由上边的分析就可以知道递归的出口就是当打印的数字为一位数的时候,就直接打印。
如果打印的数字是两位数,就先打印前边的数字,再打印最后一位的数字。
代码实现:
#include<stdio.h>
void Print(int n)
{if (n > 9)//大于9就说明是超过一位的,需要递归处理{Print(n / 10);printf("%d ", n % 10);//获取n的最后一位,并且是最后打印}elseprintf("%d ", n);//如果只有一位,直接打印
}int main()
{int num = 0;scanf("%d", &num);Print(num);return 0;
}
画图理解:
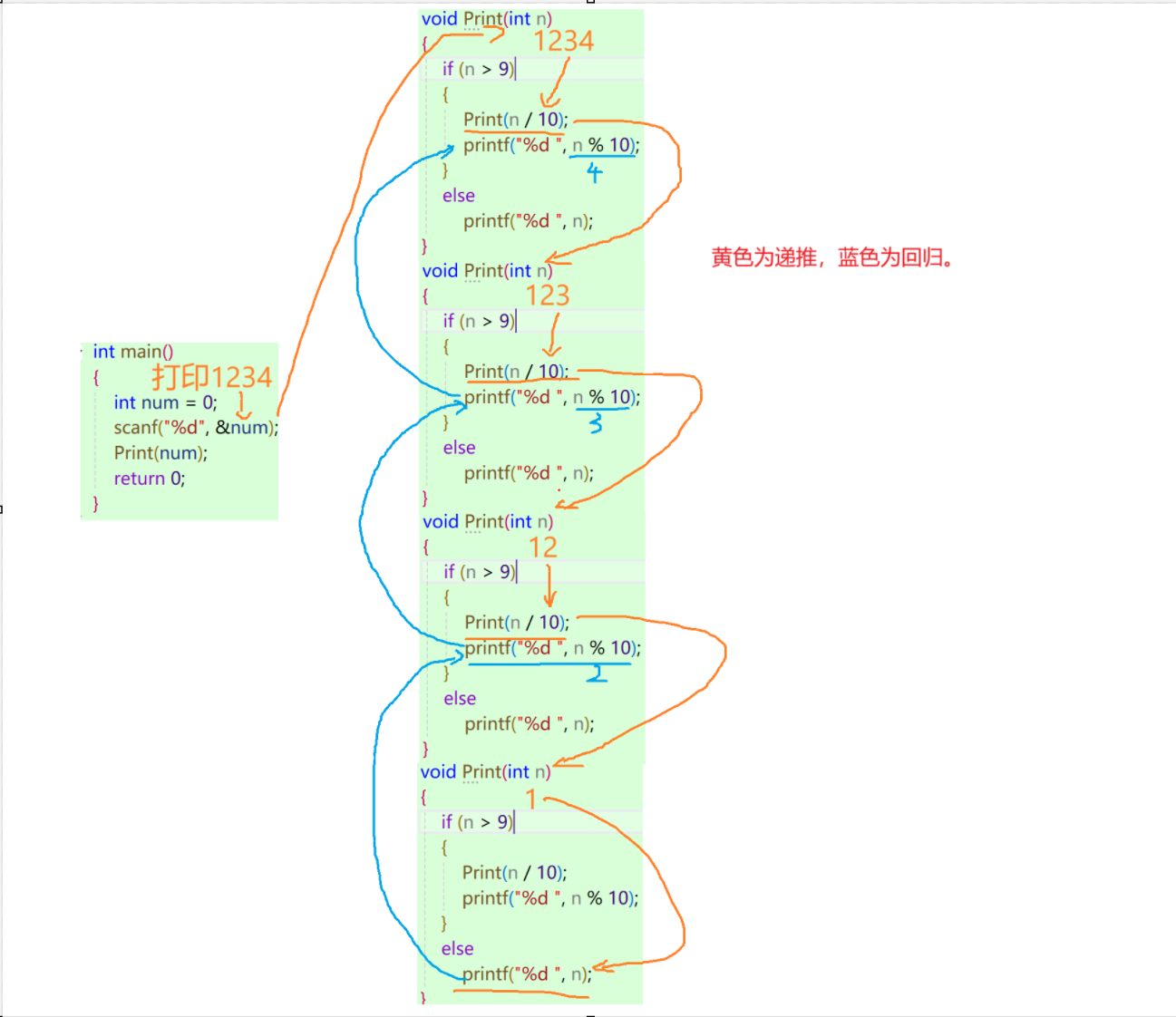
再注意一个点,就是这里的Print函数是没有返回值的其实,但是得先Print函数调用结束之后才会执行下边的代码,这也叫回归。
问题3:求第n个斐波那契数
问题分析:所谓斐波那契数就是 1 1 2 3 5 8 13 21 34............其实这里的规律很容易被发现,就是从第三个数字开始,后一个数字是由前两个数字加起来。而第一个和第二个斐波那契数,我们就可以把它看做是函数的递归出口。
代码实现:
#include<stdio.h>
//Fib(n)就表示的是第n个斐波那契数
int Fib(int n)
{if (n == 1 || n == 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}int main()
{int num = 0;scanf("%d", &num);printf("%d\n", Fib(num));return 0;
}附加:
还有两个问题之前已经写过了,是青蛙跳台阶和汉诺塔问题。链接如下。
用C语言函数递归实现青蛙跳台阶和汉诺塔问题-CSDN博客
递归与迭代
在上边就提到过函数递归如果从来没有递归出口的话就会导致栈溢出的问题,同样的,就算有递归出口,如果递归的层次太深,也会导致栈溢出。
如果不用递归的方式,迭代也是很好的解决方式,迭代通常就是由循环来实现的。它们俩是相辅相成的,不过迭代相对来说消耗的栈空间较少。效率要高一点。
迭代举例
问题1:用迭代的方式实现n的阶乘。
问题分析:刚才已经说了,迭代其实就是用循环来实现的,求n的阶乘可以先循环产生1~n之间的每一个数字,然后再累乘起来。
代码实现:
#include<stdio.h>
int main()
{int res = 1;//res用来存最后的结果,初始化为1是因为便于下边直接累乘int num = 0;scanf("%d", &num);//for循环产生1~num的数字for (int i = 1; i <= num; i++){res *= i;}printf("%d\n", res);return 0;
}问题2:用迭代的方式求第n个斐波那契数
问题分析:关于斐波那契数的定义已经在上边的递归里边讲到了。但是如果用递归求第50个斐波那契数的话,我们就会明显的发现,递归的结果迟迟没有出现,这就是上边提到的递归的层次太深了,会影响效率。
用迭代的方式:
为了计算第n个斐波那契数,我们可以先定义三个变量。
int a = 1;
int b = 1;
int c = 1;//这是第三个数字,用来最后返回的结果
根据斐波那契数列的规律,c可以通过a + b来实现,然后再把a的值改为b原来的值,b的值改为c的值,而现在的c就又可以由a+b来计算了,以此迭代下去,效果如下。
下边红色代表斐波那契数,而黑色就代表该数是第几个斐波那契数。
1 1 2 3 5 8 13 21.......
1 2 3 4 5 6 7 8.........
a b c..........................
a b c.......................
最后解释一下为什么c为1,因为如果要求的是第1或者第2个斐波那契数,就不会进入循环,所以直接初始化为1,具体大家可以看下边的代码。
代码实现:
#include<stdio.h>
int Fib(int n)
{int a = 1;int b = 1;int c = 1;//计算第三个斐波那契数及之后的数才进入循环//另外,找规律可以发现// 计算第3个斐波那契数只要计算一次// 计算第4个斐波那契数要计算两次.............while(n>=3){c = a + b;a = b;b = c;n--;}return c;
}int main()
{int num = 0;scanf("%d", &num);printf("%d\n", Fib(num));return 0;
}