当前位置：首页 > news >正文

关于Sort的补充

news 2025/8/3 14:43:50

前言：数据结构之排序-CSDN博客

一.快速排序的深入优化探讨

决定快排性能的关键点是每次单趟排序后，key对数组的分割，如果每次选key基本⼆分居中，那么快排的递归树就是颗均匀的满⼆叉树，性能最佳。但是实践中虽然不可能每次都是⼆分居中，但是性能也还是可控的。但是如果出现每次选到最⼩值/最⼤值，划分为0个和N-1的⼦问题时，时间复杂度为O(N^2)，数组序列有序时就会出现这样的问题，我们前⾯已经⽤三数取中或者随机选key解决了这个问题，也就是说我们解决了绝⼤多数的问题，但是现在还是有⼀些场景没解决(数组中有⼤量重复数据时)，也会影响快排的性能问题，所以我们需要引入一种新的快排方式——三路划分。

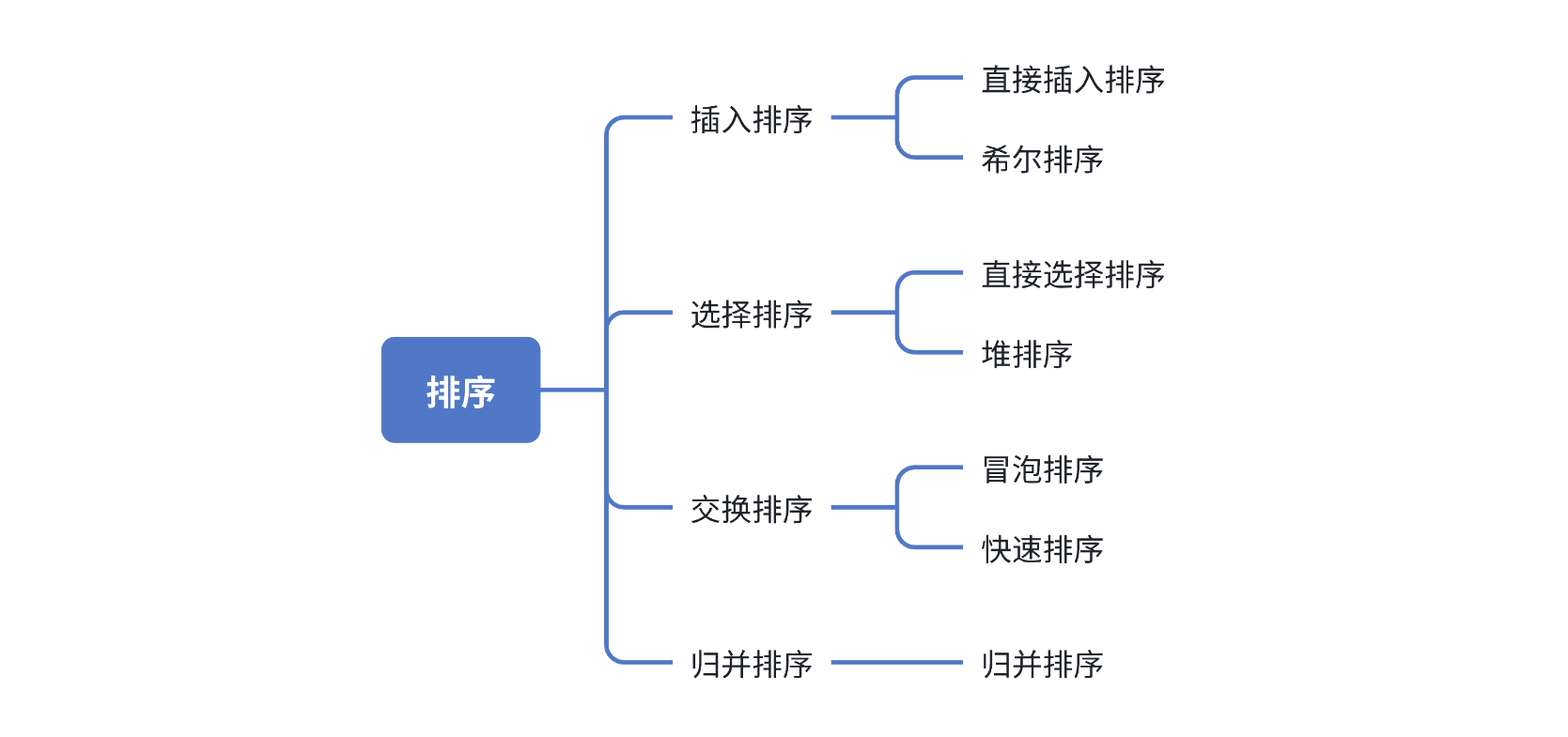
1.三路划分

三路划分算法解析：

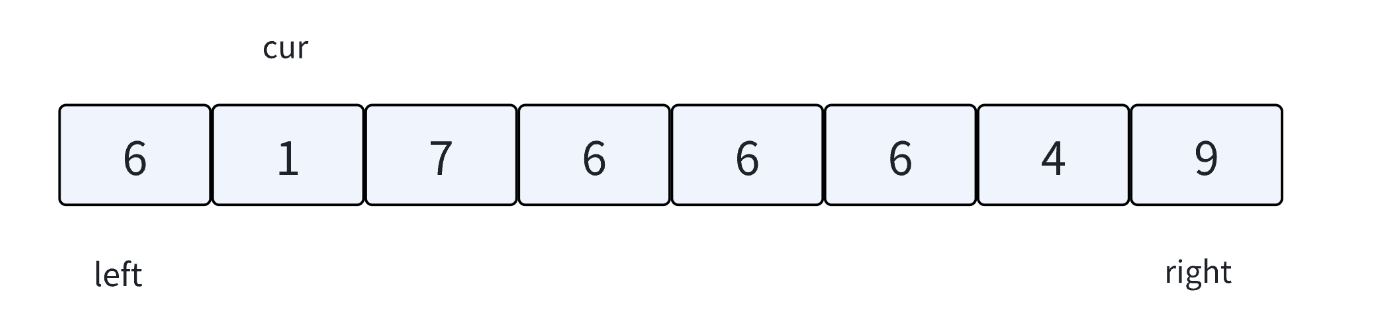
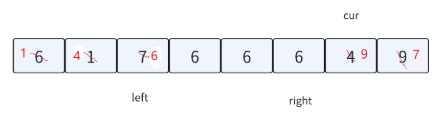
当⾯对有⼤量跟key相同的值时，三路划分的核⼼思想有点类似hoare的左右指针和lomuto的前后指针的结合。核⼼思想是把数组中的数据分为三段【⽐key⼩的值】【跟key相等的值】【⽐key⼤的值】，所以叫做三路划分算法。结合下图，理解⼀下实现思想：

1. key默认取left位置的值。

2. left指向区间最左边，right指向区间最后边，cur指向left+1位置。

3. cur遇到⽐key⼩的值后跟left位置交换，换到左边，left++，cur++。

4. cur遇到⽐key⼤的值后跟right位置交换，换到右边，right--。

5. cur遇到跟key相等的值后，cur++。

6. 直到cur > right结束。

可以自己模拟一下整个过程。

代码实现：

void QuickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left;int end = right;// 随机选keyint randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);// 三路划分// left和right指向就是跟key相等的区间// [begin, left-1] [left, right] right+1, end]int key = a[left];int cur = left + 1;while (cur <= right){// 1、cur遇到⽐key⼩，⼩的换到左边，同时把key换到中间位置// 2、cur遇到⽐key⼤，⼤的换到右边if (a[cur] < key){Swap(&a[cur], &a[left]);++left;++cur;}else if (a[cur] > key){Swap(&a[cur], &a[right]);--right;}else{++cur;}}// [begin, left-1] [left, right] right+1, end]QuickSort(a, begin, left - 1);QuickSort(a, right + 1, end);
}

912. 排序数组 - 力扣（LeetCode）

这个OJ，当我们⽤快排的时候，传统的hoare和lomuto（双指针）的⽅法，都过不了这个题⽬。堆排序和归并和希尔是可以过的，其他⼏个O(N^2)也不过了，因为这个题的测试⽤例中不仅仅有数据很多的⼤数组，也有⼀些特殊数据的数组，如⼤量重复数据的数组。堆排序和归并和希尔不是很受数据样本的分布和形态的影响，但是快排会，因为快排要选key，每次key都当趟分割都很偏，就会出现效率退化问题。

使用三路划分的方法。

测试代码：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void QuickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left;int end = right;// 随机选keyint randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);// 三路划分// left和right指向就是跟key相等的区间// [begin, left-1] [left, right] right+1, end]int key = a[left];int cur = left + 1;while (cur <= right){// 1、cur遇到⽐key⼩，⼩的换到左边，同时把key换到中间位置// 2、cur遇到⽐key⼤，⼤的换到右边if (a[cur] < key){Swap(&a[cur], &a[left]);++left;++cur;}else if (a[cur] > key){Swap(&a[cur], &a[right]);--right;}else{++cur;}}// [begin, left-1] [left, right] right+1, end]QuickSort(a, begin, left - 1);QuickSort(a, right + 1, end);
}int* sortArray(int* nums, int numsSize, int* returnSize) {srand(time(0));QuickSort(nums, 0, numsSize - 1);*returnSize = numsSize;return nums;
}

2.introspective sort（自省排序）

introspective sort是另一种解决快排深度太深导致性能下降的方法，这个方法的思路就是进行自我侦测和反省，快排递归深度太深（sgi stl中使⽤的是深度为2倍排序元素数量的对数值）那就说明在

这种数据序列下，选key出现了问题，性能在快速退化，那么就不要再进⾏快排分割递归了，改换为堆排序进⾏排序。

代码实现：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩⼦中⼤的那⼀个if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{// 建堆 -- 向下调整建堆 -- O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// ⾃⼰先实现 -- O(N*logN)int end = n - 1;while (end > 0){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);--end;}
}
void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i - 1;int tmp = a[i];// 将tmp插⼊到[0,end]区间中，保持有序while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}void IntroSort(int* a, int left, int right, int depth, int defaultDepth)
{if (left >= right)return;// 数组⻓度⼩于16的⼩数组，换为插⼊排序，简单递归次数if (right - left + 1 < 16){InsertSort(a + left, right - left + 1);return;}// 当深度超过2*logN时改⽤堆排序if (depth > defaultDepth){HeapSort(a + left, right - left + 1);return;}depth++;int begin = left;int end = right;// 随机选keyint randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end]IntroSort(a, begin, keyi - 1, depth, defaultDepth);IntroSort(a, keyi + 1, end, depth, defaultDepth);
}
void QuickSort(int* a, int left, int right)
{int depth = 0;int logn = 0;int N = right - left + 1;for (int i = 1; i < N; i *= 2){logn++;}// introspective sort -- ⾃省排序IntroSort(a, left, right, depth, logn * 2);
}

这里主要引入了depth计算递归深度，当depth > logn * 2 时候，会改用堆排，也引入了小区间优化，数组⻓度⼩于16的⼩数组，换为插⼊排序，简单递归次数。关于为什么是depth > logn * 2，而不是logn或者logn * 3，只能说明ogn * 2是一个比较适中的值，logn、logn * 3也没有问题。

测试代码：可以自行测试不同倍数logn的情况。

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩⼦中⼤的那⼀个if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{// 建堆 -- 向下调整建堆 -- O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// ⾃⼰先实现 -- O(N*logN)int end = n - 1;while (end > 0){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);--end;}
}
void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i - 1;int tmp = a[i];// 将tmp插⼊到[0,end]区间中，保持有序while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}void IntroSort(int* a, int left, int right, int depth, int defaultDepth)
{if (left >= right)return;// 数组⻓度⼩于16的⼩数组，换为插⼊排序，简单递归次数if (right - left + 1 < 16){InsertSort(a + left, right - left + 1);return;}// 当深度超过2*logN时改⽤堆排序if (depth > defaultDepth){HeapSort(a + left, right - left + 1);return;}depth++;int begin = left;int end = right;// 随机选keyint randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end]IntroSort(a, begin, keyi - 1, depth, defaultDepth);IntroSort(a, keyi + 1, end, depth, defaultDepth);
}
void QuickSort(int* a, int left, int right)
{int depth = 0;int logn = 0;int N = right - left + 1;for (int i = 1; i < N; i *= 2){logn++;}// introspective sort -- ⾃省排序IntroSort(a, left, right, depth, logn * 2);
}
int* sortArray(int* nums, int numsSize, int* returnSize) {srand(time(0));QuickSort(nums, 0, numsSize - 1);* returnSize = numsSize;return nums;
}

二.外排序之文件归并排序实现

外排序（External sorting）是指能够处理极⼤量数据的排序算法。通常来说，外排序处理的数据不能⼀次装⼊内存，只能放在读写较慢的外存储器(通常是硬盘)上。外排序通常采⽤的是⼀种“排序-归并”的策略。在排序阶段，先读⼊能放在内存中的数据量，将其排序输出到⼀个临时⽂件，依此进⾏，将待排序数据组织为多个有序的临时⽂件。然后在归并阶段将这些临时⽂件组合为⼀个⼤的有序⽂件，也即排序结果。

跟外排序对应的就是内排序，我们之前讲的常⻅的排序，都是内排序，他们排序思想适应的是数据在内存中，⽀持随机访问。归并排序的思想不需要随机访问数据，只需要依次按序列读取数据，所归并排序既是⼀个内排序，也是⼀个外排序。

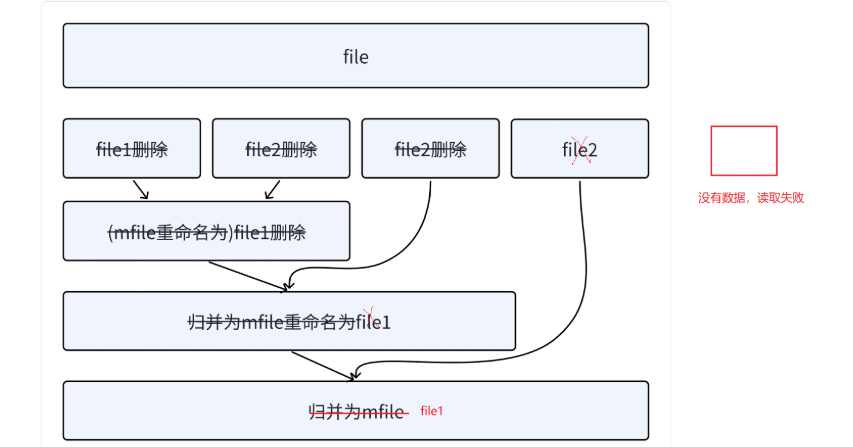
1.⽂件归并排序思路分析

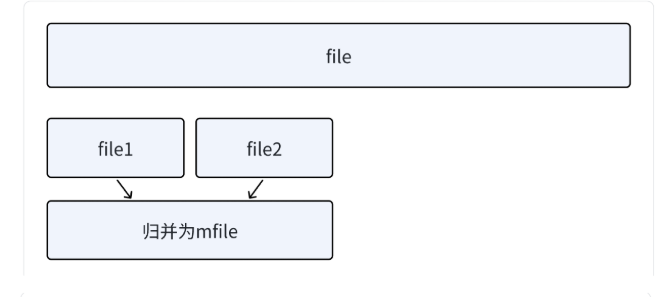
1. 读取n个值排序后写到file1，再读取n个值排序后写到file2。

2. file1和file2利⽤归并排序的思想，依次读取⽐较，取⼩的尾插到mfile，mfile归并为⼀个有序⽂件。

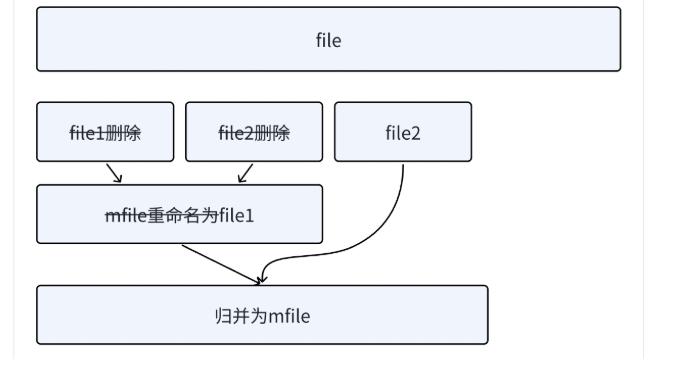
3. 将file1和file2删掉，mfile重命名为file1。

4. 再次读取n个数据排序后写到file2。

5. 继续⾛file1和file2归并，重复步骤2，直到⽂件中⽆法读出数据。最后归并出的有序数据放到了

file1中。

代码实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<time.h>
#include<stdlib.h>// 创建N个随机数，写到文件中
void CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = rand() + i;fprintf(fin, "%d\n", x);}fclose(fin);
}int compare(const void* a, const void* b)
{return (*(int*)a - *(int*)b);
}// 返回实际读到的数据个数，没有数据了，返回0
int ReadNDataSortToFile(FILE* fout, int n, const char* file1)
{int x = 0;int* a = (int*)malloc(sizeof(int) * n);if (a == NULL){perror("malloc error");return 0;}// 想读取n个数据，如果遇到文件结束，应该读到j个int j = 0;for (int i = 0; i < n; i++){if (fscanf(fout, "%d", &x) == EOF)break;a[j++] = x;}if (j == 0){free(a);return 0;}// 排序qsort(a, j, sizeof(int), compare);FILE* fin = fopen(file1, "w");if (fin == NULL){free(a);perror("fopen error");return 0;}// 写回file1文件for (int i = 0; i < j; i++){fprintf(fin, "%d\n", a[i]);}free(a);fclose(fin);return j;
}void MergeFile(const char* file1, const char* file2, const char* mfile)
{FILE* fout1 = fopen(file1, "r");if (fout1 == NULL){perror("fopen error");return;}FILE* fout2 = fopen(file2, "r");if (fout2 == NULL){perror("fopen error");return;}FILE* mfin = fopen(mfile, "w");if (mfin == NULL){perror("fopen error");return;}// 归并逻辑int x1 = 0;int x2 = 0;int ret1 = fscanf(fout1, "%d", &x1);int ret2 = fscanf(fout2, "%d", &x2);while (ret1 != EOF && ret2 != EOF){if (x1 < x2){fprintf(mfin, "%d\n", x1);ret1 = fscanf(fout1, "%d", &x1);}else{fprintf(mfin, "%d\n", x2);ret2 = fscanf(fout2, "%d", &x2);}}while (ret1 != EOF){fprintf(mfin, "%d\n", x1);ret1 = fscanf(fout1, "%d", &x1);}while (ret2 != EOF){fprintf(mfin, "%d\n", x2);ret2 = fscanf(fout2, "%d", &x2);}fclose(fout1);fclose(fout2);fclose(mfin);
}int main()
{CreateNDate();const char* file1 = "file1.txt";const char* file2 = "file2.txt";const char* mfile = "mfile.txt";FILE* fout = fopen("data.txt", "r");if (fout == NULL){perror("fopen error");return;}int m = 1000000;ReadNDataSortToFile(fout, m, file1);ReadNDataSortToFile(fout, m, file2);while (1){MergeFile(file1, file2, mfile);// 删除file1和file2remove(file1);remove(file2);// 重命名mfile为file1rename(mfile, file1);// 当再去读取数据，一个都读不到，说明已经没有数据了// 已经归并完成，归并结果在file1int n = 0;if ((n = ReadNDataSortToFile(fout, m, file2)) == 0)break;}return 0;
}

注意：需要先CreateNDate，产生文件后再归并。

查看全文

http://www.dtcms.com/a/312159.html