当前位置： 首页 > news >正文

二叉树链式结构的实现

news 2025/8/3 12:56:55

1 前置说明

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在对二叉树结构掌握还不够深入，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，之后再来系统的研究二叉树真正的创建方式。

typedef int BTDataType;
typedef struct BinaryTreeNode
{//节点数据BTDataType data;//左右孩子struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BT;BT* BuyNode(int x)
{//扩容BT* node = (BT*)malloc(sizeof(BT));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}BT* CreatBinaryTree()
{//节点赋值BT* node1 = BuyNode(1);BT* node2 = BuyNode(2);BT* node3 = BuyNode(3);BT* node4 = BuyNode(4);BT* node5 = BuyNode(5);BT* node6 = BuyNode(6);//链接节点node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树
2. 非空：根结点，根结点的左子树、根结点的右子树组成的。

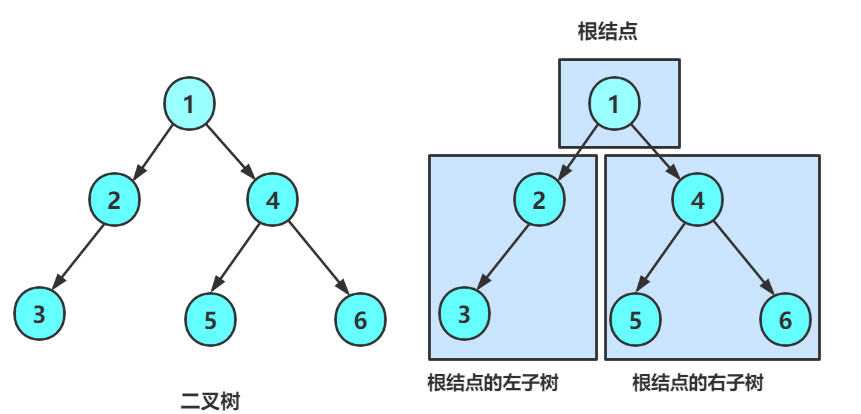
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

2 前序遍历

2.1 代码

//前序遍历
void PrevOrder(BT* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);//递归访问PrevOrder(root->left);PrevOrder(root->right);
}

 2.2 输出结果以及验证

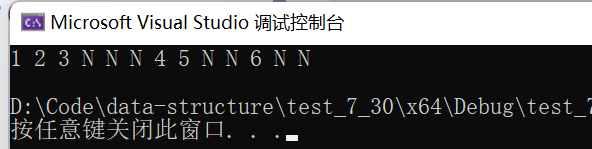
2.3 执行过程 

  1. 类型定义阶段：

    • 首先执行typedef int BTDataType，将int类型重命名为BTDataType
    • 接着定义struct BinaryTreeNode结构体，并通过typedef重命名为BT，完成二叉树节点的类型定义

  2. 调用CreatBinaryTree函数创建二叉树：

    • 函数内部依次调用BuyNode(1)到BuyNode(6)创建 6 个节点：
      • 每个BuyNode调用都会：分配内存→检查分配结果→初始化数据和指针→返回节点地址
    • 节点创建完成后，建立链接关系：
      • node1->left = node2（1 的左孩子是 2）
      • node1->right = node4（1 的右孩子是 4）
      • node2->left = node3（2 的左孩子是 3）
      • node4->left = node5（4 的左孩子是 5）
      • node4->right = node6（4 的右孩子是 6）
    • 最后返回根节点node1的地址

  3. 调用PrevOrder函数进行前序遍历（以根节点node1为参数）：

    • 第一层递归（root=node1）：
      • 输出1
      • 调用PrevOrder(node1->left)（即 node2）
    • 第二层递归（root=node2）：
      • 输出2
      • 调用PrevOrder(node2->left)（即 node3）
    • 第三层递归（root=node3）：
      • 输出3
      • 调用PrevOrder(node3->left)（即 NULL）→输出N 并返回
      • 调用PrevOrder(node3->right)（即 NULL）→输出N 并返回
      • 返回到第二层
    • 第二层继续：
      • 调用PrevOrder(node2->right)（即 NULL）→输出N 并返回
      • 返回到第一层
    • 第一层继续：
      • 调用PrevOrder(node1->right)（即 node4）
    • 第二层递归（root=node4）：
      • 输出4
      • 调用PrevOrder(node4->left)（即 node5）
    • 第三层递归（root=node5）：
      • 输出5
      • 调用PrevOrder(node5->left)（即 NULL）→输出N 并返回
      • 调用PrevOrder(node5->right)（即 NULL）→输出N 并返回
      • 返回到第二层
    • 第二层继续：
      • 调用PrevOrder(node4->right)（即 node6）
    • 第三层递归（root=node6）：
      • 输出6
      • 调用PrevOrder(node6->left)（即 NULL）→输出N 并返回
      • 调用PrevOrder(node6->right)（即 NULL）→输出N 并返回
      • 返回到第二层，再返回到第一层
    • 遍历结束，最终输出结果：1 2 3 N N N 4 5 N N 6 N N

整个过程从类型定义开始，先创建节点并构建二叉树结构，最后通过递归实现前序遍历并输出结果。

2.4 逻辑过程（程序执行的逻辑流程）

  1. 类型定义与函数声明

    • 逻辑上先完成数据类型的抽象定义：通过typedef将int定义为BTDataType（数据类型抽象），定义BinaryTreeNode结构体（描述二叉树节点的逻辑结构：包含数据域和左右孩子指针），并简化命名为BT。
    • 声明BuyNode、CreatBinaryTree、PrevOrder三个函数，确定函数的输入输出逻辑。

  2. 二叉树的构建逻辑

    • 节点创建：BuyNode函数的逻辑是 “输入一个值→申请内存→初始化节点（数据赋值、指针置空）→返回节点”，封装了单个节点的创建逻辑。
    • 树结构构建：CreatBinaryTree函数通过逻辑步骤构建树：先创建 6 个独立节点（值 1-6），再通过指针赋值建立节点间的父子关系（如node1->left = node2表示 1 的左孩子是 2），最终形成一个固定结构的二叉树，逻辑上确定了树的拓扑关系。

  3. 前序遍历的逻辑流程

  • 遵循 “根→左→右” 的递归逻辑：
  • 若当前节点为NULL，逻辑上表示 “空节点”，输出N ；
  • 否则先输出当前节点数据，再递归处理左子树（逻辑上的 “左”），最后递归处理右子树（逻辑上的 “右”）；
  • 通过递归调用，将整棵树的遍历拆解为单个节点的处理逻辑，最终按前序顺序输出所有节点（包括空节点）。

2.5 物理过程（程序在计算机中的实际执行操作）

  1. 编译与内存分配

    • 编译阶段：类型定义和函数声明被编译器解析，确定BT类型的内存大小（int数据 + 两个指针，通常为 16 字节，取决于系统）。
    • 运行时：
      • BuyNode函数调用malloc(sizeof(BT))，向操作系统申请一块连续的内存（物理地址上的一块空间），用于存储节点数据；
      • 若申请成功，通过指针node指向该内存块，然后将参数x写入数据域，将左右指针域物理地址设为0（NULL的物理表示）。

  2. 二叉树的物理存储

    • 6 个节点通过BuyNode分别在内存中占据独立的物理块（地址不连续）；
    • CreatBinaryTree中的指针赋值（如node1->left = node2），本质是将node2的物理内存地址写入node1的左指针域，通过物理地址的关联形成 “树结构”（逻辑上的父子关系对应物理上的地址指向）。

  3. 前序遍历的物理执行

    • 递归调用时，每次调用PrevOrder会在栈内存中创建函数栈帧（存储参数root的物理地址、返回地址等）；
    • 访问root->data时，通过root存储的物理地址找到节点内存块，读取其中的数据域并输出；
    • 递归访问左 / 右子树时，实际是将左 / 右指针存储的物理地址作为新参数压入栈，重复上述过程；
    • 当root为NULL（物理地址0），输出N 并弹出当前栈帧，返回上一层调用。

  4. 最终结果的物理表现

    • 所有输出操作通过标准输出流（如控制台）将字符序列1 2 3 N N N 4 5 N N 6 N N 物理地显示在设备上，完成整个过程。

总结

  • 逻辑过程：关注 “做什么”，即数据结构的定义、函数的逻辑步骤、递归的执行顺序等抽象流程。
  • 物理过程：关注 “怎么做”，即内存的分配与释放、指针的地址指向、栈帧的创建与销毁、数据在硬件上的读写等实际操作。

物理上空间是可以重复利用的。

需要注意的是无限向下递归（树的深度太深），则会导致栈溢出的问题。 

3 中序遍历

3.1 代码

//中序遍历
void InOrder(BT* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

 3.2 输出结果及其验证

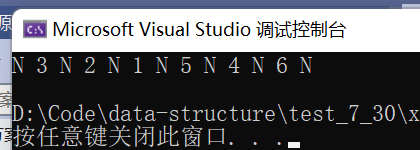
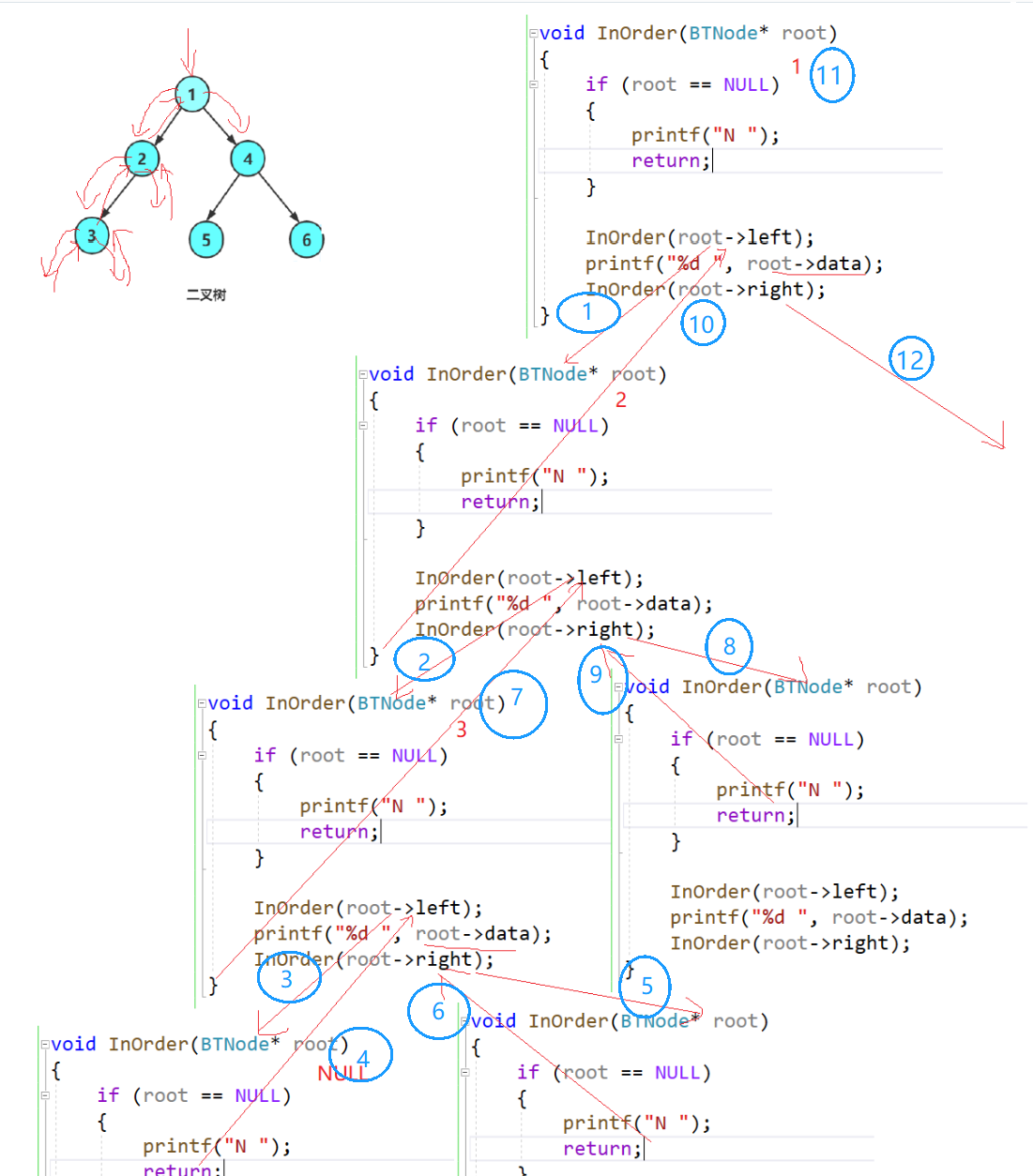
3.3  执行过程

圈起来的数据，表示次序。

4 计算节点个数

4.1 统计二叉树的节点总数

错误代码：

运行结果： 

因为在这个过程中，局部静态，初始化0，只会被执行一次，下一次调用的时候，就不能为0了，会在之前的结果上面累加。所以，不可以用静态问题解决。

所以：

//正确 求个数
int TreeSize(BT* root)
{return root == NULL ? 0 :TreeSize(root->left) + TreeSize(root->right) + 1;
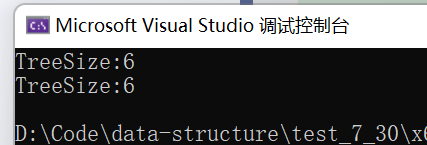
}int main()
{BT* root = CreatBinaryTree();printf("TreeSize:%d\n", TreeSize(root));printf("TreeSize:%d\n", TreeSize(root));return 0;
}

思路：

  • 功能目标：计算二叉树中所有节点（包括根、内部节点、叶子节点）的总数量。
  • 分解逻辑：
    • 空树（root == NULL）的节点数为 0；
    • 非空树的节点数 = 1（当前根节点） + 左子树的节点数 + 右子树的节点数。

4.2 统计二叉树的叶子节点数

//统计二叉树的叶子节点数
int TreeLeafSize(BT* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left)+ TreeLeafSize(root->right);
}

思路：

  • 功能目标：计算二叉树中 “左右孩子均为空” 的节点（叶子节点）数量。
  • 分解逻辑：
    • 空树的叶子数为 0；
    • 若当前节点是叶子（left == NULL && right == NULL），则贡献 1 个叶子；
    • 非叶子节点的叶子数 = 左子树的叶子数 + 右子树的叶子数（当前节点不贡献叶子）。

4.3 计算二叉树的高度

//计算二叉树的高度
int TreeHeight(BT* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}

思路：

  • 功能目标：计算二叉树的最大深度（从根到最远叶子节点的边数 + 1，或节点层数）。
  • 分解逻辑：
    • 空树的高度为 0；
    • 非空树的高度 = 1（当前节点所在层） + 左右子树中较高者的高度（取最大值保证是 “最远叶子”）。

这是「递归的核心」：把当前节点的左、右子树当成独立的小树，分别计算它们的高度。

以示例树为例：

  • 计算根节点 1 的左子树（节点 2）的高度：
    • 节点 2 的左子树是节点 4，节点 4 的左右子树都是NULL
    • 所以TreeHeight(节点4)的结果是 1（自身 1 层 + 左右子树高度 0）
    • 因此TreeHeight(节点2) = 1（自身） + TreeHeight(节点4)（1） = 2
  • 计算根节点 1 的右子树（节点 3）的高度：
    • 节点 3 的左右子树都是NULL
    • 所以TreeHeight(节点3) = 1（自身 1 层 + 左右子树高度 0）

 计算当前节点的高度

  • 逻辑：当前节点的高度 = 自身这一层（+1） + 左右子树中「更高的那个子树的高度」
  • 为什么取最大值？因为高度要算「最远」的叶子节点，所以选更高的一边。

以示例树为例：

  • 根节点 1 的左子树高度是 2（节点 2 的高度），右子树高度是 1（节点 3 的高度）
  • 取最大值 2，加 1（自身层），得到 3 → 这就是整棵树的高度
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;

这是三目运算符，等价于下面的 if-else 逻辑：

if (leftHeight > rightHeight) {// 左子树更高，当前节点高度 = 左子树高度 + 自身这一层return leftHeight + 1;
} else {// 右子树更高（或相等），当前节点高度 = 右子树高度 + 自身这一层return rightHeight + 1;
}

这句代码的作用是 ——在左右子树中选更高的那个高度，再加上当前节点自己这一层，就是当前节点的高度。

为什么要加 1？

"+1" 是因为当前节点自身也算一层。
比如：

  • 如果一个节点的左子树高度是 2（意味着左子树有 2 层），右子树高度是 1
  • 那么从当前节点往下数，最深能到左子树的第 2 层，加上当前节点自己这一层，总高度就是 2 + 1 = 3

 想象你站在一棵二叉树的某个节点上，想知道从这个节点到它下方最深的叶子有多少层（这就是该节点的 "高度"）。

  • 你左边有一棵子树，高度是leftHeight（比如 3 层）
  • 你右边有一棵子树，高度是rightHeight（比如 2 层）
  • 那么你所在位置的高度 = 你自己这一层（+1） + 左右子树中更高的那个高度（选左边的 3 层）
  • 结果就是：3 + 1 = 4 层

所以： 

 

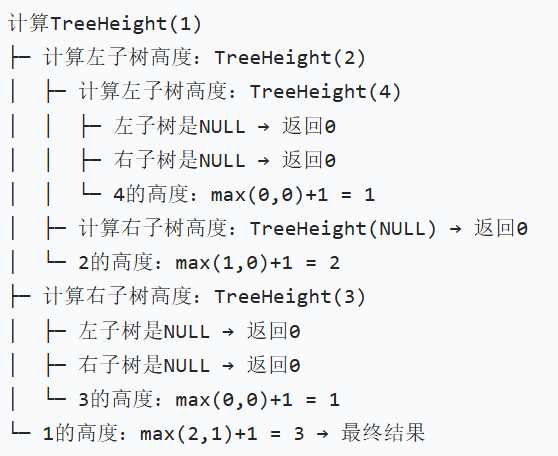
总结

这三个函数的编写思路高度统一：

  1. 利用二叉树的递归结构，将整体问题拆解为 “根节点处理”+“左右子树递归处理”；
  2. 明确空节点的边界条件，确保递归终止；
  3. 根据不同统计目标（节点总数 / 叶子数 / 高度），设计 “当前节点贡献值” 与 “子树结果” 的组合方式（累加 / 条件判断 / 取最大值）。

这种思路既符合二叉树的结构特性，又使代码简洁易懂，充分体现了递归在处理树结构问题时的优势。

运行一下：

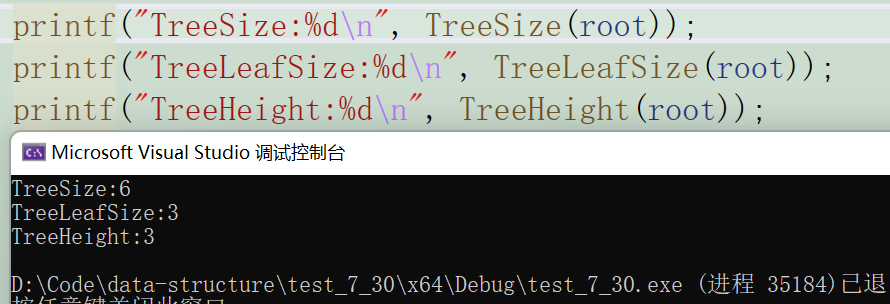
 注意：

不要

这样写，因为这段代码确实存在严重的效率问题，核心原因是对同一子树进行了冗余的递归计算，导致时间复杂度呈指数级增长，尤其在处理深度较大的树时，效率会极其低下。通过引入临时变量存储中间结果，可以彻底解决这个问题。

我们通过具体分析来理解：

问题根源：重复计算同一子树

假设我们要计算某个节点的高度，这段代码的执行逻辑是：

  1. 先调用TreeHeight(root->left)计算左子树高度（记为 A）；
  2. 再调用TreeHeight(root->right)计算右子树高度（记为 B）；
  3. 比较 A 和 B 的大小后，如果 A 更大，会再次调用TreeHeight(root->left)（又算一次 A），然后 + 1 返回；
    同理，如果 B 更大，会再次调用TreeHeight(root->right)（又算一次 B），然后 + 1 返回。

也就是说，左子树或右子树会被计算 2 次（一次用于比较，一次用于最终结果）。

对效率的影响：呈指数级放大

以一棵简单的左斜树（每个节点只有左子树）为例：

计算根节点 1 的高度时：

  • 正常逻辑（用临时变量）：左子树只需计算 1 次，总递归次数为n；
  • 这段代码：左子树会被计算 2 次，而每个左子树的计算又会导致其下一层左子树被计算 2 次，最终总递归次数为2^n（指数级增长）。

当树的深度为 20 时，2^20约为 100 万次计算，而正常逻辑只需 20 次，效率差距悬殊。

所以用leftHeight和rightHeight存储子树高度，避免重复调用TreeHeight（如果直接写max(TreeHeight(left), TreeHeight(right))，会导致同一子树被计算两次，效率低）。

 

http://www.dtcms.com/a/312071.html

相关文章：

  • lesson31：Python异常处理完全指南：从基础到高级实践
  • 乌鸫科技前端二面
  • Go语言中的闭包详解
  • OpenCV学习 day3
  • stm32是如何实现电源控制的？
  • 如何防止内存攻击（Buffer Overflow, ROP）
  • 髋臼方向的定义与测量-I
  • u-boot启动过程（NXP6ULL）
  • android studio 安装Flutter
  • WD5208S，12V500MA，应用于小家电电源工业控制领域
  • Kubernetes 构建高可用、高性能 Redis 集群实战指南
  • #C语言——学习攻略：探索字符函数和字符串函数（一）--字符分类函数，字符转换函数，strlen，strcpy，strcat函数的使用和模拟实现
  • 数据库理论
  • 【MATLAB】（五）向量
  • 变量筛选—随机森林特征重要性
  • windows@Path环境变量中同名可执行文件优先级竞争问题@Scoop安装软件命令行启动存在同名竞争问题的解决
  • 解决 InputStream 只能读取一次问题
  • Java语言核心特性全解析：从面向对象到跨平台原理
  • Docker--将非root用户添加docker用户组，解决频繁sudo执行输入密码的问题
  • 【动态规划 | 子序列问题】子序列问题的最优解：动态规划方法详解
  • RK628F HDMI-IN调试：应用接口使用
  • Vulnhub ELECTRICAL靶机复现（附提权）
  • QPainter::CompositionMode解析
  • junit总@mockbaen与@mock的区别与联系
  • flutter分享到支付宝
  • Linux进程控制核心：创建·等待·终止·替换
  • Qt 信号和槽正常连接返回true，但发送信号后槽函数无响应问题【已解决】
  • 深入解析Java Stream Sink接口
  • Design Compiler：Milkyway库的创建与使用
  • 1-7〔 OSCP ◈ 研记 〕❘ 信息收集▸主动采集E：SMB基础