【MATLAB】(五)向量
一.向量的定义
向量是由n个数a1,a2,…,an组成的有序数组,记成
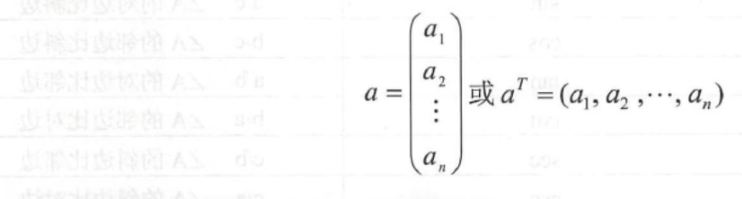
叫做n维向量,向量a的第i个分量称为ai。竖着成为列向量,横着成为行向量。
二.向量的生成方式
向量的生成:直接输入法、冒号法和利用MATLAB函数创建三种方法。
(1)直接输入法。
生成向量最直接的方法就是在命令行窗口中直接输入。格式上的要求如下:
①向量元素需要用“[ ]”括起来。
②元素之间可以用空格、逗号或分号分隔。
直接输入法中,可以用空格和逗号分隔生成行向量,用分号分隔形成列向量。
>> %生成一个行向量
>> a=[1,2,3]a =1 2 3>> a=[1 2 3]a =1 2 3>> %生成一个列向量
>> a=[1;2;3]a =123>> %生成一个矩阵
>> a=[1,2;3,4]a =1 23 4(2)冒号法。
基本格式是 x=first:increment:last,表示创建一个从 first 开始,到last 结束,数据元素的增量为increment 的向量。若增量为1,上面创建向量的方式简写为x=frst:last。
>> %生成一个行向量,从0开始,以10为步长,最后为100
>> a=0:10:100a =0 10 20 30 40 50 60 70 80 90 100>> %生成一个行向量,从0开始,以1为步长,最后为10
>> a=0:1:10a =0 1 2 3 4 5 6 7 8 9 10>> a=0:10a =0 1 2 3 4 5 6 7 8 9 10>> %若步长无法被结尾数字整除
>> a=0:3:10a =0 3 6 9>> %若步长大于范围最大值
>> a=0:100:10a =0>> %若步长为负数
>> a=0:-1:10a =空的 1×0 double 行向量>> a=10:-1:0a =10 9 8 7 6 5 4 3 2 1 0(3)利用函数linspace 创建向量。
linspace通过直接定义数据元素个数,而不是数据元素之间的增量来创建向量。此函数的调用格式如下:
linspace(first value,last value,number)
该调用格式表示创建一个从 first value 开始 last value 结束,包含 number 个元素的向量。
>> %0到10之间,有5个数,但是间隔只有4个,所以步长为(10-0)/4=2.5
>> x=linspace(0,10,5)x =0 2.5000 5.0000 7.5000 10.0000>> x=linspace(100,10,5)x =100.0000 77.5000 55.0000 32.5000 10.0000(4)利用函数logspace 创建一个对数分隔的向量。
与 linspace 一样,logspace 也通过直接定义向量元素个数,而不是数据元素之间的增量来创建数组。logspace 的调用格式如下。
logspace(first value,last value,number)
表示创建一个从 10^first_value开始,到 10^last_value 结束,包含 number 个数据元素的向量。
>> x=logspace(1,3,3)x =10 100 1000(5)行向量和列向量的相互转化。
基本方法是加一个“ ' ”。
>> a=[1,2,3]a =1 2 3>> b=a'b =123>> x=[1;2;3]x =123>> y=x'y =1 2 3三.向量中元素的引用
向量元素的引用方式如表所示。

>> x=0:1:10x =0 1 2 3 4 5 6 7 8 9 10(1)给定所取元素的下标,取出向量元素中该位置的元素
>>取出向量中的第三个元素
>> x(3)ans =2
(2) 取出向量中的第x个到第y的元素
>>取出向量中的第3到第5个元素
>> x(3:5)ans =2 3 4(3)取出第x个到第y个元素中,从第x个数开始,下标间隔为z的所有元素
>> %取出第二个到第十个中,从第二个数开始,间隔为2的所有数
>> x(2:2:10)ans =1 3 5 7 9(4)随便取出一些下标所对应的元素,构成一个新的向量
>> %随便取下标,举例:取出下标为10,1,8,9的元素构成的向量
>> x([10 1 8 9])ans =9 0 7 8(5)怎么把一些按顺序取的元素和不按顺序取的元素合并到一起,构成一个新的向量呢?----拼接向量元素
>> %拼接向量元素
>> [2:5 [10 1 8 9]]ans =2 3 4 5 10 1 8 9(6)如果有两个向量,怎么把两个向量中的某些元素合并到一起?
>> x=0:1:10x =0 1 2 3 4 5 6 7 8 9 10>> y=2:2:12y =2 4 6 8 10 12>> a=[x(2:5),y([6 4 1 3])]a =1 2 3 4 12 8 2 6
注意:和C语言数组的调用不同,matlab的向量元素下标是从1开始的,而不是0。
四.向量的运算
向量可以看成是一种特殊的矩阵,因此矩阵的运算对向量同样适用。除此以外,向量还是矢量运算的基础,所以还有一些特殊的运算,主要包括向量的点积、叉积和混合积。
向量的四则运算与一般数值的四则运算相同,相当于将向量中的元素拆开,分别进行加减四则运算,最后将运算结果重新组合成向量。
(1)向量的定义和赋值
>> x=logspace(0,5,6)x =列 1 至 51 10 100 1000 10000列 6100000
(2)单个向量的加减乘除法
>> x=0:2:10x =0 2 4 6 8 10>> %每一位都+x
>> x+10ans =10 12 14 16 18 20>> y=x+10y =10 12 14 16 18 20>> %每一位都-x
>> x-2ans =-2 0 2 4 6 8>> y=x-2y =-2 0 2 4 6 8>> y-xans =-2 -2 -2 -2 -2 -2>> x+yans =-2 2 6 10 14 18>> x*10ans =0 20 40 60 80 100>> x/2ans =0 1 2 3 4 5如果对每个元素进行很多运算
>> x=0:2:10x =0 2 4 6 8 10>> x+1-1+5*2ans =10 12 14 16 18 20
两个向量相加减
>> x+5-(x-1)ans =6 6 6 6 6 6(3)两个矩阵的点乘和点除
要求向量的维度一致。
>> x=0:2:10x =0 2 4 6 8 10>> y=1:2:11y =1 3 5 7 9 11>> x.*yans =0 6 20 42 72 110>> x./yans =0 0.6667 0.8000 0.8571 0.8889 0.9091>> x.*y'ans =0 2 4 6 8 100 6 12 18 24 300 10 20 30 40 500 14 28 42 56 700 18 36 54 72 900 22 44 66 88 110>> x*y'ans =250(4)向量的点积运算(求的是两个向量的数量积)
①dot(a,b)->对应两个元素相乘后,相加得到一个值
>> a=1:2:10a =1 3 5 7 9>> b=2:2:11b =2 4 6 8 10>> dot(a,b)
>> %点积
ans =190>> a.*b
>> %点乘
ans =2 12 30 56 90>> a*b'
>> %矩阵相乘
ans =190
②dot(a,b,dim)
对于向量(1 维数组):dim 只能为 1(因为只有一个维度)。
对于矩阵, dim=1 表示按列计算,dim=2 表示按行计算。
对于高维数组(如 3 维、4 维等):dim 可以是 1、2、……、直到数组的总维数。
>> a=[1,2;3,4]a =1 23 4>> b=[5,6;7,8]b =5 67 8>> dot(a,b,1)
>> % 按列计算点积:[1*5+3*7, 2*6+4*8] = [26, 44]
ans =26 44>> dot(a,b,2)
>>% 按行计算点积:[1*5+2*6; 3*7+4*8] = [17; 53]
ans =1753
(5)向量的叉积运算(求法向量)
我们知道,在空间解析几何学中,两个向量叉乘的结果是一个过两相交向量交点且垂直于两向量所在平面的向量。在MATLAB中,向量的积运算可由函数cross来实现。cross函数调用格式见表 4-3。


>> a=[1 2 3]a =1 2 3>> b=[2 3 4]b =2 3 4>> c=cross(a,b)c =-1 2 -1>> %结果验证->cross所求向量和a,b垂直
>> c=cross(a,b)c =-1 2 -1>> dot(a,c)ans =0>> dot(b,c)ans =0 (6)向量的混合积运算
(6)向量的混合积运算
>> a=[1 2 3]a =1 2 3>> b=[2 3 4]b =2 3 4>> dot(a,cross(a,b))ans =0-------------------------------------------------------
编自2025/8/2。把多项式基础学了一下, 运算里有几个不太熟悉没看懂想干啥哈哈哈,先不管了,以后用得到再说吧。
