当前位置： 首页 > news >正文

SM2椭圆曲线密码算法原理与纯C语言实现详解

news 2025/8/3 12:07:18

目录

    • 1. SM2算法概述
    • 2. SM2加密算法原理
      • 2.1 数学基础
      • 2.2 加密过程
    • 3. SM2解密算法原理
      • 3.1 解密过程
    • 4. 关键数学原理
      • 4.1 椭圆曲线点乘
      • 4.2 密钥派生函数KDF
      • 4.3 异或运算
    • 5. 安全性分析
    • 6. 实现要点
      • 6.1 内存管理
      • 6.2 坐标转换
      • 6.3 点运算验证
    • 7. 性能优化建议
    • 8.源码实现
    • 9.测试验证
    • 10. 总结

1. SM2算法概述

SM2是中国国家密码管理局发布的椭圆曲线公钥密码算法，基于椭圆曲线密码学（ECC）原理。它使用256位素数域上的椭圆曲线，具有安全性高、密钥长度短等优点。

2. SM2加密算法原理

2.1 数学基础

SM2基于椭圆曲线方程：y² = x³ + ax + b（在有限域Fp上）

核心参数：

  • 素数p：256位
  • 椭圆曲线参数a、b
  • 基点G的阶n
  • 私钥d（随机数）
  • 公钥P = dG

2.2 加密过程

int sims_sm2_encrypt(unsigned char *msg, int msglen, unsigned char *wx, int wxlen, unsigned char *wy, int wylen, unsigned char *outmsg)

加密步骤：

  1. 生成随机数k

    uint8_t fixed_k[32] = {0x4B, 0x62, 0xEE, 0xFD, ...};
str_to_bn(k, fixed_k);

  2. 计算C1 = kG

    eccpoint_mult_G_jacobian(P1, k);  // P1 = kG
bn_to_str(x1, P1);                // 提取x坐标
bn_to_str(y1, P1 + array_len);    // 提取y坐标
memcpy(C1, x1, 32);               // C1 = (x1, y1)
memcpy(C1 + 32, y1, 32);

  3. 计算C2 = kP

    eccpoint_t PB;
str_to_bn(PB, wx);                // 公钥P的x坐标
str_to_bn(PB + array_len, wy);    // 公钥P的y坐标
eccpoint_mult_jacobian(P2, PB, k); // P2 = kP
bn_to_str(x2, P2);                // 提取x2, y2
bn_to_str(y2, P2 + array_len);

  4. 密钥派生函数KDF

    kdf(x2, y2, msglen, outmsg+64);   // 从(x2,y2)派生密钥t

  5. 计算密文C2

    str_xor(C2, msg, outmsg+64, msglen); // C2 = M ⊕ t

  6. 计算哈希值C3

    memcpy(H3, x2, 32);               // H3 = x2 || M || y2
memcpy(H3 + 32, msg, msglen);
memcpy(H3 + 32 + msglen, y2, 32);
sm3(H3, msglen + 64, C3);         // C3 = SM3(H3)

  7. 组合密文

    memcpy(outmsg, C1, 64);           // 输出 = C1 || C2 || C3
memcpy(outmsg + 64, C2, msglen);
memcpy(outmsg + 64 + msglen, C3, 32);

3. SM2解密算法原理

3.1 解密过程

int sims_sm2_decrypt(unsigned char *msg, int msglen, unsigned char *privkey, int privkeylen, unsigned char *outmsg)

解密步骤：

  1. 解析密文

    memcpy(C1, msg, 64);              // 提取C1
memcpy(C2, msg + 64, msglen);     // 提取C2
memcpy(C3, msg + 64 + msglen, 32); // 提取C3

  2. 验证C1的有效性

    str_to_bn(x1, c1);                // 解析C1的x,y坐标
str_to_bn(y1, c1 + 32);
bn_set(p1, x1);
bn_set(p1 + array_len, y1);if (!is_eccpoint(p1)) return -2;  // 验证是否为有效椭圆曲线点
if (eccpoint_is_zero(p1)) return -3; // 验证是否为零点

  3. 计算dC1

    str_to_bn(d, privkey);            // 私钥d
eccpoint_mult_jacobian(p2, p1, d); // p2 = dC1
bn_to_str(x2, p2);                // 提取x2, y2
bn_to_str(y2, p2 + array_len);

  4. 密钥派生

    kdf(x2, y2, msglen, outmsg);      // 从(x2,y2)派生密钥t

  5. 恢复明文

    str_xor(outmsg, C2, outmsg, msglen); // M = C2 ⊕ t

  6. 验证哈希值

    memcpy(H3, x2, 32);               // 重新计算H3
memcpy(H3 + 32, outmsg, msglen);
memcpy(H3 + 32 + msglen, y2, 32);
sm3(H3, 64 + msglen, u);          // u = SM3(H3)if (0 != memcmp(u, C3, 32)) return -5; // 验证C3

4. 关键数学原理

4.1 椭圆曲线点乘

核心操作是椭圆曲线点乘：Q = kP

  • 加密时：C1 = kG，P2 = kP
  • 解密时：P2 = dC1 = d(kG) = k(dG) = kP

4.2 密钥派生函数KDF

KDF将椭圆曲线点的坐标转换为对称密钥：

kdf(x2, y2, msglen, t);  // 从(x2,y2)派生msglen长度的密钥t

4.3 异或运算

明文与派生密钥进行异或运算：

C2 = M ⊕ t    // 加密
M = C2 ⊕ t    // 解密

5. 安全性分析

  1. 离散对数问题：基于椭圆曲线离散对数问题的困难性
  2. 随机数k：每次加密使用不同的随机数k
  3. 哈希验证：C3用于验证密文完整性
  4. 密钥派生：KDF确保密钥的随机性和均匀分布

6. 实现要点

6.1 内存管理

uint8_t *t = malloc(sizeof(uint8_t) * msglen);
uint8_t *C1 = malloc(sizeof(uint8_t) * 64);
uint8_t *C2 = malloc(sizeof(uint8_t) * msglen);
// 使用完毕后释放
free(t); free(C1); free(C2);

6.2 坐标转换

bn_to_str(x1, P1);                // 大数转字符串
str_to_bn(PB, wx);                // 字符串转大数

6.3 点运算验证

if (!is_eccpoint(p1)) return -2;  // 验证椭圆曲线点
if (eccpoint_is_zero(p1)) return -3; // 验证非零点

7. 性能优化建议

  1. 使用雅可比坐标：eccpoint_mult_jacobian避免模逆运算
  2. 预计算：可以预计算一些常用的椭圆曲线点
  3. 并行化：KDF和哈希计算可以并行进行
  4. 内存池：避免频繁的内存分配和释放

8.源码实现

以下代码为纯c语言的实现，无任何三方库的依赖，代码量极小。方便移植到各种系统包括嵌入式单片机环境中。需要完整测试代码的可以联系博主。

/*** SM2加密算法实现* @param msg: 待加密的明文* @param msglen: 明文长度* @param wx: 公钥x坐标* @param wxlen: 公钥x坐标长度* @param wy: 公钥y坐标* @param wylen: 公钥y坐标长度* @param outmsg: 输出密文* @return: 0成功，-1失败*/
int sims_sm2_encrypt(unsigned char *msg, int msglen, unsigned char *wx, int wxlen, unsigned char *wy, int wylen, unsigned char *outmsg)
{// 验证公钥坐标长度是否为32字节if (wxlen != 32 || wylen != 32) {return -1;}// 声明变量：椭圆曲线点的坐标uint8_t x1[32];  // C1点的x坐标uint8_t y1[32];  // C1点的y坐标uint8_t x2[32];  // P2点的x坐标uint8_t y2[32];  // P2点的y坐标// 声明变量：密文组成部分uint8_t *t;      // 密钥派生函数生成的密钥uint8_t *C1;     // 密文第一部分：kGuint8_t *C2;     // 密文第二部分：明文⊕密钥uint8_t C3[32];  // 密文第三部分：哈希值// 哈希计算缓冲区，大小根据明文长度调整uint8_t H3[1028]; // 用于计算C3的哈希输入// 分配内存：密钥tif ((t = (uint8_t *)malloc(sizeof(uint8_t) * msglen)) == NULL)return -1;// 分配内存：C1（64字节：32字节x坐标 + 32字节y坐标）if ((C1 = (uint8_t *)malloc(sizeof(uint8_t) * 64)) == NULL)return -1;// 分配内存：C2（与明文等长）if ((C2 = (uint8_t *)malloc(sizeof(uint8_t) * msglen)) == NULL)return -1;printf("ok1\n");// 使用do-while(0)结构，便于错误处理和资源清理do{bn_t k;  // 大整数类型，用于存储随机数k// 使用固定的随机数k（实际应用中应该使用真随机数）uint8_t fixed_k[32] = {0x4B, 0x62, 0xEE, 0xFD, 0x6E, 0xCF, 0xC2, 0xB9, 0x5B, 0x92, 0xFD, 0x6C, 0x3D, 0x95, 0x75, 0x14, 0x8A, 0xFA, 0x17, 0x42, 0x55, 0x46, 0xD4, 0x90, 0x18, 0xE5, 0x38, 0x8D, 0x49, 0xDD, 0x7B, 0x4F};str_to_bn(k, fixed_k);  // 将字节数组转换为大整数eccpoint_t P1, P2;  // 椭圆曲线点类型// 计算C1 = kG（基点G的k倍）// 根据编译选项选择不同的点乘函数
#ifdef NIST_CURVE// 使用通用的椭圆曲线点乘函数eccpoint_mult_jacobian(P1, G, k);
#else// 使用针对SM2基点G优化的专用点乘函数eccpoint_mult_G_jacobian(P1, k);
#endif// 将P1点的坐标转换为字节数组bn_to_str(x1, P1);                    // x坐标bn_to_str(y1, P1 + array_len, y1);   // y坐标// 构造C1：将x1和y1坐标复制到C1中// 注意：这里没有添加0x04前缀（标准格式通常包含）memcpy(C1, x1, 32);      // 复制x坐标memcpy(C1 + 32, y1, 32); // 复制y坐标// 构造公钥点PB：将输入的x,y坐标转换为椭圆曲线点eccpoint_t PB;str_to_bn(PB, wx);                    // 公钥x坐标str_to_bn(PB + array_len, wy);       // 公钥y坐标// 计算P2 = kPB（公钥的k倍）eccpoint_mult_jacobian(P2, PB, k);// 将P2点的坐标转换为字节数组bn_to_str(x2, P2);                    // x坐标bn_to_str(y2, P2 + array_len);       // y坐标// 构造xy2：将P2的x,y坐标合并为64字节uint8_t xy2[64];memcpy(xy2, x2, 32);      // 复制x坐标memcpy(xy2 + 32, y2, 32); // 复制y坐标printf("ok2\n");// 使用密钥派生函数KDF从(x2,y2)生成密钥t// 生成的密钥存储在outmsg+64位置if (kdf(x2, y2, msglen, outmsg+64) == 0) {return -1;  // KDF失败}printf("ok3\n");} while (0);// 计算C2：明文与派生密钥进行异或运算str_xor(C2, msg, outmsg+64, msglen);// 构造H3用于计算C3：H3 = x2 || msg || y2memcpy(H3, x2, 32);                    // 复制x2memcpy(H3 + 32, msg, msglen);          // 复制明文memcpy(H3 + 32 + msglen, y2, 32);     // 复制y2// 计算C3：对H3进行SM3哈希运算sm3(H3, msglen + 64, C3);// 构造最终密文：C1 || C2 || C3memcpy(outmsg, C1, 64);                    // 复制C1memcpy(outmsg + 64, C2, msglen);           // 复制C2memcpy(outmsg + 64 + msglen, C3, 32);     // 复制C3// 释放分配的内存free(t);free(C1);free(C2);return 0;  // 成功
}/*** SM2解密算法实现* @param msg: 待解密的密文* @param msglen: 密文长度* @param privkey: 私钥* @param privkeylen: 私钥长度* @param outmsg: 输出明文* @return: 0成功，负数表示错误码*/
int sims_sm2_decrypt(unsigned char *msg, int msglen, unsigned char *privkey, int privkeylen, unsigned char *outmsg)
{// 验证私钥长度是否为32字节if (privkeylen != 32) {return -1;}// 验证密文长度是否足够（至少96字节：64字节C1 + 明文长度 + 32字节C3）if(msglen < 96)return 0;// 减去C1和C3的长度，得到实际明文长度msglen -= 96;// 声明变量uint8_t *t;      // 密钥派生函数生成的密钥uint8_t *C2;     // 密文第二部分uint8_t x2[32];  // 计算得到的x坐标uint8_t y2[32];  // 计算得到的y坐标uint8_t u[32];   // 重新计算的哈希值uint8_t C3[32];  // 密文第三部分（哈希值）uint8_t C1[64];  // 密文第一部分// 分配内存if ((t = (uint8_t *)malloc(sizeof(uint8_t) * msglen)) == NULL)return -1;if ((C2 = (uint8_t *)malloc(sizeof(uint8_t) * msglen)) == NULL)return -1;// 提取C1：密文的前64字节memcpy(C1, msg, 64);// 将私钥转换为大整数类型bn_t d;str_to_bn(d, privkey);// 解析C1的x,y坐标bn_t x1, y1;uint8_t *c1 = C1;str_to_bn(x1, c1);      // 提取x坐标c1 += 32;str_to_bn(y1, c1);      // 提取y坐标// 构造椭圆曲线点p1eccpoint_t p1;bn_set(p1, x1);                    // 设置x坐标bn_set(p1 + array_len, y1);       // 设置y坐标// 验证p1是否为有效的椭圆曲线点if (!is_eccpoint(p1)) {free(t);free(C2);return -2;  // 无效的椭圆曲线点}printf("ok1\n");// 验证p1是否为零点if (eccpoint_is_zero(p1)) {free(t);free(C2);return -3;  // 零点错误}printf("ok2\n");// 计算p2 = d*p1（私钥与C1的点乘）eccpoint_t p2;eccpoint_mult_jacobian(p2, p1, d);// 将p2的坐标转换为字节数组bn_to_str(x2, p2);                    // x坐标bn_to_str(y2, p2 + array_len);       // y坐标// 构造xy2：将x2,y2合并为64字节uint8_t xy2[64];uint8_t *pxy2 = xy2;memcpy(pxy2, x2, 32);      // 复制x坐标memcpy(pxy2 + 32, y2, 32); // 复制y坐标// 使用密钥派生函数KDF从(x2,y2)生成密钥tif (kdf(x2, y2, msglen, outmsg) == 0) {return -1;  // KDF失败}printf("ok3\n");printf("ok4\n");// 提取C2：密文的中间部分memcpy(C2, msg + 64, msglen);// 恢复明文：C2与派生密钥进行异或运算str_xor(outmsg, C2, outmsg, msglen);printf("ok5\n");// 打印解密结果（调试用）PrintBuf(outmsg, msglen);// 重新计算哈希值用于验证uint8_t *H3;if ((H3 = (uint8_t *)malloc(sizeof(uint8_t) * (msglen + 64))) == NULL)return -1;// 构造H3：x2 || 明文 || y2memcpy(H3, x2, 32);                    // 复制x2memcpy(H3 + 32, outmsg, msglen);       // 复制明文memcpy(H3 + 32 + msglen, y2, 32);     // 复制y2printf("ok5-1,msglen=%d\n",msglen);// 计算哈希值usm3(H3, 64 + msglen, u);printf("ok6\n");// 提取C3：密文的最后32字节memcpy(C3, msg + 64 + msglen, 32);// 验证哈希值：比较重新计算的哈希值u与C3if (0 != memcmp(u, C3, 32)) {free(t);free(C2);free(H3);return -5;  // 哈希验证失败}// 释放分配的内存free(t);free(C2);free(H3);return 0;  // 解密成功
}

9.测试验证

下面写一个main函数，对上述实现进行加解密测试：

#include <stdio.h>
#include <string.h>void PrintBuf(unsigned char *buf, int	buflen)
{int i;printf("\n");printf("len = %d\n", buflen);for(i=0; i<buflen; i++) {if (i % 32 != 31)printf("%02x", buf[i]);elseprintf("%02x\n", buf[i]);}printf("\n");return;
}void Printch(unsigned char *buf, int	buflen)
{int i;for (i = 0; i < buflen; i++) {if (i % 32 != 31)printf("%c", buf[i]);elseprintf("%c\n", buf[i]);}printf("\n");//return 0;
}extern int sims_sm2_encrypt(unsigned char *msg, int msglen, unsigned char *wx, int wxlen, unsigned char *wy, int wylen, unsigned char *outmsg);
extern int sims_sm2_decrypt(unsigned char *msg, int msglen, unsigned char *privkey, int privkeylen, unsigned char *outmsg);int sm2_test()
{printf("sm2 test 0....\n");unsigned char dB[] = { 0x13,0xd5,0xa9,0x1d,0x02,0x5a,0xe5,0xfb,0xf4,0x7b,0x10,0xa5,0xfc,0x98,0xb9,0x13,0x49,0x4d,0xf6,0x6a,0x6f,0xeb,0x1c,0xf8,0xa7,0x26,0x81,0xee,0xf6,0xc3,0x3d,0xed };unsigned char xB[] = { 0xf7,0x9e,0x06,0x71,0xb8,0xe3,0xbc,0x54,0x2a,0xab,0x81,0xcf,0xa1,0xd1,0xa6,0xc1,0x58,0xb9,0xbd,0xca,0xad,0x46,0x4b,0xbf,0x9e,0x8a,0x79,0x6f,0x8e,0xc9,0x2e,0x27 };unsigned char yB[] = {0xb2,0x2f,0x1f,0x3d,0x72,0xad,0x1e,0x99,0x23,0x51,0xf7,0xce,0xcf,0xdc,0xd5,0x03,0xaa,0x6d,0xf9,0x3b,0xef,0xdd,0xb8,0xdd,0x92,0x14,0x7e,0x74,0x57,0xdf,0x4d,0x44 };unsigned char tx[256]={0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31,0x31};unsigned char etx[256];unsigned char mtx[256];unsigned char hexOut[256] = {0x52,0xB4,0x38,0xC6,0xAB,0xF7,0x68,0x27,0x13,0x7C,0x55,0x9D,0xEF,0x13,0xC0,0xE0,0x09,0x45,0x29,0x44,0x7C,0xFC,0xBD,0x6E,0xFB,0x42,0x66,0x73,0xF2,0x7B,0xCF,0x2B,0x29,0xBF,0x1A,0x67,0xBB,0x8B,0x19,0x53,0x12,0x5C,0x13,0x9B,0x52,0xB8,0x81,0x0F,0x20,0xCC,0x16,0xEA,0x42,0x1B,0x44,0xD0,0x10,0xBF,0x42,0xF2,0x3B,0x95,0xE8,0xB7,0x52,0x5E,0x77,0xC7,0xE4,0xBD,0x40,0xFC,0xA5,0xA6,0xD4,0x87,0x83,0xBD,0xFB,0x19,0x91,0x9A,0x0A,0x3C,0x7B,0x2F,0x87,0x0A,0xAD,0x74,0x13,0xBC,0x94,0x3F,0x84,0x50,0x4B,0x7B,0x9A,0x1F,0x7C,0xFE,0x7E,0xBC,0x46,0xCB,0x90,0x98,0x15,0x22,0x82,0x23,0x30,0x10,0x96,0xB8,0x65,0xFC,0x97,0x4C,0x92,0xB1,0x07,0x54,0x4D,0xB0,0xFB,0x91,0xD5,0xEB,0x5A,0x07,0xFC,0x48,0x2F,0x14,0x91,0xFC,0x2D,0x3A,0x6C,0x50,0x01,0xB9,0x7E,0x1C,0xE7,0x40,0x6A,0x21,0x0F,0x9A,0x62,0xE7,0xC3,0x0B,0xB4,0x7A,0xAD,0x93,0x04,0x35,0x5F,0x87,0xA0,0xDD,0x70,0x22,0x5F,0x65,0xB1,0x95,0x31,0xC3,0x3E,0xA8,0xEF,0xE1,0x74,0x4D,0x16,0x5A,0x6F,0x07,0xB2,0x72,0x38,0xEA,0x2A,0xFD,0x28,0xD8,0xCF,0x5E,0x1A,0x15,0x4A,0xA0,0x1F,0x87,0x2B,0xE8,0xA0,0xED,0xED,0xAD,0xB6,0x14,0xA4,0x83,0x16,0x0A,0xAB,0xAA,0x43,0xF2,0x2E,0xDB,0xE6,0x95,0x23,0xC9,0xF4,0x4F,0xEC,0x94,0x7C,0x32,0x7A,0x6C,0x95,0x5A,0x33,0x8B,0xCB,0x7B,0x05,0xD3,0x5B,0x54,0x9C,0x4F,0xAC,0x9D,0x14,0xA3,0x51,0xA5,0xEB,0x91};//FILE *fp=0;int wxlen, wylen, privkeylen,len;//fopen(&fp, "5.txt", "r");//len=fread_s(tx, 256,sizeof(unsigned char), 256, fp);//fp = fopen("5.txt","r");//len=fread(tx,1,256,fp);memset(tx,0x31,154);len = 154;tx[len] = 0;PrintBuf(tx, len);//sm2_keygen(xB, &wxlen, yB, &wylen, dB, &privkeylen);printf("dB: ");PrintBuf(dB, 32);printf("xB: ");PrintBuf(xB, 32);printf("yB: ");PrintBuf(yB, 32);// mode =1,ΪC1C3C2ģʽ�� 0ΪC1C2C3ģʽsims_sm2_encrypt(tx,len,xB,32,yB,32,etx);printf("\n``````````````````this is encrypt```````````````````\n");PrintBuf(etx, 64 +len + 32);printf("\n``````````````````this is decrypt```````````````````\n");//sm2_decrypt(etx,64+len+32,dB,32,mtx);//int ret = sims_sm2_decrypt(etx,64+len+32,dB,32,mtx);if( ret < 0){printf("sm2_decrypt errors!,code=%d\n",ret);}else{PrintBuf(mtx, len);Printch(mtx, len);}printf("\n``````````````````this is end```````````````````````\n");return 0;
}int main(){sm2_test();return 0;
}

测试结果如下图所示：
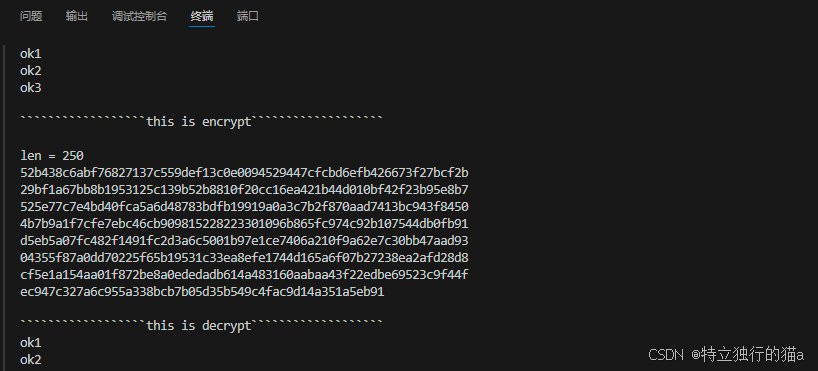
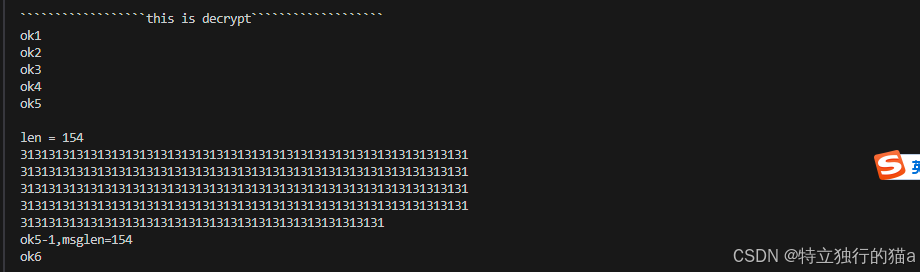
在这里插入图片描述
在这里插入图片描述
分别在x86和x64及stm32单片机上进行测试，测试结果符合正确。且占用资源极低。

10. 总结

SM2算法通过椭圆曲线密码学提供了高安全性的公钥加密方案。其核心在于：

  • 加密：使用随机数k和公钥P生成密文C1、C2、C3
  • 解密：使用私钥d从C1恢复出相同的中间值，进而恢复明文
  • 验证：通过哈希值C3确保密文完整性

纯C语言实现需要处理大数运算、椭圆曲线点运算、密钥派生等复杂操作，但通过模块化设计可以构建出高效、安全的SM2加解密系统。

http://www.dtcms.com/a/312002.html

相关文章：

  • #Linux内存管理# 用一个案例详细介绍ARMv7-A架构 缺页中断处理的原理
  • ARMv8/v9架构FAR_EL3寄存器介绍
  • imx6ull-驱动开发篇6——Linux 设备树语法
  • P10816 [EC Final 2020] Namomo Subsequence|普及+
  • 堆----1.数组中的第K个最大元素
  • [buuctf-misc]喵喵喵
  • Linux学习--数据结构
  • 前端-移动Web-day3
  • 基于springboot的郑州旅游景点推荐系统
  • Kotlin单例模式懒汉模式：LazyThreadSafetyMode.SYNCHRONIZED（2）
  • 多线程(二) ~ 线程核心属性与状态
  • C#中对于List的多种排序方式
  • LeeCode 88. 合并两个有序数组
  • DeepSpeed - 超大LLM分布式训练框架 ZeRO技术
  • Python day32
  • 力扣 二叉树遍历 中序/前序/后序（递归和迭代版）
  • dbt中多源数据的处理
  • 混合嵌入与置信度增强：新一代RAG技术如何提升LLM性能
  • 1.6 vue 监听
  • JavaScript 原始值与引用值
  • SQL语言学习（group by,having）
  • PyTorch 中 Tensor 统计学函数及相关概念
  • 基于单片机一氧化碳CO检测/煤气防中毒检测报警系统
  • OneCode 3.0智能分页拦截器深度解析：从拦截机制到性能优化
  • 轨道追逃博弈仿真
  • 输电线路建模与电力负荷特性详解（含等值模型与曲线分析）
  • Vue 详情模块 4
  • SQL语言学习（JOIN）
  • Orange的运维学习日记--25.Linux文件系统基本管理
  • 使用xshell连接远程腾讯云服务器，报错:Xshell Socket error Event: 32 Error: 10053