牛客——取数游戏2

题目链接：牛客--取数游戏2

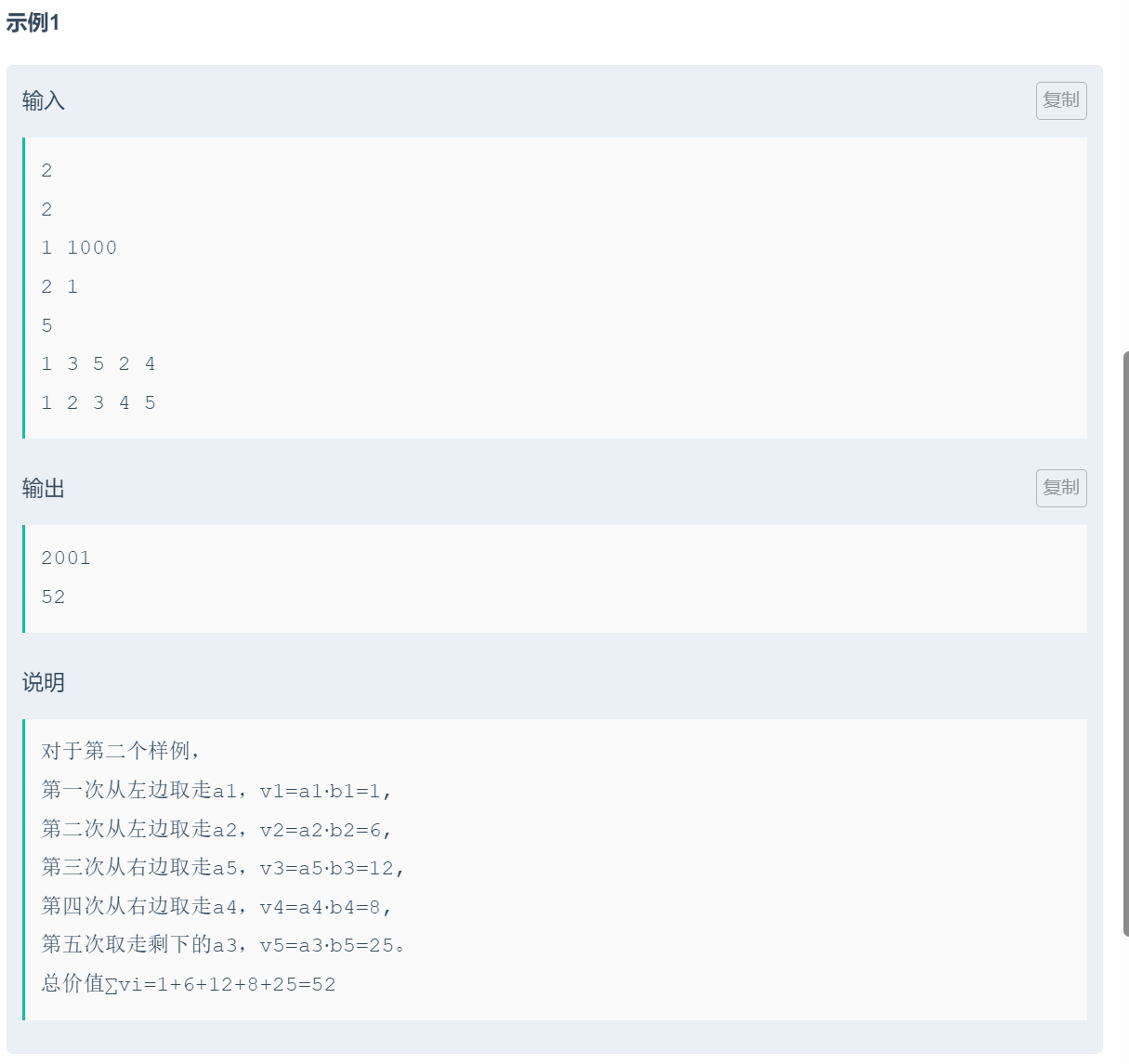
题目解答区基本都是直接写的dp代码，但对我个人而言还是好难理解，所以凭从左程云老师那里学来的经验，我决定从递归入手。

分析题目，从B数组依次向后取，每次可选择A数组最左或最右，那么我们只需要知道两种情况的最大值，即可。注意每次选A数组数字后，A数组区间会减小，我们可以基于此构建递归函数。

#include <iostream>
#include <vector>
using namespace std;
vector<int> numsA(1001);
vector<int> numsB(1001);
int func(int i, int j, int k, int n);
int main(){int t;cin >> t;while(t--){int n;cin >> n;for(int i = 0; i < n; i++){cin >> numsA[i];}for(int i = 0; i < n; i++){cin >> numsB[i];}cout << func(0, n - 1, 0, n) << endl;}
}// i表示A数组左边界 j表示A数组右边界
// k表示B数组中所要使用的数字下标
// n表示数组大小
int func(int i, int j, int k, int n){if(k == n - 1){return numsB[k] * numsA[i];}// 选数组左边int res1 = numsB[k] * numsA[i] + func(i + 1, j, k + 1, n);// 选数组右边int res2 = numsB[k] * numsA[j] + func(i, j - 1, k + 1, n);int ans = max(res1, res2);return ans;
}

在此基础上进行记忆化搜索优化。

#include <bits/stdc++.h>
using namespace std;
vector<int> numsA(1001);
vector<int> numsB(1001);
int dp[1001][1001][1001];
int func(int i, int j, int k, int n);
int main(){int t;cin >> t;while(t--){memset(dp, -1, sizeof(dp));int n;cin >> n;for(int i = 0; i < n; i++){cin >> numsA[i];}for(int i = 0; i < n; i++){cin >> numsB[i];}cout << func(0, n - 1, 0, n) << endl;}
}// i表示A数组左边界 j表示A数组右边界
// k表示B数组中所要使用的数字下标
// n表示数组大小
int func(int i, int j, int k, int n){if(dp[i][j][k] != -1){return dp[i][j][k];}if(k == n - 1){return numsB[k] * numsA[i];}// 选数组左边int res1 = numsB[k] * numsA[i] + func(i + 1, j, k + 1, n);// 选数组右边int res2 = numsB[k] * numsA[j] + func(i, j - 1, k + 1, n);int ans = max(res1, res2);dp[i][j][k] = ans;return ans;
}

但是这样使用三维数组会内存超限。考虑到 k 值是随区间大小变化的，即每当A数组区间减小1，k则增大1，所以对于递归函数，k可以由 i 和 j 直接得到，即 k = n - (j - i + 1)。优化后代码如下。

#include <bits/stdc++.h>
using namespace std;
vector<int> numsA(1001);
vector<int> numsB(1001);
int dp[1001][1001];
int func(int i, int j, int n);
int main(){int t;cin >> t;while(t--){memset(dp, -1, sizeof(dp));int n;cin >> n;for(int i = 0; i < n; i++){cin >> numsA[i];}for(int i = 0; i < n; i++){cin >> numsB[i];}cout << func(0, n - 1, n) << endl;}
}// i表示A数组左边界 j表示A数组右边界
// k表示B数组中所要使用的数字下标
// n表示数组大小
int func(int i, int j, int n){if(dp[i][j] != -1){return dp[i][j];}int k = n - (j - i + 1);if(k == n - 1){return numsB[k] * numsA[i];}// 选数组左边int res1 = numsB[k] * numsA[i] + func(i + 1, j, n);// 选数组右边int res2 = numsB[k] * numsA[j] + func(i, j - 1, n);int ans = max(res1, res2);dp[i][j] = ans;return ans;
}

到这里其实就已经AC了，不过，学习算法当然不能止步于此，试着将递归改为迭代。

将二维数组视为表（i 作为列，j 作为行），发现递归边界为对角线，空位由上方和右方决定，根据经验，从右下向左遍历即可，最终 dp[0][n - 1] 即为答案。其实想到这里后，再去回看评论区题解，那些代码就没那么晦涩难懂了。最后代码如下：

#include <bits/stdc++.h>
using namespace std;
vector<int> numsA(1001);
vector<int> numsB(1001);
int dp[1001][1001];
int func(int i, int j, int n);
int main(){int t;cin >> t;while(t--){memset(dp, -1, sizeof(dp));int n;cin >> n;for(int i = 0; i < n; i++){cin >> numsA[i];}for(int i = 0; i < n; i++){cin >> numsB[i];}//cout << func(0, n - 1, n) << endl;// 以 j 为行, i 为列构建dp表用于动态规划// 初始化对角线// k = n - (j - i + 1);for(int i = 0; i < n; ++i){// i = jdp[i][i] = numsA[i] * numsB[n - 1];}for(int i = n - 2; i >= 0; --i){for(int j = i + 1; j < n; ++j){int k = n - (j - i + 1);int res1 = numsB[k] * numsA[i] + dp[i + 1][j];    // 选左边int res2 = numsB[k] * numsA[j] + dp[i][j - 1];    // 选右边dp[i][j] = max(res1, res2);}}cout << dp[0][n - 1] << endl;}
}// i表示A数组左边界 j表示A数组右边界
// k表示B数组中所要使用的数字下标
// n表示数组大小
int func(int i, int j, int n){if(dp[i][j] != -1){return dp[i][j];}int k = n - (j - i + 1);if(k == n - 1){return numsB[k] * numsA[i];}// 选数组左边int res1 = numsB[k] * numsA[i] + func(i + 1, j, n);// 选数组右边int res2 = numsB[k] * numsA[j] + func(i, j - 1, n);int ans = max(res1, res2);dp[i][j] = ans;return ans;
}