【[CSP-J 2022] 上升点列】
题目
[CSP-J 2022] 上升点列
题目描述
在一个二维平面内,给定 n 个整数点 (x i ,y i ),此外你还可以自由添加 k 个整数点。
你在自由添加 k 个点后,还需要从 n+k 个点中选出若干个整数点并组成一个序列,使得序列中任意相邻两点间的欧几里得距离恰好为 1 而且横坐标、纵坐标值均单调不减,即 x i+1 −x i =1,y i+1 =y i 或 y i+1 −y i =1,x i+1 =x i 。请给出满足条件的序列的最大长度。
输入格式
第一行两个正整数 n,k 分别表示给定的整点个数、可自由添加的整点个数。接下来 n 行,第 i 行两个正整数 x i ,y i 表示给定的第 i 个点的横纵坐标。
输出格式
输出一个整数表示满足要求的序列的最大长度。
输入输出样例
输入 #1
8 2
3 1
3 2
3 3
3 6
1 2
2 2
5 5
5 3
输出 #1
8
输入 #2
4 100
10 10
15 25
20 20
30 30
输出 #2
103
思路
1.各点按x、y排序
2.状态:到达各点的最多序列
3.状态转移:到达该点的最多序列=前面所有点中的最多序列
4.转移方程:f[i][n]=max(f[i][n],f[j][k-dis(i,j)]+dis(i,j)+1)
f[当前点][借的点数]=max(f[当前点][借的点数],
f[当前点前的每个点][当前借的点数-i到j两点间需要的点数]
+
i到j两点间需要的点数
+
i点本身
)
5.三层循环
一层,遍历每个点(i)
二层,遍历i前所有点(j)
三层,遍历能借的点数0到k-dis(i,j)
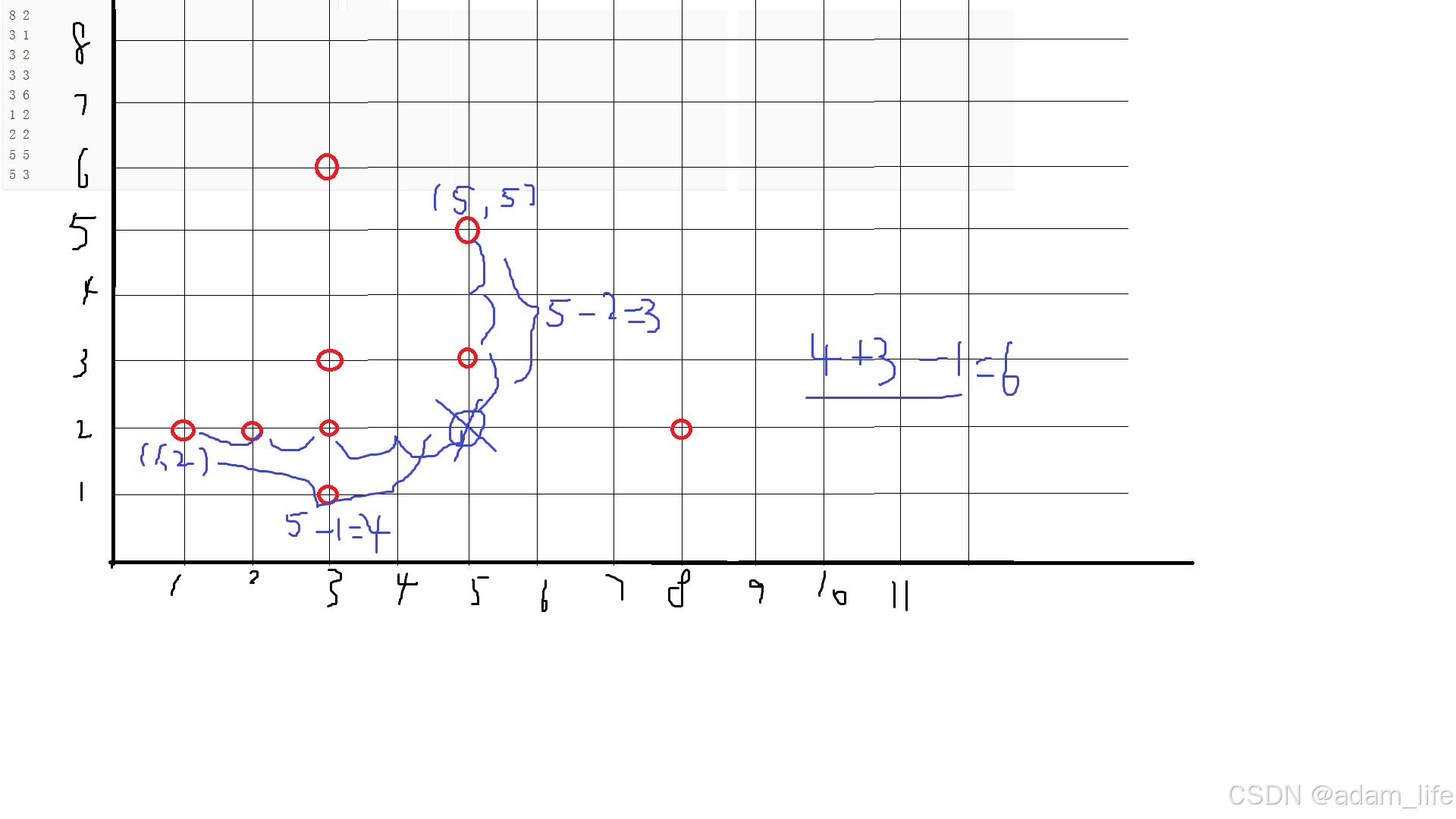
图解
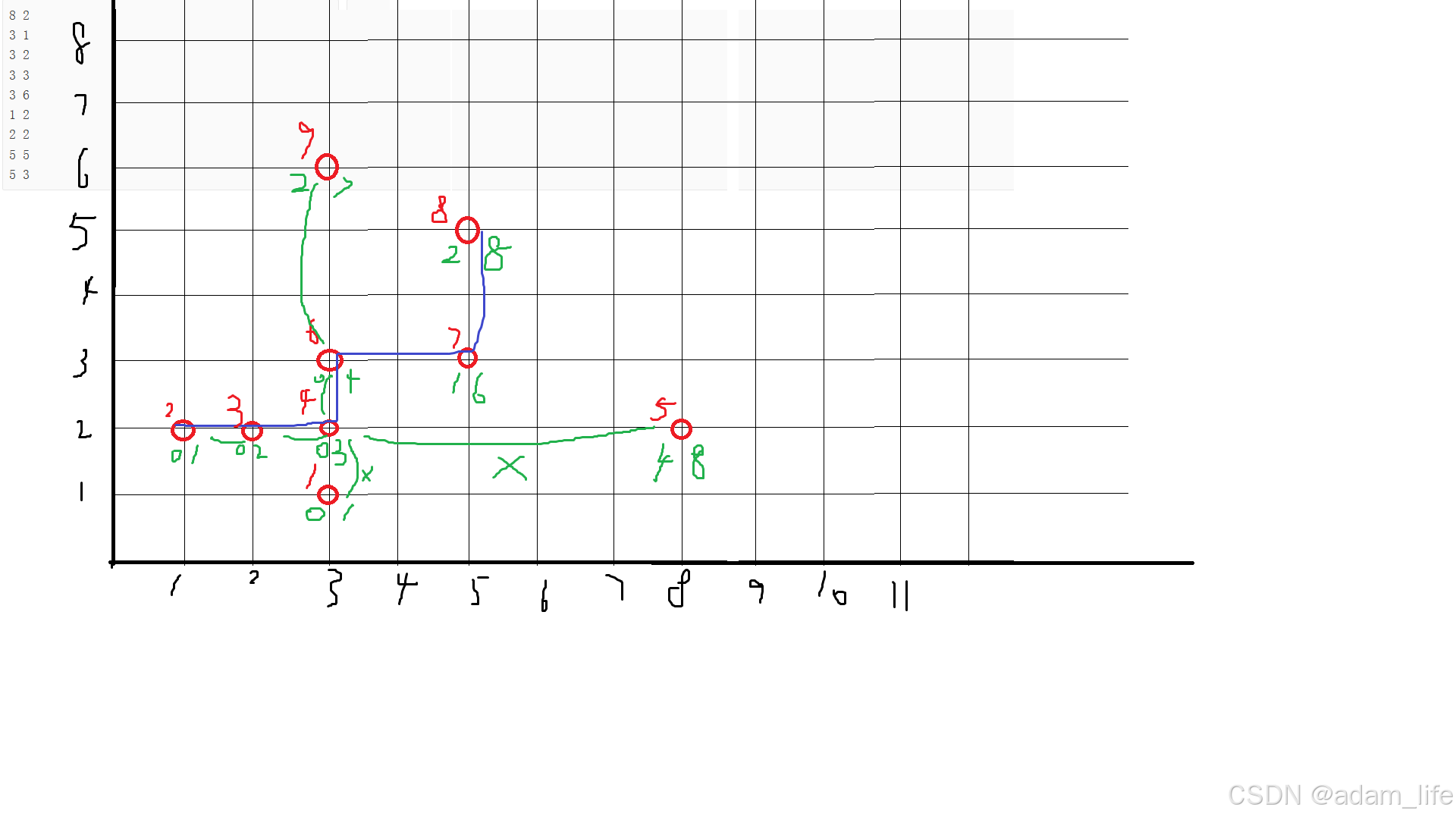
两点间欧几里得距离
代码
#include <bits/stdc++.h>
using namespace std;
int n,//整数点数 k,//可添加整数点数 x,y,//整数点的坐标 ans,//最多序列 f[501][101];//在借得不同数点情况下到达每个点的最多序列数 //f[i][x]=max(f[i][x],f[j][x-dis(i,j)]+dis(i,j)+1)
struct point{int x,y;bool operator<(const point p2)const{if(x==p2.x)return y<p2.y;return x<p2.x;}
}p[501];
int dis(int i2,int i1){return p[i1].x-p[i2].x+p[i1].y-p[i2].y-1;
}
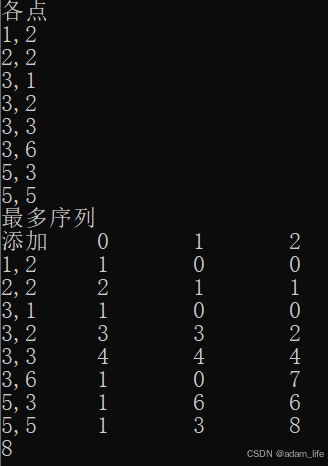
void view(){cout<<"各点"<<endl;for(int i=0;i<n;i++)cout<<p[i].x<<","<<p[i].y<<endl;
}
void view2(){cout<<"最多序列"<<endl;cout<<"添加\t";for(int x=0;x<=k;x++)cout<<x<<'\t';cout<<endl; for(int i=0;i<n;i++){cout<<p[i].x<<","<<p[i].y<<"\t";for(int x=0;x<=k;x++)cout<<f[i][x]<<'\t';cout<<endl; }}
int main(){freopen("point.in","r",stdin);cin>>n>>k;for(int i=0;i<n;i++){cin>>x>>y;p[i]=point{x,y}; }//view();sort(p,p+n);view();for(int i=0;i<n;i++){//遍历所有点 f[i][0]=1;//初始化,每个点序列起码有1 for(int j=0;j<i;j++)//遍历前面的所有点 if(p[j].y<=p[i].y){//如果是升序(右上) int m=dis(j,i);//欧几里得距离 for(int x=0;x+m<=k;x++)//j已经加的点+现在i到j加的点不超过k f[i][x+m]=max(f[i][x+m],f[j][x]+dis(j,i)+1);/*第i点用了x+m个点后的最多序列=以下中最大本来的最多序列i前j点用了x个点后的最多序列,加上i到j需要的点,+i点本身 */ } }view2();for(int i=0;i<n;i++)//遍历所有点,不一定是最后一个序列最多 for(int j=0;j<=k;j++)//用添加点最少而序列最多的 ans=max(ans,f[i][j]+k-j);//在必须用的点基础上还可以用k剩余的点 cout<<ans;return 0;
}
数据