python逻辑回归:数学原理到实战应用
一、逻辑回归简介
逻辑回归(Logistic Regression)是一种广泛应用于分类问题的机器学习算法,尽管名称中带有 “回归” 二字,但它本质上是一种强大的分类模型。
1.核心思想:
逻辑回归的核心思想是通过构建一个线性函数,结合 Sigmoid 激活函数,将特征与类别概率关联起来。其工作流程大致分为几步:首先计算输入特征的线性组合,得到一个连续值;然后将这个值传入 Sigmoid 函数,将其映射到 0 到 1 之间,得到样本属于某一类别的概率;最后根据概率值与设定阈值(通常为 0.5)的比较,确定样本的类别。
2.sigmoid函数的作用:
Sigmoid 函数凭借其独特的数学特性,在多个领域都有着广泛而重要的应用,成为连接线性与非线性、连续与离散的关键工具。
在机器学习领域,Sigmoid 函数是逻辑回归算法的核心组成部分。逻辑回归作为经典的分类算法,正是通过 Sigmoid 函数将线性回归的输出值映射到 0 到 1 之间,从而得到样本属于某一类别的概率,为分类决策提供依据。例如在垃圾邮件识别中,它能将邮件特征的线性组合结果转换为 “是垃圾邮件” 的概率,帮助系统做出判断。
深度学习领域也离不开 Sigmoid 函数的身影。在早期的神经网络中,它常被用作激活函数,为网络引入非线性因素,使神经网络能够拟合复杂的非线性关系。虽然如今在深层网络中它的地位被 ReLU 等函数部分取代,但在一些特定场景,如生成对抗网络的生成器输出层,以及需要将输出限制在 0 到 1 范围内的任务中,Sigmoid 函数仍发挥着重要作用。
在生物学研究中,Sigmoid 函数能够很好地模拟某些生物生长过程。许多生物的生长曲线都呈现出 “S” 形,初期生长缓慢,接着进入快速增长期,最后生长速度逐渐减缓并趋于稳定,这与 Sigmoid 函数的曲线特征高度吻合,因此它被用来建立生物生长模型,描述种群数量随时间的变化规律。
除此之外还有许多作用。
二、逻辑回归的数学原理
上面说明了,逻辑回归的核心思想是:通过构建一个线性函数,结合 Sigmoid 激活函数,将特征与类别概率关联起来。
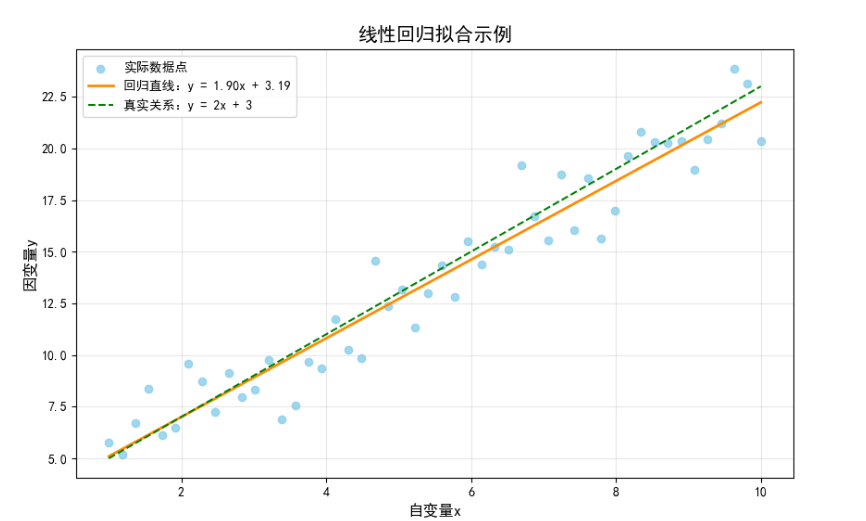
1.线性回归
定义:在N维空间中找一个像直线方程一样的函数来拟合数据而已。
z=w1x1+w2x2+⋯+wnxn+b
以一元数据为例:
2.损失函数:
损失函数的核心作用:
目标:找到一条直线(或超平面),使所有数据点的预测值与真实值的总误差最小。
线性回归最常用的损失函数是均方误差(Mean Squared Error, MSE):
公式如下:
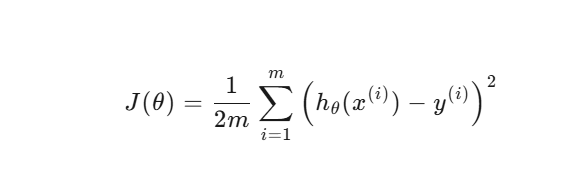
符号说明
m:样本数量(数据点个数)。
x(i):第 i 个样本的特征(自变量)。
y(i):第 i 个样本的真实值(因变量)。
hθ(x(i)):模型的预测值,即 θTx(i)。
θ:模型参数(权重和偏置)。
目标:使损失函数值最小,可以使用最小二乘法和梯度下降法实现。
3.sigmoid函数
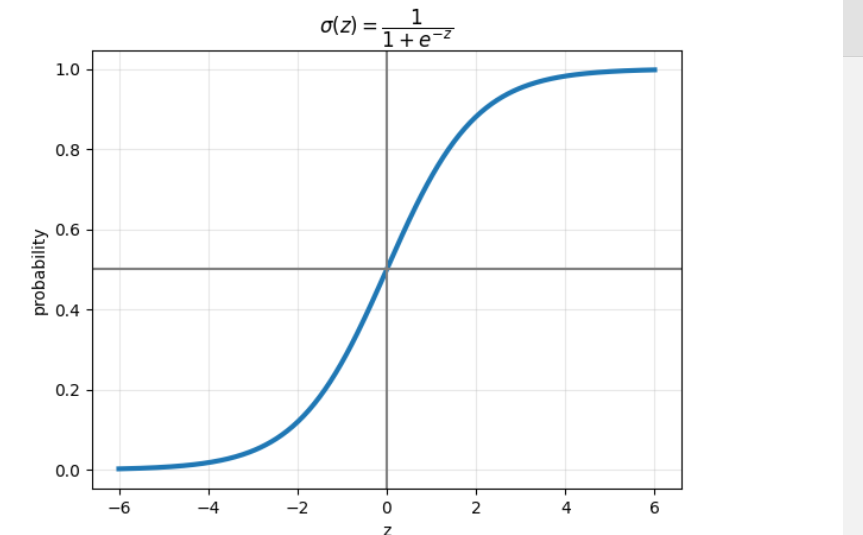
用 Sigmoid 函数把 z 映射到 0~1:
sigmoid函数公式:
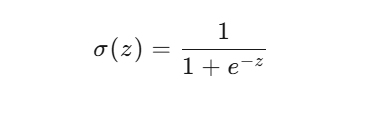
把线性函数的z带入sigmo函数:
当 z→+∞,概率接近 1
当 z→−∞,概率接近 0
当 z=0,概率 = 0.5
将数据分为0,1两类。
逻辑回归实操
1.导入数据:
使用numpy导入数据:
import numpy as np
data = np.loadtxt(r"D:\pythonProject11\class\datingTestSet2.txt")
2.提取数据:
x = data[:,:-1]
y = data[:,-1]
x = data[:,:-1]:除了最后一列的数据都提取出来
y = data[:,-1]:提取最后一列数据
3 训练集 / 测试集拆分:
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.2, random_state=1000)
- split 表示将代码切分
test_size=0.2:80 % 数据拿去训练,20 % 留给考试。
random_state=1000:固定随机种子,保证每次运行得到同样的拆分(可复现实验)。
4.训练逻辑回归:
lr = LogisticRegression(C=0.01)
lr.fit(x_train, y_train)
这里用了 ** multinomial logistic regression **(多分类逻辑回归)。
C=0.01:正则化系数越小,模型越“保守”,防止过拟合。
5.查看模型参数:
a = lr.coef_ # 形状 (3, 3),每行对应一个类别的一堆权重
b = lr.intercept_ # 形状 (3,),每个类别一个偏置
6.预测评估:
c = lr.predict(x_test) # 对测试集做预测
score = lr.score(x_test, y_test) # 平均准确率
print(c)
print("模型的正确率为:", score)
综合代码:
import numpy as np
from sklearn.linear_model import LogisticRegression
data = np.loadtxt(r"D:\pythonProject11\class\datingTestSet2.txt")x = data[:,:-1]
y = data[:,-1]
from sklearn.model_selection import train_test_split #拆分数据,一部分训练一部分测试
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=1000)
lr = LogisticRegression(C=0.01)
lr.fit(x_train,y_train)
a = lr.coef_
b = lr.intercept_
c = lr.predict(x_test)
score = lr.score(x_test,y_test)
print(c)
print("模型的正确率为:",score)
项目2:
银行贷款,读取信用卡信息,看看谁是老赖。
与上述不同的是,读取的信息需要进行脱敏化处理
为什么要做“信息脱敏”?:
护隐私:防止姓名、住址、身份证号等被直接识别。
合规要求:《个人信息保护法》《数据安全法》都明确要求“最小可用、最小暴露”。
降低风险:一旦出现数据泄露,脱敏后的信息也难以被恶意利用。
常见的数据处理:
0-1标准化
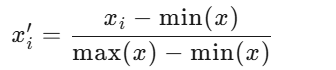
也叫离差标准化,是对原始数据的线性变换,使结果映射到[0,1]区间。
z标准化
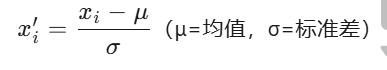
基于数据的均值和标准差进行数据的标准化。将A的原始x使用z-score标准化到x。
本次我们就会使用z标准化:
代码如下:
对Aount数据列进行z标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
2.丢弃冗余数据:
data = data.drop(['Time'], axis=1)Time:秒级时间戳,对欺诈检测意义不大,直接丢掉。
其他部分与上述项目差别不大,完整代码如下:
import pandas as pd
from sklearn.linear_model import LogisticRegressiondata = pd.read_csv("creditcard.csv")
from sklearn.preprocessing import StandardScaler #z标准化
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
data = data.drop(['Time'],axis=1)
x = data.drop("Class",axis=1)
y = data.Class
lr = LogisticRegression()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=1000)
lr.fit(x_train,y_train)
y_predict=lr.predict(x_test)
score = lr.score(x_test,y_test)from sklearn import metrics
print(metrics.classification_report(y_test,y_predict)) #把模型在测试集上的预测结果 y_predict 与真实标签 y_test 做一次“体检”,打印一份一目了然的诊断报告。运行结果如下:
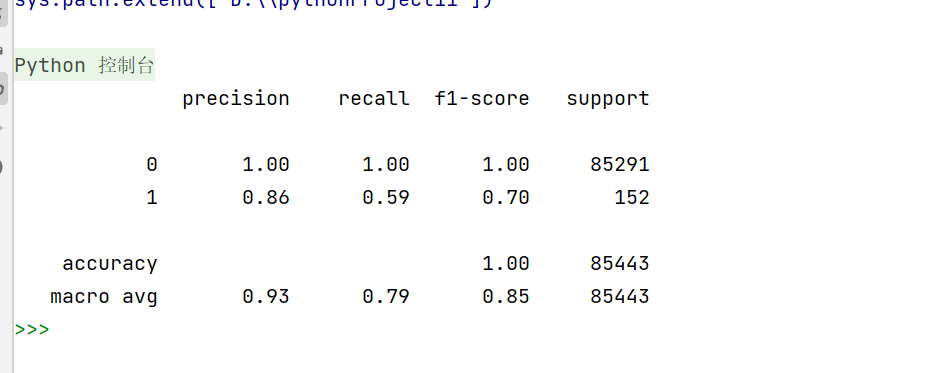
总结:逻辑回归的数学本质
逻辑回归的数学原理可以概括为:用 Sigmoid 函数将线性模型的输出映射为类别概率,通过最小化交叉熵损失函数学习最优参数,最终实现对类别的预测。
这种算法兼具线性模型的简洁性和概率模型的可解释性,虽然简单但在实际业务中(如信用评分、欺诈检测、用户流失预测等)仍被广泛使用。理解其数学原理,不仅能帮助我们更好地调参和优化模型,也能为学习更复杂的算法(如神经网络)打下基础 —— 神经网络的输出层其实就是逻辑回归的扩展。
