当前位置：首页 > news >正文

大模型的开发应用（二十）：AIGC原理

news 2025/8/2 13:32:37

这里写目录标题

0 前言
1 文生图
- 1.1 最简单的图像生成模型
- 1.2 DALL·E 2
2 Stable Diffusion
- 2.1 核心模块组成
- 2.2 文生图工作流程详解
- 2.3 图生图工作流程详解
- 2.4 不同的采样方式区别
- - ⚙️ 一、采样方法的数学本质
  - 🔬 二、主流采样方法分类与公式解析
  - - 📊 1. 基础确定性采样器（收敛型，没有随机噪声）
    - 🎲 2. 随机性采样器（不收敛型）
    - ⚡ 3. 高效多步采样器（平衡型）
    - ⚠️ 4. 淘汰或不推荐采样器
  - 📊 三、关键参数对采样效果的影响
  - 💎 四、总结：选择建议与典型场景
- 2.5 与 DALL·E 2 的结构对比
- 2.6 设计优势与局限
- 2.7 关于 Stable Diffusion 本地部署
- 2.7 总结

0 前言

上篇文章，我们介绍了AIGC的先修知识，介绍了 ViT、CLIP、VAE 和 Diffusion，这篇文章是在这些个模型的基础上，介绍图像生成模型（包括文生图和图生图），本文将重点介绍 Stable Diffusion 的原理。

1 文生图

1.1 最简单的图像生成模型

VAE 的解码器具有图像生成的功能，但是它需要一个潜空间（Latent Space）向量，如果这个向量能体现输入的文本特征，那么就可以根据这个向量生成图像。此时我们很容易想到文本特征提取器，例如最基础的 Bert，不过这里用 CLIP 中的文本编码器比较合适，因为它提取的特征和图像特征对齐了，也就是说，CLIP 的文本编码器输出的文本特征，可以认为是某张图像的特征，只不过这张图象暂时还没有，需要我们生成。

好的，现在我们可以搭建最简单的文生图模型了，架构如下图所示：
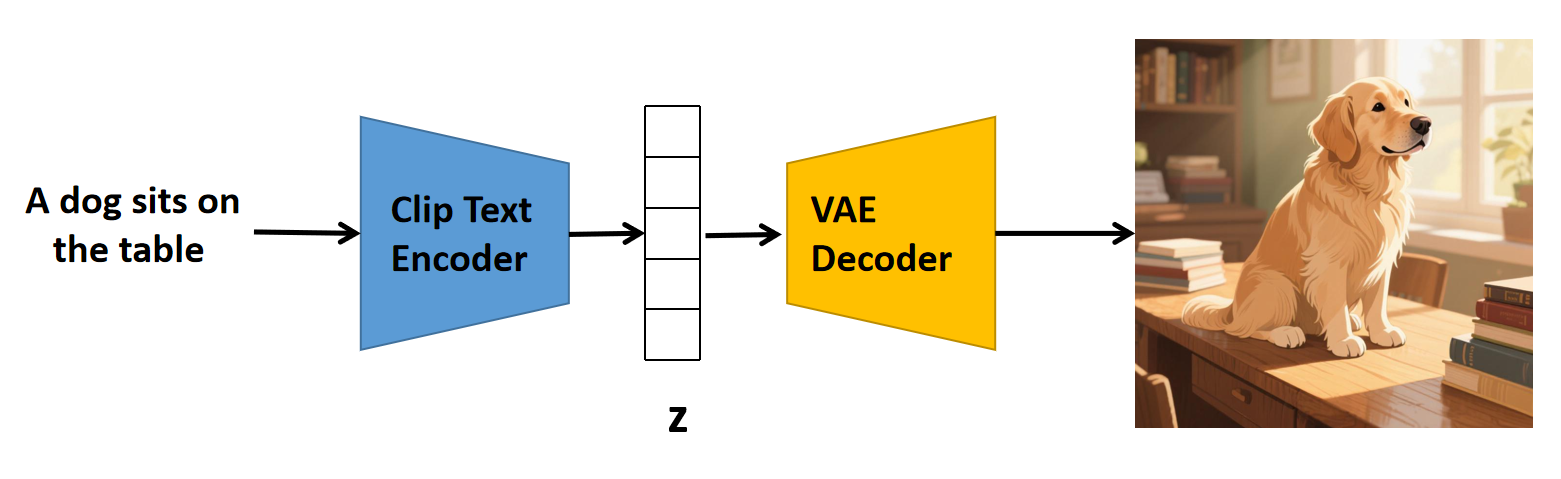
在这里插入图片描述

上面的理论模型还是有点问题的，因为 CLIP 的文本编码器输出的特征向量，它并不是某张图片的特征向量，只是两个向量在相同的分量上能同时取得最大值。这个架构只是为了方便理解后续模型用的，没有人真的这么用（或许有，只是我不知道而已），当然，也有可能经过一定的训练后，CLIP的文本编码器也能输出相关图像的特征。

1.2 DALL·E 2

CLIP 的文本编码器与图像编码器，输出的特征向量长度是相同的，并且两者强相关，那么是否可以增加一个转换模型，把文本特征向量转换成图像特征向量？DALL·E 2 模型就是这个 idea 的具体实现。

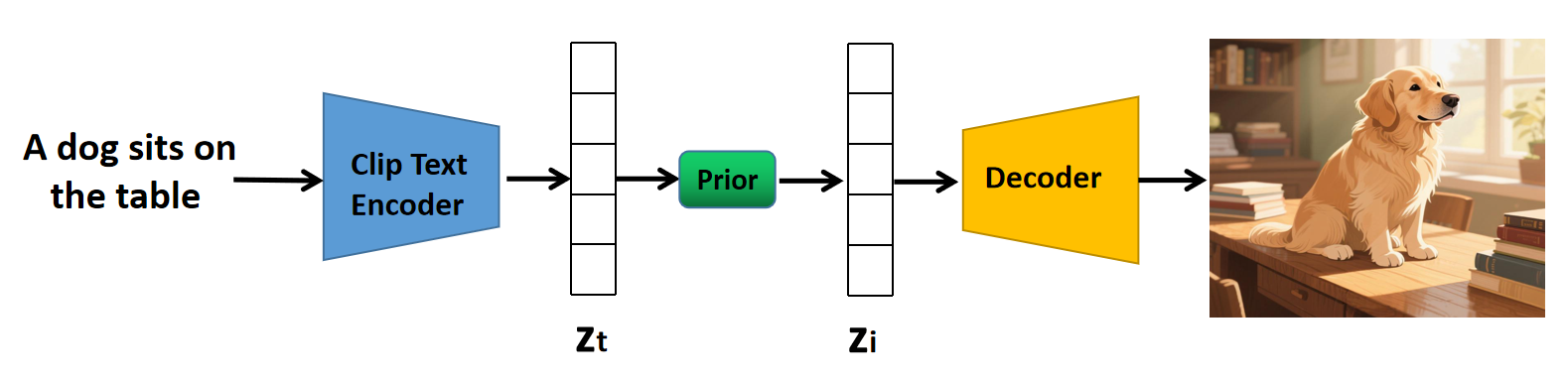
在这里插入图片描述

图中， $Z_t$ 是从文本中提取的特征，将其输入到 Prior 模块（也称为先验模块）后，得到 $Z_i$ ，它是文本所对应的图像的特征（只是这张图像未必存在），也就是说，起转换作用的是这个先验模块。

Prior 模块也是通过扩散模型实现的，以随机高斯噪声为起点，用文本特征 $Z_t$ 作为条件引导去噪方向，最后得到对应的图像特征。训练的时候，需要把 “文本-图像” 对输入到 CLIP，得到文本特征和图像特征，然后按照训练扩散模型的方式进行训练。这里不做具体展开，只需要知道 Prior 是干什么用的就行了。

训练完 Prior 后，还需要训练 Decoder。训练时使用 CLIP 的图像特征提取器，输入原始图像得到特征，然后将特征输入到 Decoder 得到生成图，计算生成图与原始图的损失函数，进而更新 Decoder 中的参数，训练时同样是冻结 CLIP 的参数。

注意，DALL·E 2 模型的 Decoder，不是 VAE 的 Decoder，而是基于扩散模型的解码器，因为 DALL·E 2 模型并非我们要掌握的重点，所以只需要知道 DALL·E 2 模型的 Decoder 与 VAE 的 Decoder 完成了相同的功能就行。

2 Stable Diffusion

Stable Diffusion（SD）是一种基于潜在扩散模型（Latent Diffusion Model, LDM） 的文本到图像生成架构，其核心设计通过将高维像素空间压缩到低维潜空间，显著降低了计算复杂度。以下是其详细结构及工作流程：

2.1 核心模块组成

Stable Diffusion 包含三个核心模块，协同完成从文本到图像的生成过程：

CLIP 文本编码器（Text Encoder）
- 功能：将输入的自然语言描述（Prompt）转换为语义向量（Text Embedding）。
- 实现：使用预训练的 CLIP 模型的文本编码部分，输出维度为 [B, K, E]（B为批大小，K为最大文本长度，E为嵌入维度）。
- 作用：提供生成图像的语义指导条件。
U-Net 扩散网络（Diffusion Model）
- 功能：在潜空间执行迭代去噪，生成包含语义信息的潜变量。
- 结构：
  - Encoder-Decoder 架构：包含下采样（压缩特征）和上采样（恢复细节）层。
  - 条件注入机制：
    - 时间步嵌入（Timestep Embedding）：控制不同去噪阶段的强度。
    - 空间变换器（Spatial Transformer）：通过交叉注意力（Cross-Attention）将文本嵌入与图像特征融合。其中，图像特征作为 Query，文本嵌入作为 Key/Value，实现图文语义对齐。
  - 跳跃连接（Skip Connections）：保留底层细节，避免信息丢失。
- 输入/输出：输入为带噪潜变量（维度 [B, Z, H/8, W/8]），输出为去噪后的潜变量（同维度）。
变分自编码器（VAE）
- 编码器（Encoder）：将原始图像（如 512×512×3）压缩到低维潜空间（如 64×64×4），降维至 1/8 分辨率。
- 解码器（Decoder）：将去噪后的潜变量解码为像素级图像（如 512×512×3）。
- 意义：大幅减少扩散过程的计算量（潜空间比像素空间小 64 倍）。

2.2 文生图工作流程详解

Stable Diffusion 的生成过程分为三个阶段（文生图）：

文本编码（Text Encoding）
- 输入提示词（如 “a cat on a sofa”）经 CLIP 编码为语义向量 $z_{text}$ 。
潜空间扩散与去噪（Latent Diffusion）
- 初始化：从高斯噪声采样生成初始潜变量 $x_{noise}$ （维度 64×64×4），它也是 $x_T$ 。
- 迭代去噪：
  - 条件注入：U-Net 结合文本嵌入 $z_{text}$ 和时间步信息，预测当前步的噪声 $ϵθ(xt,t,ztext)\epsilon_\theta(x_t, t, z_{text})$ 。
  - 去噪更新：通过采样器（如 DDIM、PLMS）逐步更新潜变量，公式简化如下：
    $xt−1=1αt(xt−1−αt1−αˉtϵθ(xt,t,ztext))+σtzx_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t, z_{text}) \right) + \sigma_t z$
    
    参数说明：
    - $x_t$ ：当前时间步 $t$ 的带噪图像（潜变量）。
    - $ϵθ\epsilon_\theta$ ：U-Net 预测的噪声（模型输出）。
    - $αt\alpha_t$ ：噪声调度参数，控制当前步的噪声强度（ $\alpha_t < 1$ ），由噪声调度策略计算得到，属于模型预配置的一部分。
    - $αˉt\bar{\alpha}_t$ ：累积噪声调度参数，定义为 $αˉt=∏i=1tαi\bar{\alpha}_t = \prod_{i=1}^{t} \alpha_i$ 。
    - $σt\sigma_t$ ：随机噪声的方差，通常取 $σt=(1−αt)(1−αˉt−1)/(1−αˉt)\sigma_t = \sqrt{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})/(1 - \bar{\alpha}_t)}$ ，也可以取 $1−αt\sqrt{1 - \alpha_t}$ 。
    - $ε_θ$ 为 U-Net 预测的噪声。
    - $z$ ：标准高斯噪声 $\sim \mathcal{N}(0, I)$ ，引入随机性。
  - 迭代次数：通常 20-50 步（远少于像素级扩散模型的 1000 步）。
图像重建（Image Decoding）
- 去噪后的潜变量 $x_0$ 输入 VAE Decoder，生成最终图像（512×512），过程为：将 $x_0$ 展平成一位向量、全连接升维、重塑特征图为三维张量、转置卷积上采样。过程示意图如下：

在这里插入图片描述

过程示意图

2.3 图生图工作流程详解

在 Stable Diffusion 中，图生图（img2img）与文生图（txt2img）共享同一个 U-Net 模型和噪声调度参数 $αt\alpha_t$ ，但两者的输入初始化方式和部分参数逻辑存在差异。尽管模型和调度参数相同，两种模式在输入构造和噪声强度控制上存在显著区别。

图生图模式中，原图通过 VAE 编码器压缩为潜变量 $z_0$ ，根据重绘强度（如 0.3）计算 $αˉt\bar{\alpha}_t$ ：
$αˉt=(1−s)2\bar{\alpha}_t=(1-s)^2$
$s$ 是重绘强度，s 越大，生成结果越偏离原图。若 s 为1，则 $xt\mathbf{x}_t$ 完全服从标准正太分布，整个过程和文生图没差，若 s 为0，则完全保留原图（无噪声添加）。

接下来是生成混合噪声：
$xt=αˉtx0+1−αˉtϵ,ϵ∼N(0,I)\mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})$
$xt\mathbf{x}_t$ 就是输入到 U-Net 模型中的初始潜变量，迭代去噪的步数由用户指定，过程和文生图的时候一致。

重绘强度 s 的设置：若是微调图像细节（如修复面部、调色），则 0.2-0.4 ；若是风格转换（如照片转油画），则 0.5-0.7 ；若是创意重构（如更换主体内容），则 0.8~1.0。

2.4 不同的采样方式区别

所谓采样方式，指的是根据 $x_{t}$ 得到 $x_{t-1}$ 的方式，采样过程输出的最终潜变量是 $x_0$ ，将其输入到 VAE Decoder 用于图像解码。

Stable Diffusion 中的采样方法（Sampler）是控制图像生成过程中潜变量迭代更新策略的核心组件，其数学本质是通过数值求解扩散逆过程，逐步将带噪潜变量 $z_t$ （即前面的 $x_{t}$ ）更新为更去噪的状态 $z_{t-1}$ （即前面的 $x_{t-1}$ ）。以下是常见采样方法的分类、公式解析及特点对比：

⚙️ 一、采样方法的数学本质

所有采样方法均基于以下通用更新公式：
$zt−1=1αt(zt−1−αt1−αˉtϵθ(zt,t))+σtϵz_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( z_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(z_t, t) \right) + \sigma_t \epsilon$

$ϵθ(zt,t)\epsilon_\theta(z_t, t)$ : U-Net 预测的噪声残差（受时间步 $t$ 和文本条件控制）
$αt,αˉt\alpha_t, \bar{\alpha}_t$ : 噪声调度器定义的信号保留系数 $αˉt=∏i=1tαi\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$
$σt\sigma_t$ : 随机噪声缩放因子
$ϵ\epsilon$ : 额外高斯噪声（仅随机性采样器添加）

不同采样器的差异体现在：

噪声预测的利用方式（如一阶/二阶近似）；
是否注入随机噪声 $ϵ\epsilon$ （决定收敛性）；
历史步长的参考数量（如单步/多步优化）。

🔬 二、主流采样方法分类与公式解析

📊 1. 基础确定性采样器（收敛型，没有随机噪声）

采样器	公式特点	优势	局限
Euler	一阶更新：仅用当前步噪声预测， $zt−1=f(zt,ϵθ)z_{t-1} = f(z_t, \epsilon_\theta)$	速度最快，20-30步可收敛	细节精度较低，高步数易过拟合
Heun	二阶校正：需两次噪声预测， $zt−1=zt−1αt(1−αt)(12ϵθ(zt,t)+12ϵθ(zt−12,t−1))z_{t-1} = z_t - \frac{1}{\sqrt{\alpha_t}} (1-\alpha_t) \left( \frac{1}{2}\epsilon_\theta(z_t,t) + \frac{1}{2}\epsilon_\theta(z_{t-\frac{1}{2}},t-1) \right)$	精度更高，减少伪影	速度慢2倍，显存消耗大
DDIM	非马尔可夫过程：支持跳跃更新， $zt−1=αˉt−1(zt−1−αˉtϵθαˉt)+1−αˉt−1ϵθz_{t-1} = \sqrt{\bar{\alpha}_{t-1}} \left( \frac{z_t - \sqrt{1-\bar{\alpha}_t} \epsilon_\theta}{\sqrt{\bar{\alpha}_t}} \right) + \sqrt{1-\bar{\alpha}_{t-1}} \epsilon_\theta$	10-15步生成可用图像，适合快速草图	高步数下细节不足

🎲 2. 随机性采样器（不收敛型）

采样器	公式特点	优势	局限
Euler a	添加随机噪声： $zt−1=Euler公式+σtϵz_{t-1} = \text{Euler公式} + \sigma_t \epsilon$	多样性高，适合创意生成	结果不可复现，可能扭曲细节
DPM++ SDE Karras	结合随机微分方程： $zt−1=DPM++基础+σtϵz_{t-1} = \text{DPM++基础} + \sigma_t \epsilon$	细节丰富，写实质感强	需30-40步，速度慢

⚡ 3. 高效多步采样器（平衡型）

采样器	公式特点	优势	局限
DPM++ 2M Karras	二阶多步法：引入预测器-校正器，参考历史步长优化更新	速度-质量平衡最佳，20-30步即可高质量收敛	对动漫风格可能过度锐化
UniPC	统一预测校正器： $zt−1=BH2变体z_{t-1} = \text{BH2变体}$ ，支持低阶最终采样	5-10步生成高质量图像，速度最快	高分辨率需选uniform skip type

⚠️ 4. 淘汰或不推荐采样器

PLMS：早期替代DDIM，稳定性差，易产生色块；
DPM fast：步数<20时可用，但质量不可控；
DPM adaptive：无视用户步数设置，耗时长且结果不稳定。

📊 三、关键参数对采样效果的影响

随机噪声注入（ $σtϵ\sigma_t \epsilon$ )：
- 收敛性：若 $σt=0\sigma_t = 0$ （如Euler、DPM++ 2M），结果可复现；若 $σt>0\sigma_t > 0$ （如Euler a），结果随机。
噪声调度器：
- Karras调度：优化后期降噪梯度，减少高步数下的伪影（如DPM++ 2M Karras）。
阶数（Order）：
- 二阶（2M）：平衡速度与精度；三阶（3M）：细节更精细但需>30步+低CFG（≤7）。

💎 四、总结：选择建议与典型场景

需求场景	推荐采样器	步数	关键特性
通用高质量	DPM++ 2M Karras	20-30	收敛快、细节适中，综合最优
极致写实细节	DPM++ SDE Karras	30-40	不收敛、细节丰富，适合人像/皮肤纹理
效率优先（草图）	UniPC / DDIM	5-15	极速生成，适合创意探索
多样性创意	Euler a	20-30	随机性强，适合角色设计/艺术创作
动画风格	LMS Karras	20-25	低饱和度、线条柔和，减少锐化瑕疵

操作技巧：

固定种子（Seed）时，收敛型采样器可复现结果，随机型需设 $η=0\eta = 0$ 抑制变化；
高分辨率（≥512×512）建议搭配 Karras 调度 或 UniPC uniform skip 避免细节异常[citation:8]。

采样器的本质是数值求解扩散逆过程的算法实现，通过调整更新策略平衡生成速度、质量与可控性，是连接扩散模型理论与工程落地的核心枢纽。

2.5 与 DALL·E 2 的结构对比

组件	Stable Diffusion	DALL·E 2
扩散空间	潜空间（VAE 压缩）	像素空间（直接生成）
条件控制	文本嵌入注入 U-Net 交叉注意力	双重条件（文本嵌入+图像嵌入）
先验模块	无	扩散先验（生成图像嵌入 `Z_i`）
计算效率	高（潜空间维度低）	低（像素空间计算量大）

2.6 设计优势与局限

优势：
- 效率高：潜空间去噪用的是64×64的像素，相比于512×512，减少 64 倍计算量，支持消费级 GPU 生成 512px 图像。
- 扩展性强：模块化设计支持图生图（Img2Img）、图像修复（Inpainting）等任务。
局限：
- 细节损失：VAE 压缩可能导致高频细节模糊。
- 属性绑定问题：复杂提示中物体属性易错位（如“红球在蓝盒子上”可能颜色颠倒）。