双塔模型 + 自监督学习：解决长尾物品表征难题

双塔模型的局限性

推荐系统中常见的头部效应导致少部分热门物品占据了大部分点击，而大部分物品的点击次数较低。这种不平衡的数据分布使得双塔模型在学习物品表征时存在以下问题：

• 热门物品表征学习好：由于热门物品的曝光和点击次数较多，模型能够获得足够的训练样本，从而学习到较好的表征。
• 长尾物品表征学习差：长尾物品由于曝光和点击次数较少，训练样本不足，导致其表征学习效果不佳。

为了解决这一问题，自监督学习通过数据增强（data augmentation）的方式，帮助模型更好地学习长尾物品的向量表征。

样本选择与纠偏

Batch 内负样本问题

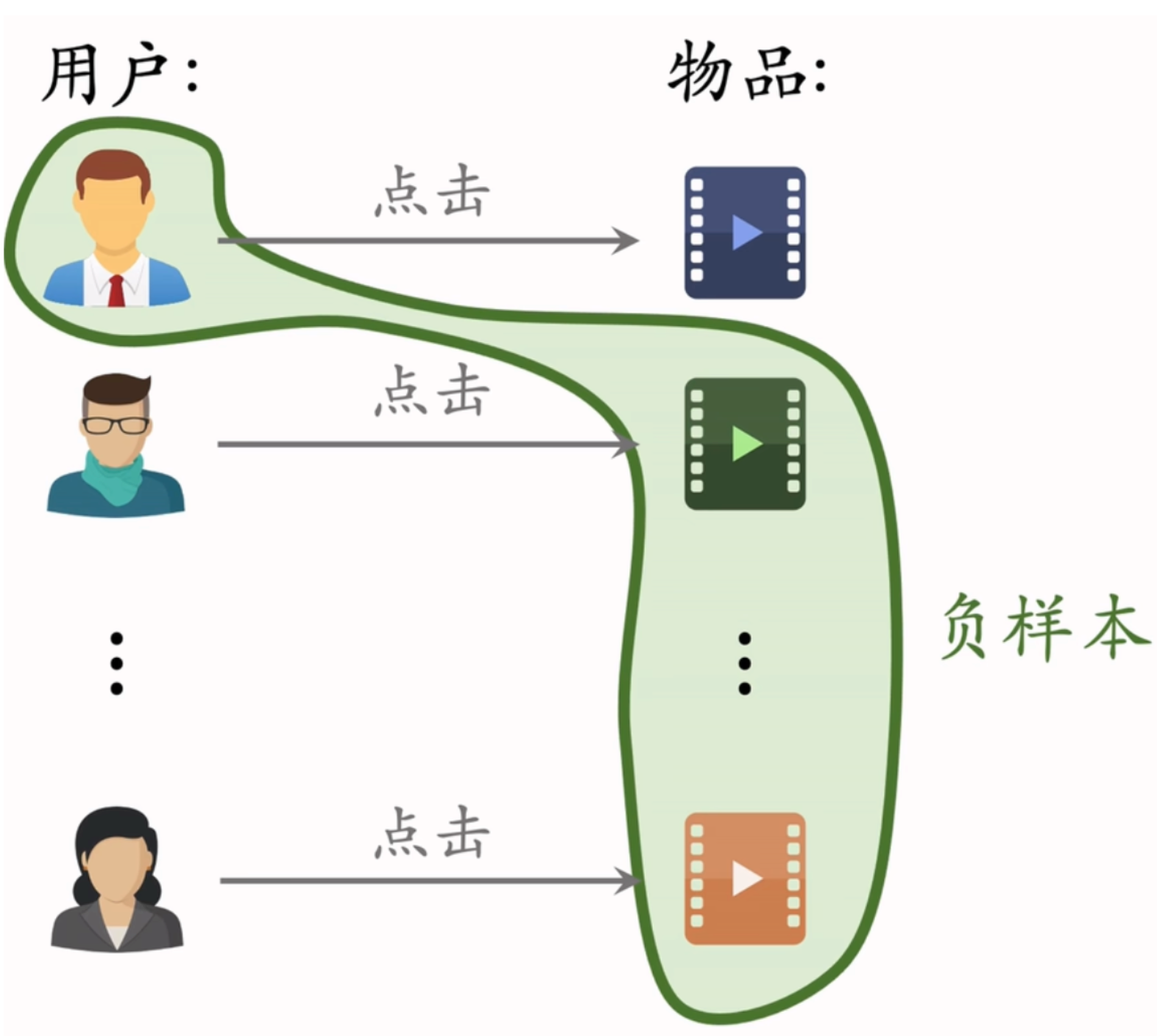
在传统的双塔模型中，Batch 内负样本的选中概率与点击次数成正比，这会导致热门物品被过度打压。为了解决这一问题，可以采用以下方法：

• 调整相似度计算：在计算用户向量和物品向量的相似度时，引入物品的点击概率 $p_i$，调整公式为：

  $$\cos (a_i,b_j)-\log (p_j)$$

  其中，$p_j$ 是物品 j的点击概率。

Listwise 训练方法

在 Batch 内，将每对用户-物品二元组视为一个正样本，其他用户-物品对视为负样本，形成一个 Listwise 训练方法。具体步骤如下：

• 对于一个 Batch 中的 n 对用户-物品二元组，形成 n 个列表，每个列表包含 1 个正样本和 n-1 个负样本。
• 鼓励正样本的相似度 $cos(a_i,b_i)$ 尽量大，负样本的相似度 $\cos (a_i,b_j)$尽量小。

双塔损失函数与自监督学习

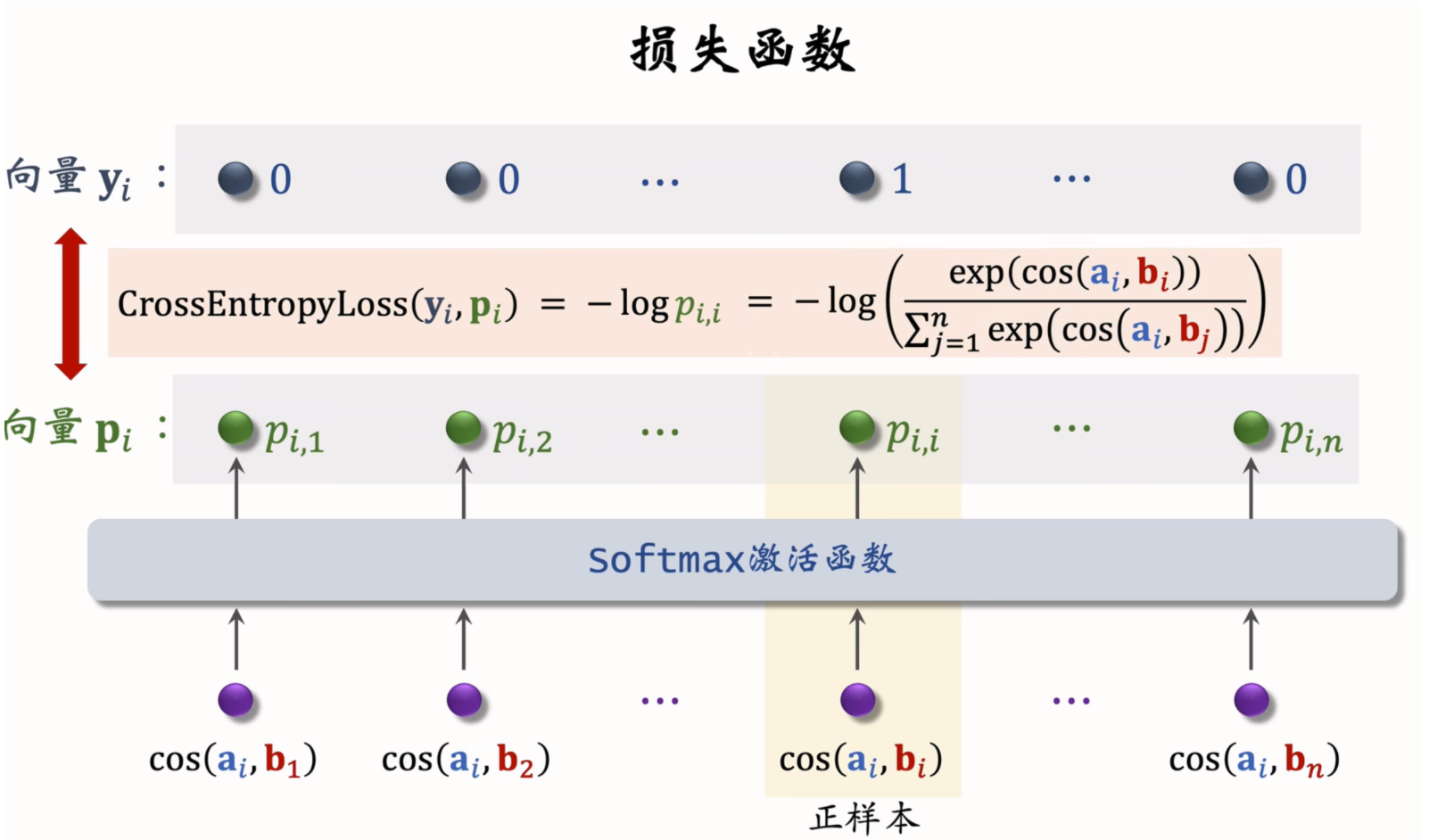
双塔损失函数

双塔模型的损失函数可以表示为：

$$L_{main}[i]=-\log \left(\frac{\exp (\cos (a_i,b_i)-\log p_i)}{{\sum }_{j=1}^n\exp (\cos (a_i,b_j)-\log p_j)}\right)$$

通过梯度下降减少损失函数：

$$\frac{1}{n}\sum _{i=1}^n{L}_{main}[i]$$

自监督学习

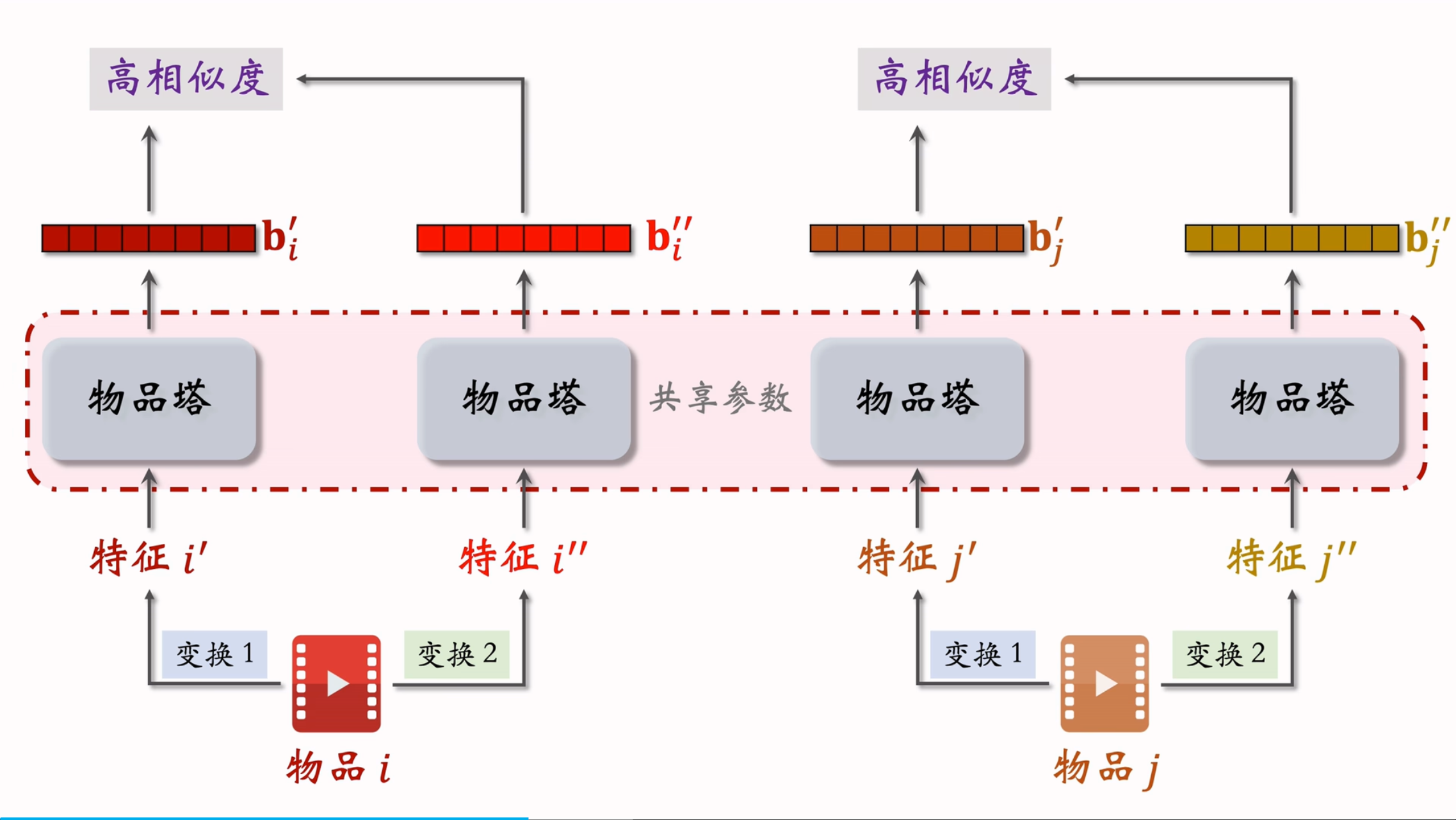
自监督学习通过数据增强的方式，对物品特征进行变换，生成不同的特征向量，从而更好地学习物品的表征。具体方法如下：

• 对物品 i特征进行变换1 和 变换2，得到特征 i’ 和 特征 i’‘,同理，对物品j也进行变换1和变换2得到特征j’和特征j’'，将这些特征使用同一个物品塔后得到特征向量 $b_i^{\prime },b_i^{\prime \prime },b_j^{\prime }，b_j^{\prime \prime }$，
• cos $b_i^{\prime },b_i^{\prime \prime }$ 和 $cos(b_j^{\prime }，b_j^{\prime \prime })$ 应该是高相似度，bi’和 bi’’ 对 bj’以及bj’’ 应该是低相似度,
• 鼓励相同物品的余弦相似度尽量大，不同物品的余弦相似度尽量小$cos(b_i^{\prime },b_i^{\prime \prime }),cos(b_i^{\prime },b_j^{\prime \prime })$尽量小

特征变换与训练

自监督学习的特征变换方法包括：

• Random Mask：随机丢弃某些特征。
• Dropout：仅对多值离散特征生效，随机丢弃部分特征值。
• 互补特征：将特征随机分成两组，分别生成物品表征。
• Mask 一组关联特征：基于特征之间的关联性，选择性地遮盖某些特征。

1. Random Mask（随机遮盖）

Random Mask 是一种简单的特征变换方法，通过随机遮盖某些特征来增强模型的鲁棒性。具体操作如下：

• 操作步骤：随机选择某些特征（如类别特征），并将它们设置为默认值（即遮盖）。
• 示例：
  • 假设某物品的类别特征为 U={数码，摄影}U = \{\text{数码，摄影}\}U={数码，摄影}。
  • 经过 Random Mask 后，类别特征变为 U′={default}U' = \{\text{default}\}U′={default}，即整个类别特征被丢弃。

这种方法可以模拟特征缺失的情况，增强模型对特征的依赖性，避免模型过度依赖某些特征。

2. Dropout（仅对多值离散特征生效）

Dropout 是一种广泛应用于神经网络的技术，通过随机丢弃特征值来增强模型的泛化能力。对于多值离散特征，Dropout 的具体操作如下：

• 操作步骤：随机丢弃特征中的部分值。
• 示例：
  • 假设某物品的类别特征为 U = {美妆，摄影}。
  • 经过 Dropout 后，类别特征变为 U’= {美妆}，即随机丢弃了部分特征值。

Dropout 可以减少特征之间的依赖性，增强模型对特征的鲁棒性。

3. 互补特征（Complementary Features）

互补特征 是一种通过随机分组特征来增强模型表征能力的方法。具体操作如下：

• 操作步骤：将特征随机分成两组，每组包含部分特征。
• 示例：
  • 假设用户有以下四种特征：ID、类别、关键词、城市。
  • 正常情况下，这些特征会被转换为 Embedding 并拼接起来，形成物品向量。
  • 随机分成两组：
    • 第一组：{ID, 关键词}
    • 第二组：{类别，城市}
  • 第一组的特征向量为：{ID, default, 关键词, default}
  • 第二组的特征向量为：{default, 类别, default, 城市}
  • 将这两组特征向量分别输入物品塔，鼓励它们的表征尽量相似。

这种方法可以增强模型对不同特征组合的表征能力，提高模型的泛化能力。

4. Mask 一组关联特征

Mask 一组关联特征 是一种基于特征关联性的特征变换方法。通过选择性地遮盖某些特征，可以增强模型对特征关联性的学习。具体操作如下：

• 特征关联性计算：使用互信息（Mutual Information, MI）计算特征之间的关联性。互信息公式为：

  $$MI(u,v)=\sum _{u\in U}\sum _{v\in V}p(u,v)\cdot \log \frac{p(u,v)}{p(u)\cdot p(v)}$$

  其中，p(u) 是特征 u 的概率，p(v) 是特征 v 的概率， p(u,v) 是特征 u 和 v 同时出现的概率。

• 操作步骤：

  • 假设总共有 ( k ) 种特征，离线计算特征两两之间的互信息，得到一个$k\times k$ 的矩阵。
  • 随机选择一个特征作为种子，找到与种子最相关的 $k/2$ 种特征。
  • 遮盖种子特征及其相关的 $k/2$ 种特征，保留其余的 $k/2$ 种特征。

• 示例：

  • 假设特征包括：受众性别 u ={男，女，中性} 和类目V = {美妆，数码，足球，科技 } 。
  • 计算互信息后发现，u = {女} 和 v = {美妆} 同时出现的概率较高，而u = {女}和 v = {数码} 同时出现的概率较低。
  • 选择 u = {女}作为种子特征，遮盖 u = {女} 和 v = {美妆} ，保留其他特征。

• 好处：比random mask、dropout、互补特征等方法效果更好

• 坏处：方法复杂，实现难度大，不容易维护（每添加一种特征，还需要算所有特征的mutual information）

自监督学习模型训练

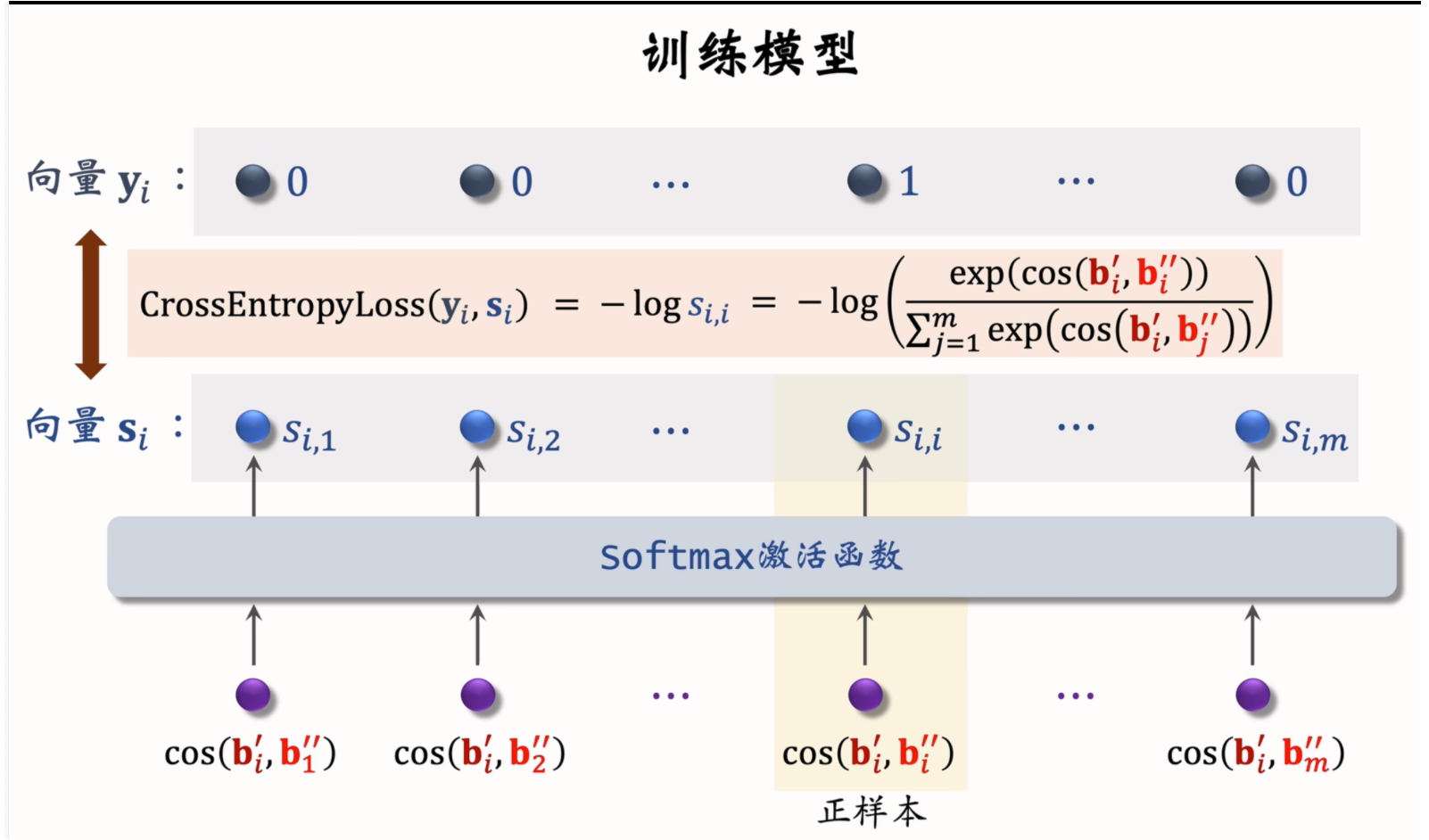
• 数据采样：从全体物品中均匀抽样，得到 m 个物品，形成一个 Batch。

• 特征变换：对每个物品进行两种特征变换，生成两组特征向量 $b_i^{\prime }$ 和 $b_i^{\prime \prime }$。

• 损失函数：计算每个物品的自监督学习损失函数：

  $$L_{self}[i]=-\log \left(\frac{\exp (\cos (b_i^{\prime },b_i^{\prime \prime }))}{{\sum }_{j=1}^m\exp (\cos (b_i^{\prime },b_j^{\prime \prime }))}\right)$$

• 梯度下降：通过梯度下降减少自监督学习的损失：

  $$\frac{1}{m}\sum _{i=1}^m{L}_{self}[i]$$

双塔模型+自监督学习结合

1. 双塔模型训练：

   • 从点击数据中随机抽取 n 对用户-物品二元组，形成一个 Batch。
   • 使用双塔模型的损失函数 $L_{main}$ 进行训练。

2. 自监督学习训练：

   • 从全体物品中均匀抽样，得到 m 个物品，形成另一个 Batch。
   • 对每个物品进行特征变换，生成两组特征向量。
   • 使用自监督学习的损失函数 $L_{self}$ 进行训练。

3. 联合训练：

   • 将双塔模型的损失和自监督学习的损失结合起来，进行联合训练：

     $$\frac{1}{n}\sum _{i=1}^n{L}_{main}[i]+\alpha \cdot \frac{1}{m}\sum _{j=1}^m{L}_{self}[j]$$

     其中，$\alpha$ 是一个超参数，用于平衡两种损失。

通过双塔模型与自监督学习的结合，可以更好地解决长尾物品表征学习的问题，提升推荐系统的整体性能。

小结

• 双塔模型学不好低曝光物品的向量表征
  • 但这不是模型问题，是数据问题，推荐系统存在头部效应，少部分占据了大部分曝光和点击
• 自监督学习：
  • 对物品做随机特征变换
  • 特征向量$b_i^{\prime }和b_i^{\prime \prime }$相似度高（相同物品）
  • 特征向量 $b_i^{\prime }和b_j^{\prime \prime }$相似度低（不同物品），就是尽量让表征分布在整个特征空间上，而不是集中在一起
• 实验效果：低曝光物品、新物品的推荐变得更准。

Reference

Shusen Wang. 推荐系统课程. Bilibili, 2023.