【专题十六】BFS 解决最短路径

📝前言说明：

• 本专栏主要记录本人的基础算法学习以及LeetCode刷题记录，按专题划分
• 每题主要记录：（1）本人解法 + 本人屎山代码；（2）优质解法 + 优质代码；（3）精益求精，更好的解法和独特的思想（如果有的话）
• 文章中的理解仅为个人理解。如有错误，感谢纠错

🎬个人简介：努力学习ing
📋本专栏：C++刷题专栏
📋其他专栏：C语言入门基础，python入门基础，C++学习笔记，Linux
🎀CSDN主页 愚润泽

你可以点击下方链接，进行该专题内不同子专题的学习

点击链接	开始学习
双指针(1)	双指针(2)
双指针(3)	双指针(4)
滑动窗口(1)	滑动窗口(2)
滑动窗口(3)	滑动窗口(4)
二分查找(1)	二分查找(2)
前缀和(1)	前缀和(2)
前缀和(3)	位运算(1)
位运算(2)	模拟算法
快速排序	归并排序
链表	哈希表
字符串	栈
队列 + 宽搜	优先级队列
BFS 解决 FloodFill	BFS 解决最短路径
多源 BFS	BFS 解决拓扑排序

题单汇总链接：点击 → 题单汇总（暂时未整理，因为还没刷完）

---

导论——BFS 解决最短路径

该专题只讲解：边权为 1 / 边权全都相同的最短路问题

最短路问题：

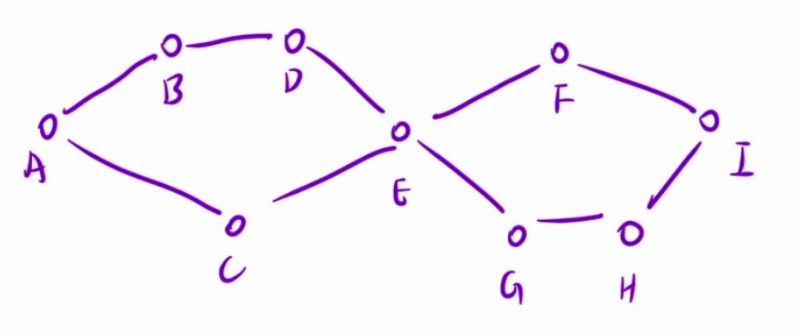
找从A 到 I 的最短的路径

解法：

• 从起点 A 开始做BFS，需要一个queue和hash
  • queue：用于层序遍历
  • hash：标记当前位置是否遍历过
    模拟：

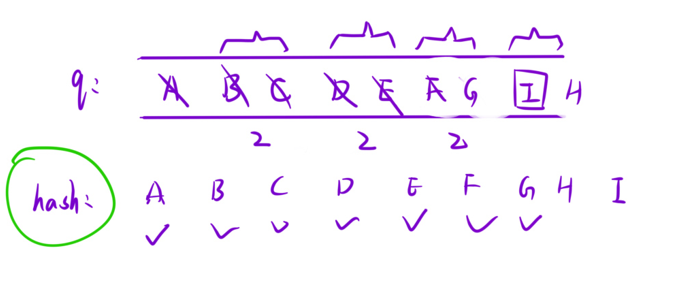
1. 去到一个点A，修改hash（入队时标记），出队时，把A能去的其他点（B, C）入队
2. 然后下一次弹出B，C（虽然这两点先后弹出，但是这两个点是同一层弹出的，即：同时向外扩展），然后把B，C能去的点加入（D，E）
3. 然后在弹出D的时候，因为E已经遍历过了（hash记录了），所以E不用重复加入（为什么不用加？因为从起点A到E的走法可能不同，但是都做到了从A到E，且从E开始，最后目标都是从E到 I（而后加E的肯定不是最优解））
4. 最后扩展层数的次数就是路径长度
5. 为什么最后结果就是最短路：因为我们在DFS的时候确保从起始点A开始，每条路都去走了，只不过在走的过程中长的路被淘汰了（hash淘汰的）

1926. 迷宫中离入口最近的出口

题目链接：https://leetcode.cn/problems/nearest-exit-from-entrance-in-maze/description/

优质解

屎山代码：

class Solution {
public:int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int nearestExit(vector<vector<char>>& maze, vector<int>& e) {int m = maze.size(), n = maze[0].size();queue<pair<int, int>> q;vector<vector<bool>> vis(m, vector<bool>(n, false));q.push({e[0], e[1]});vis[e[0]][e[1]] = true;int step = 0;while (q.size()) {step++;int sz = q.size();for (int j = 0; j < sz; j++) // 这里可不能写成 q.size(), 因为q 的大小是随循环变化的{ auto [a, b] = q.front();q.pop();for (int i = 0; i < 4; i++) {int x = a + dx[i], y = b + dy[i];if (x < m && x >= 0 && y < n && y >= 0 &&maze[x][y] == '.' && !vis[x][y]) {if (x == 0 || x == m - 1 || y == 0 || y == n - 1)return step;q.push({x, y});vis[x][y] = true;}}}}return -1;}
};

时间复杂度：$O(m\ast n)$
空间复杂度：$O(m\ast n)$

---

433. 最小基因变化

题目链接：https://leetcode.cn/problems/minimum-genetic-mutation/description/

个人解

屎山代码：

class Solution {
public:int minMutation(string start, string end, vector<string>& bank) {// 一次只能变化一个字符，并且变化后的字符串要在bank中// 难点在于怎么找下一次可以变化到的字符串: 遍历一遍 bank ？？？int n = bank.size();queue<string> q;vector<bool> vis(n, false);q.push(start);int ans = 0;while(q.size()){int sz = q.size();for(int i = 0; i < sz; i++){string cur = q.front();if(cur == end) return ans;q.pop();for(int j = 0; j < n; j++) // 遍历 bank 中每一个字符串{int diff = 0; // 记录两个字符串之间不同的字符个数for(int k = 0; k < 8; k++){if(cur[k] != bank[j][k]) diff++;}if(diff == 1 && !vis[j]){vis[j] = true;q.push(bank[j]);}}}ans++;  // 这一层扩展完了 ++}return -1;}
};

时间复杂度：$O(n\ast L)$，L是基因序列的长度
空间复杂度：$O(n)$

---

127. 单词接龙

题目链接：https://leetcode.cn/problems/word-ladder/description/

个人解

思路：

• 和上一题一样

屎山代码：

class Solution {
public:int ladderLength(string begin, string end, vector<string>& word) {int n = word.size(), len = begin.size();queue<string> q;vector<bool> vis(n, false);q.push(begin);int ans = 1;while(q.size()){int sz = q.size();for(int i = 0; i < sz; i++){string cur = q.front();q.pop();if(cur == end) return ans;for(int j = 0; j < n; j++){int diff = 0;for(int k = 0; k < len; k++){if(cur[k] != word[j][k])diff++;if(diff > 1) break;}if(diff == 1 && !vis[j]){vis[j] = true;q.push(word[j]);}}}ans++;}return 0;}
};

时间复杂度：$O(n\ast L^2)$
空间复杂度：$O(n)$

---

优质解

思路：

• 我们可以每次改原字符串的某一个位置，生成下一个可抵达的字符串，然后判断字符串是否在wordlist中
• 并且将wordlist中的字符串存入哈希表提高查找效率

代码：

class Solution {
public:int ladderLength(string beginWord, string endWord,vector<string>& wordList) {unordered_set<string> hash(wordList.begin(), wordList.end());unordered_set<string> vis; // 标记已经搜索过的单词if (!hash.count(endWord))return 0;queue<string> q;q.push(beginWord);vis.insert(beginWord);int ret = 1;while (q.size()) {ret++;int sz = q.size();while (sz--) {string t = q.front();q.pop();for (int i = 0; i < t.size(); i++) {string tmp = t;for (char ch = 'a'; ch <= 'z'; ch++) {tmp[i] = ch;if (hash.count(tmp) && !vis.count(tmp)) {if (tmp == endWord)return ret;q.push(tmp);vis.insert(tmp);}}}}}return 0;}
};

时间复杂度：$O(n\ast L^2)$
空间复杂度：$O(n\ast L)$

---

675. 为高尔夫比赛砍树

题目链接：https://leetcode.cn/problems/cut-off-trees-for-golf-event/description/

---

优质解

思路：

// 很有可能遇到一棵树，我先不砍，砍完其他树再回来砍，怎么知道这棵树砍还是不砍呢？
// 我们在每次砍树前，先确定下一个要砍的树的位置(因为要按顺序砍树)
// 然后求每次砍下一颗树的最短距离，把所有最短距离相加就是答案

代码：

class Solution {
public:int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};typedef pair<int, int> PII;bool vis[51][51];int m, n;int bfs(vector<vector<int>>& f, int st_x, int st_y, int en_x, int en_y) // 到指定点{queue<PII> q;memset(vis, false, sizeof(vis));  // 用这个 memset 比：多次开 vector 空间和初始化vector快q.push({st_x, st_y});vis[st_x][st_y] = true;int step = 0;while(q.size()){int sz = q.size();for(int i = 0; i < sz; i++){auto [a, b] = q.front();q.pop();if(a == en_x && b == en_y) return step;for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && f[x][y] != 0){vis[x][y] = true;q.push({x, y});}}}step++;}return -1; // 如果没办法到达就返回 -1}int cutOffTree(vector<vector<int>>& f) {m = f.size(), n = f[0].size();vector<PII> trees; // 先获得砍树顺序for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(f[i][j] > 1)trees.emplace_back(i, j); // 所有要砍的树的下标}}// 要排序sort(trees.begin(), trees.end(), [&](const PII& a, const PII& b){return f[a.first][a.second] < f[b.first][b.second]; // 代表升序排序});long long ans = 0;PII st = {0, 0};for(PII nxt: trees){int ret = bfs(f, st.first, st.second, nxt.first, nxt.second);if(ret == -1)return -1;ans += ret;st = nxt;}return ans;}
};

时间复杂度：$O(m^2\ast n^2)$
空间复杂度：$O(m\ast n)$

---

🌈我的分享也就到此结束啦🌈
要是我的分享也能对你的学习起到帮助，那简直是太酷啦！
若有不足，还请大家多多指正，我们一起学习交流！
📢公主，王子：点赞👍→收藏⭐→关注🔍
感谢大家的观看和支持！祝大家都能得偿所愿，天天开心！！！