2025年1中科院1区顶刊SCI-投影迭代优化算法Projection Iterative Methods-附完整Matlab免费代码

Projection-Iterative-Methods-based优化器（PIMO）是一种受投影迭代方法启发的新型元启发式算法。PIMO引入了四种新的算子来引导种群走向最优收敛，同时提高了探索和收敛速度。这种方法首次提出，集成了Kaczmarz和随机梯度下降等技术，以提高性能并防止收敛到局部最优。PIMO的有效性通过三组实验得到验证。PIMO是一种受投影迭代法启发的新型元启发式算法。于2025年7月在线发表、9月正式发表在JCR 1区，中科院1区 SCI 期刊 Knowledge-Based Systems。

1 提出的方法

1.1灵感来源

投影方法广泛用于约束优化，主要用于确保每次更新后的解满足约束条件。通过这种操作，可以避免优化过程中解违反约束而导致不现实的结果。特别是在具有复杂约束的非线性优化问题中，投影方法展现出独特优势。受此启发，本文设计了基于投影迭代方法的优化器(PIMO)。设目标函数为$f(x)$，其中$x\in {\mathbb{R}}^d$为解向量，约束集为$C$。优化问题可表述为：
$$\underset{x\in {\mathbb{R}}^d}{\min }f(x)\text{\hspace{1em}(1)}$$

在每次迭代中，通过投影操作将当前解$x_t^{(i)}$映射回约束集$C$：
$$x_t^{(reg(i)}=pro{j}_C\left(x^{(i)}\right)\text{\hspace{1em}(2)}$$

设当前函数值为$F_t=f(x_t)$，最优解为：
$$x_{test}=x_{test}^{(reg(i)},F_{test}=F_{test}^{(reg(i)}\text{\hspace{1em}(3)}$$

1.2 投影集群初始化

给定种群规模$N$和变量维度$D$，每个投影代理的初始化公式为：
$$X_{ij}={\tau }_0\times (U{B}_j-L{B}_j)+L{B}_j\text{\hspace{1em}(4)}$$
其中$L{B}_j=[b_1,b_2,...,b_{Dj}]$，$U{B}_j=[a{b}_1,a{b}_2,...,a{b}_{Dj}]$分别表示变量上下界。

1.3 残差引导投影(RGP)

RGP过程通过整合Kaczmarz行动作迭代更新策略与随机梯度下降(SGD)，建立协同混合框架。根据随机数${\tau }_1$和${\tau }_2$的比较结果选择策略：

$$X_{st},X_{st}=\{\begin{array}{ll}P=\frac{(F{)}^2}{{\sum }_{i=1}^n(F{)}^2}\to 1,& \text{若}{\tau }_1\ge {\tau }_2\\ F_t\to F_{test},& \text{否则}\end{array}\text{\hspace{1em}(5)}$$

当${\tau }_1\ge {\tau }_2$时，平方残差$(F{)}^2$的归一化概率分布$P\in [0,1]$使算法更关注误差较大区域。

解更新时使用的梯度信息$G_1$计算如下：
$$G_1=\{\begin{array}{ll}\frac{R\cdot (X_{st}-X_{test})+(1-R)\cdot (X_{st}-X_{test})}{2},& \text{若}\exists {\tau }_1\ge 2{\tau }_2\\ \frac{R\cdot (X_{st}-X_{test})+(1-R)\cdot (X_{st}-X_{test})}{2},& \text{否则}\end{array}\text{\hspace{1em}(6)}$$
其中$R,{\tau }_1,{\tau }_2$为[0,1]区间随机数。

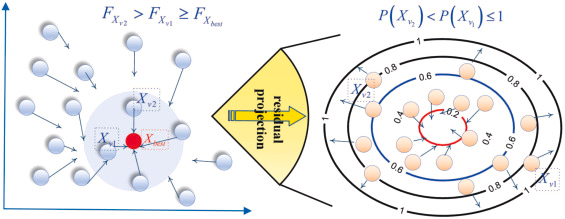
图2. RGP过程的选择策略示意图

雅可比矩阵$J$是描述非线性优化问题中解对输入变化敏感性的关键工具。对目标函数$f(x)$进行雅可比计算后，RGP能基于目标函数的局部线性化执行更精确的投影更新。

当目标函数$f(x)$输出$m$维向量且输入$x$为$n$维向量时，雅可比矩阵元素$J_{ij}$表示目标函数对变量$x_i$的偏导数：

$$J_{ij}=\frac{\partial f}{\partial x_i}\approx \frac{f\left(x+s{e}_i\right)-f(x)}{s}\text{\hspace{1em}(7)}$$

其中$f_j(x)$是目标函数的第$j$个分量，$e_i$是第$i$位为1的标准基向量，$s$为微小扰动值。通过扰动$x_i$计算每个分量的雅可比值：

$$J_{ji}=\frac{f_j\left(x_1,...,x_i+s,...,x_n\right)-f_j\left(x_1,...,x_n\right)}{s}\text{\hspace{1em}(8)}$$

最终形成$m\times n$维雅可比矩阵：
$$J=\left[\begin{array}{ccc}{J}_{11}& \cdots & J_{1n}\\ ⋮& \ddots & ⋮\\ J_{m1}& \cdots & J_{mn}\end{array}\right]$$

位置更新公式结合梯度与投影操作：
$$X_{ij}^{t+1}=\{\begin{array}{ll}{X}_i-\delta \times G_1,& \text{若 }3{\tau }_1\ge 2{\tau }_2\\ X_i+J\times \delta \times G_1^T,& \text{否则}\end{array}\text{\hspace{1em}(9)}$$

动态参数$\delta$随迭代变化：
KaTeX parse error: Expected '\right', got 'EOF' at end of input: …right) \tag{10}

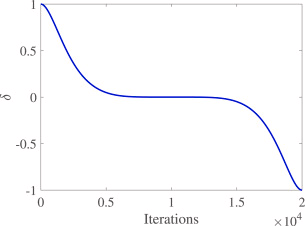
图3.动态衰减步长示意图

1.4 双重随机投影(DRP)

通过双重随机性增强算法全局搜索能力：

1. 随机选择两个索引$v_3$和$v_4$作为投影参考点：
   v3,v4=randi(N,2)∈{1,...,N}(11)v_3,v_4 = \text{randi}(N,2) \in \{1,...,N\} \tag{11}v3​,v4​=randi(N,2)∈{1,...,N}(11)

2. 梯度投影更新（当${\tau }_3\ge 2{\tau }_4$时）：
   $$\{\begin{array}{l}{g}_t=\frac{R\cdot (X_{v3}-X_{best})+(1-R)\cdot (X_{v4}-X_{best})}{2}\\ X_i^{t+1}=X_i-\delta \times g_t\end{array}\text{\hspace{1em}(12)}$$

3. 雅可比矩阵投影更新（当${\tau }_3<2{\tau }_4$时）：
   $$\{\begin{array}{l}{g}_t=\frac{R\cdot (X_{v3}-X_{best})+(1-R)\cdot (X_{v4}-X_{best})}{2}\\ X_i^{t+1}=X_i+J\times \delta \times g_t^T\end{array}\text{\hspace{1em}(13)}$$
   
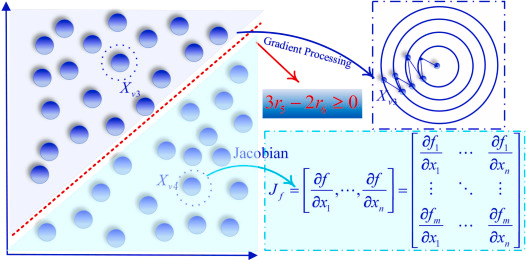
   图4 双重随机投影流程示意图

1.5 加权随机投影更新(WRPU)

加权随机投影更新是通过随机加权和自适应调节来引导粒子在解空间中向最优解移动的优化过程。该过程结合随机性和结构化投影，在探索过程中保持粒子的全局和局部特性平衡，从而提高优化效率。

• 随机因子生成：投影起点

决定粒子位置更新分量权重的随机因子$r_7$和$r_8$：
$$r_7=1+rand,r_8=1+rand\text{\hspace{1em}(14)}$$
这两个动态参数确保每次位置更新的多样性和不可预测性。

• 投影路径构建：多路径策略

粒子位置更新基于两种投影路径：

路径1：随机加权投影
$$X_{n3}^{proj(t+1)}=r_7\times X_i+(1-R)\times X_{best}+r_8\times (X_i-X_{best})\text{\hspace{1em}(15)}$$
通过随机权重$r_7$平衡当前位置$X_i$和目标位置$X_{best}$，扰动项$r_8$增强路径灵活性以跳出局部最优。

路径2：自适应校正投影
$$X_{n3}^{proj(t+1)}=X_i+\alpha \times (X_{n1}^{proj(t+1)}-X_{best})\text{\hspace{1em}(16)}$$
其中自适应因子$\alpha =(1-t/T)\times rand$随迭代调节步长：初期$\alpha \approx rand$支持全局探索，后期$\alpha \to 0$促进局部收敛。

维度因子$rand/j$决定路径选择：当$rand/j>rand$时选择路径1，其他情况选择路径2，随着维度$j$增加更倾向于选择稳定路径，保持高维解的稳定性。

1.5 Lévy飞行引导投影(LFGP)

通过模拟自然界生物的随机运动实现高效全局搜索和局部优化。

• 触发机制：Lévy投影概率
  $$P_{levy}=\frac{1}{2}\left(\tanh \left(9\times \frac{t}{T}-5\right)+1\right)\text{\hspace{1em}(17)}$$
  通过概率控制在不同迭代阶段触发：

• 初期：较低概率保留探索空间
• 后期：渐增概率加强最优解引导
  

1.6 Lévy飞行步长生成

$$\{\begin{array}{ll}z=\frac{u}{|v{|}^{1/\beta }},& \text{其中}u\sim N(0,{\sigma }_u^2),v\sim N(0,1)\\ {\sigma }_u={\left(\frac{\Gamma (1+\beta )\times \sin (\pi \beta /2)}{\Gamma ((1+\beta )/2)\times \beta \times 2^{(\beta -1)/2}}\right)}^{1/\beta }& \end{array}\text{\hspace{1em}(18)}$$
式中：$\beta$为[0,2]区间内的随机数，$v$为[0,1]区间内的随机数，$\Gamma$表示伽马函数

Lévy分布用于生成长尾随机步长，使粒子能在解空间中进行长距离跳跃，避免陷入局部最优解。该机制通过$\beta$参数控制步长分布形态，当$\beta$接近2时趋向高斯分布，接近0时呈现显著的长尾特性。

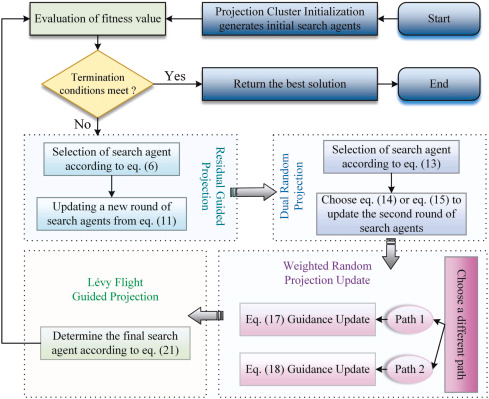
位置更新通过结合最优解$X_{Elite}$和当前解$X_i$实现，并采用随机权重动态调节：

$$d=rand\times (1-t/T{)}^2\text{\hspace{1em}(19)}$$
位置更新公式如下
$$X_{n4}^{proj(t+1)}=r_9\times X_{Elite}+(1-r_9)\times z\times d\times \left(X_{Elite}-X_i\times \left(2\frac{t}{T}\right)\right)\text{\hspace{1em}(20)}$$

其中：XElite=Best{Xn1proj(t+1),Xn2proj(t+1),Xn3proj(t+1)}X_{Elite} = Best\{X^{proj(t+1)}_{n1}, X^{proj(t+1)}_{n2}, X^{proj(t+1)}_{n3}\}XElite​=Best{Xn1proj(t+1)​,Xn2proj(t+1)​,Xn3proj(t+1)​}表示前三步最优粒子，$r_9$为[0,1]区间随机数，权重$d$随迭代逐渐减小，实现从全局搜索到局部收敛的过渡。

2、 完整代码

% Projection-Iterative-Methods-based Optimizer: A novel metaheuristic
% algorithm for continuous optimization problems and feature selection
function [Best_Score, Best_Pos, CG_curve] = PIMO(N, Max_iter, lb, ub, dim, fobj)Position = initialization(N, dim, ub, lb);  Fitness = zeros(N, 1);                    epsilon = 1e-6;alphabet = 1 : N;%% Record the initial optimal solution and fitnessfor i = 1:NFitness(i) = fobj(Position(i,:));      end[~, Ind] = sort(Fitness);     Best_Score = Fitness(Ind(1));Best_Pos = Position(Ind(1),:);CG_curve = zeros(1, Max_iter);% Store convergence information%% Main optimization loopfor it = 1:Max_iterdelta = sin(pi/2 * (1 - (2*it / Max_iter)).^5); % eq.(12)a = (1 - it/Max_iter) * rand(1, dim);for i = 1:Nrr1 = rand;rr2 = rand;if rr1 >= rr2Pr =  (Fitness.^2)/((norm(Fitness)^2));P = randsrc(1, 2, [alphabet; Pr']);P1 = P(1);P2 = P(2);elseP = Ind(1:2);P1 = P(1);P2 = P(2);endr = rand;J = Get_jacobian(fobj, Position(P1, :), epsilon); % Generalised Jacobi matrixif 3*rand >= 2*rand% eq.(14)grad = (r * (Position(P1, :) - Best_Pos) + (1-r) * (Position(P2, :) - Best_Pos)) / 2;pos_n1 = Position(i,:) - delta * grad;else% eq.(15)grad = (r * (Position(P2, :) - Best_Pos) + (1-r) * (Position(P1, :) - Best_Pos)) / 2;pos_n1 = Position(i,:) + delta * J * grad';endnewpos1 = max(min(pos_n1, ub), lb);fitt = fobj(newpos1);if fitt < Fitness(i)Fitness(i)= fitt;Position(i,:) = newpos1;endif rand > randP = randperm(N, 2); % eq.(13)P1 = P(1);P2 = P(2);if 3*rand >= 2*rand% eq.(14)grad = (r * (Position(P1, :) - Best_Pos) + (1-r) * (Position(P2, :) - Best_Pos)) / 2;pos_n2 = Position(i,:) - delta * grad;else% eq.(15)grad = (r * (Position(P2, :) - Best_Pos) + (1-r) * (Position(P1, :) - Best_Pos)) / 2;pos_n2 = Position(i,:) + delta * J * grad';endnewpos2 = max(min(pos_n2, ub), lb);fitt = fobj(newpos2);if fitt < Fitness(i)Fitness(i)= fitt;Position(i,:) = newpos2;endendfor j = 1 : dimr1 = 1+rand;r2 = 1+rand; % eq.(16)pho_1 = r1 * Position(i, :) + (1-r1) * Best_Pos + r2 * (Position(i, :) - Best_Pos); % eq.(17)pho_2 = Position(i,:) + a.* (newpos1 - Best_Pos); % eq.(18)pos_n3 = Position(i,:);if rand/j > randpos_n3(j) = pho_1(j);elsepos_n3(j) = pho_2(j);endnewpos3 = max(min(pos_n3, ub), lb);fitt = fobj(newpos3);if fitt < Fitness(i)Fitness(i)= fitt;Position(i,:) = newpos3;endend     endif rand <= 1/2*(tanh(9*it/Max_iter-5)+1)pos_n4 = zeros(1, dim);d=rand()*(1-it/Max_iter)^2;Step_length=levy(N, dim,1.5);Elite=repmat(Best_Pos, N, 1);r=rand;for i=1:Nfor j=1:dimpos_n4(j)=r*Elite(i,j)+(1-r)*Step_length(i,j)*d*...(Elite(i,j)-Position(i,j)*(2*it/Max_iter)); % eq.(21)endnewpos4 = max(min(pos_n4, ub), lb);fitt = fobj(newpos4);if fitt < Fitness(i)Fitness(i) = fitt;Position(i,:) = newpos4;endendend%% Record convergence curve[~, Ind] = sort(Fitness);     if Fitness(Ind(1)) < Best_ScoreBest_Score = Fitness(Ind(1));Best_Pos = Position(Ind(1),:);endCG_curve(it) = Best_Score;end
end
% Finite difference method for approximating generalised Jacobi matrix
function J = Get_jacobian(fobj, x, epsilon)
% f: handle to target function, accepts vector x
% x: current point (vector)
% epsilon: small perturbation valuen = length(x);fx = fobj(x);m = length(fx);J = zeros(m, n); % Calculate the finite difference in each direction according to eqs. (9) and (10).for i = 1:nx_perturbed = x;x_perturbed(i) = x_perturbed(i) + epsilon;f_perturbed = fobj(x_perturbed);J(:, i) = (f_perturbed - fx) / epsilon;end
end
function [z] = levy(n,m,beta)% beta is set to 1.5 in this papernum = gamma(1+beta)*sin(pi*beta/2);den = gamma((1+beta)/2)*beta*2^((beta-1)/2);sigma_u = (num/den)^(1/beta); % eq.(20)u = random('Normal',0,sigma_u,n,m);v = random('Normal',0,1,n,m);z =u./(abs(v).^(1/beta));
end
% Initialization function
function X = initialization(N, Dim, UB, LB)B_no = size(UB, 2); % number of boundariesif B_no == 1X = rand(N, Dim) .* (UB - LB) + LB;end% If each variable has a different lb and ubif B_no > 1X = zeros(N, Dim);for i = 1:DimUb_i = UB(i);Lb_i = LB(i);X(:, i) = rand(N, 1) .* (Ub_i - Lb_i) + Lb_i;endend
end

Dongmei Yu, Yanzhe Ji, Yiqiang Xia,Projection-Iterative-Methods-based Optimizer: A novel metaheuristic algorithm for continuous optimization problems and feature selection,Knowledge-Based Systems,Volume 326,2025,113978,https://doi.org/10.1016/j.knosys.2025.113978.