Leetcode——475. 供暖器


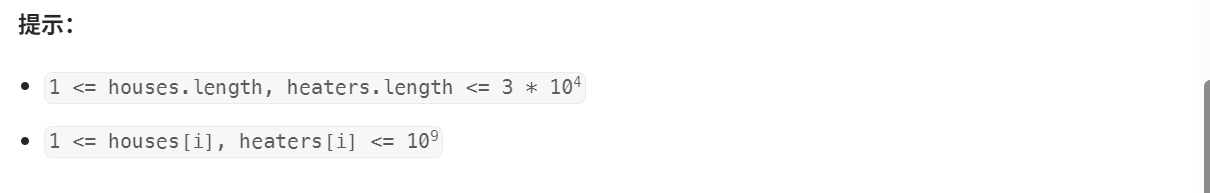
该题思路最重要的一点是从房子角度出发,寻找每一个最优的供暖器,取所有房子最优结果的最大值。如果从供暖器角度出发,则很难思考。
之后用两个变量分别指向房子数组和供暖器数组即可,整体依旧是双指针的经典思路。
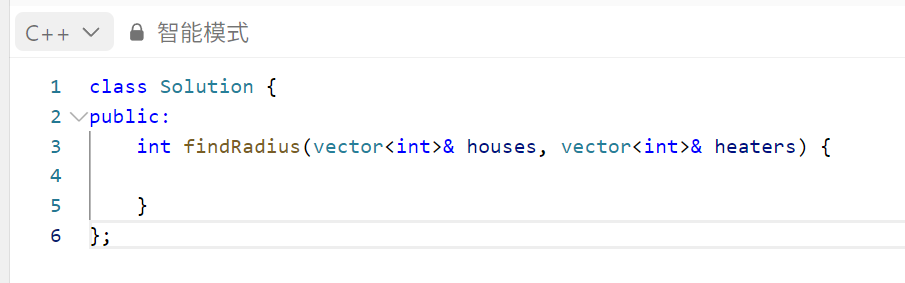
class Solution {
public:int findRadius(vector<int>& houses, vector<int>& heaters) {sort(houses.begin(), houses.end());sort(heaters.begin(), heaters.end());int l = 0, r = 0; // l -> houses r -> heatersint ans = 0;while(l < houses.size()){int house = houses[l];while(r + 1 < heaters.size() && abs(heaters[r + 1] - house) <= abs(heaters[r] - house)){r++;}ans = max(ans, abs(heaters[r] - house));l++;}return ans;}
};另一种二分解法,其实是基于暴力枚举的改进。
对于数据量来说,我们可以枚举所有半径可能性,取最优解。而最优解天然带有二分属性,即如果当前半径可以使供暖器覆盖所有房屋,则最优解一定在区间左半,否则最优解在右半。根据该思路,我们可以写出如下基本框架。
int findRadius(vector<int>& houses, vector<int>& heaters) {sort(houses.begin(), houses.end());sort(heaters.begin(), heaters.end());int l = 0, r = (int)1e9;while(l < r){int mid = l + ((r - l) >> 1);if(check(houses, heaters, mid)){r = mid;}else{l = mid + 1;}}return r;}之后的重点只需要放在check函数的实现上即可。
// 判断半径为radius时能否覆盖所有房屋bool check(vector<int>& houses, vector<int>& heaters, int radius){int n = houses.size(), m = heaters.size();// i -> houses j -> heatersfor(int i = 0, j = 0; i < n; ++i){while(j < m && heaters[j] + radius < houses[i]) { j++; } // 最小供暖器没覆盖if(j < m && heaters[j] - radius <= houses[i] && heaters[j] + radius >= houses[i]){continue; // j号供暖器可覆盖i号房屋, 继续检测i + 1号房屋}else{return false; // radius半径下存在 i 号房屋无法被覆盖}}return true;}check函数实质上依旧使用的是双指针,其更像是从供暖器角度出发,设立区间,遍历房屋,观察房屋是否在该区间上,进而判断当前半径是否有覆盖。
这种区间移动的思想起初自己并没有想到,而且只考虑到要枚举所有半径,的确没想到用二分来快速查找结果。
