LeetCode Hot 100：11. 盛最多水的容器

题目

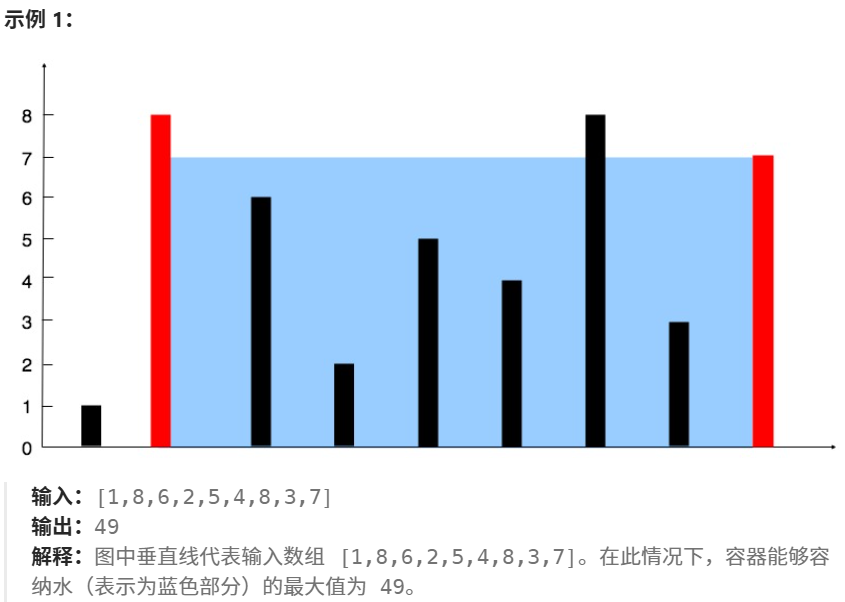
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。

说明：你不能倾斜容器。

解析

设双指针，左右指针分别在头和尾，初始化接水体积，且由于木桶效应，接水的高度取决于较短的那条边。

如果当前较高的那条边向中间移动：

1. 找到更短的边则跳过；

2. 找到更高的边，接水高度仍取为短边的值，由于宽度减少，接水体积仍会减少。

所以要让当前接水体积变大, 需要让当前较高高度的指针不动，尝试将指向较短高度的指针向中间收缩（尝试往中间找一个更高的高度，让决定接水高度的短边更高）。

如果计算出更大的容量，则更新接水体积。

step1: 要返回一个最大值，记为ans，初始化为0；
step1.2:计算ans
step2：初始化左右指针，一个初始化为开头，另一个初始化为尾端；
step3: 指针运行条件是left<right；
step4: 哪边短先移动哪边；
step5：决定在哪里插入ans；如果先移动指针再计算会跳过当前值，所以先将ans放入while后，判断条件前

来源：11. 盛最多水的容器 - 力扣（LeetCode）

答案

/*** @param {number[]} height* @return {number}*/
var maxArea = function(height) {let left = 0, right = height.length-1, ans = 0;    //初始化左右指针和接水体积while(left < right) {const area = (right - left) * Math.min(height[left], height[right]);    //当前体积ans = Math.max(ans, area);    //更新最大体积if(height[left] < height[right]) {    //决定接水高度的短边指针往中间移动，找更高的边left++;} else {right--;}}return ans;
};

复杂度分析

时间复杂度：O(n)，其中 n 为 height 的长度。

空间复杂度：O(1)，仅用到若干额外变量。