当前位置：首页 > news >正文

“菜鸟的java代码日记“ DAY3——跳跃游戏（中等）

news 2025/8/2 1:01:27

一、题目描述

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2：
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

二、题目分析

一开始我上来就分析怎么跳，是每次跳最远的还是直接0——>nums[0]——>nums[nums[0]]..后来想这两种跳法是不是结果一样，其实不是的。正确的思路应该是先分析停止的原因。

我们可以把数组分成两种情况：

1.数组中没有0：那肯定能到终点，你想，如果数组中没有0，那么这个数组最次就是【1,1,1,1，...1】，就相当于你一次往前走一步，那肯定能到终点啊。——>true

2.数组中有0：

1.如果数组长度为1，无论nums[0]是否为0，也一定是可以的，因为最小是0,0是起点也是终点——>true

2.数组长度不为1，且数组中有0，那么可能会出现下面两种情况：

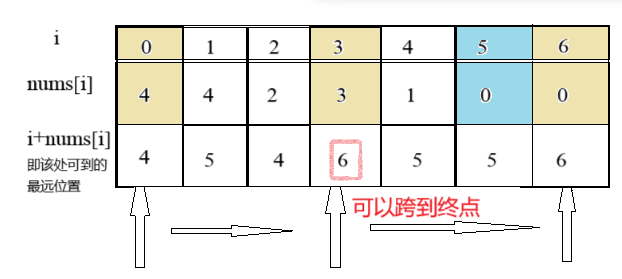
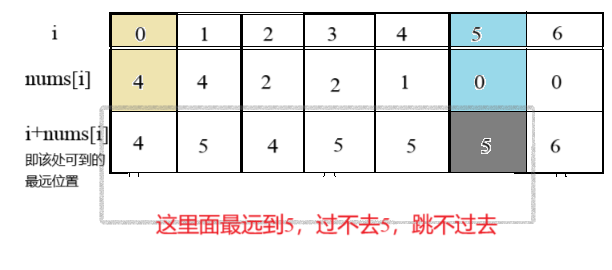
那么很明显，能不能到终点的就是看能不能跨过0（结尾的0不算，结尾的值不用管）；也就是只有是路中的0都能跳过去，我们就可以忽略0不看，也就是把它看成“没0”的情况；如果不可以跳过路中的0，那么一定会在0处卡死，卡死的特征就是上次走的位置和下次要走的位置是一个地方（不针对数组长度为1的情况）

三、总体梳理

停止的原因：

出现0的位置k之前所有位置（0——>k-1），都不能越过该处位置(k)；进一步来说，是下列情况或者位置时是不能越过该位置

☟

p：本次所在的位置

q：本次所在位置起跳，下次可到达的最远位置

p+1~q：下次所到达的位置的候选区域

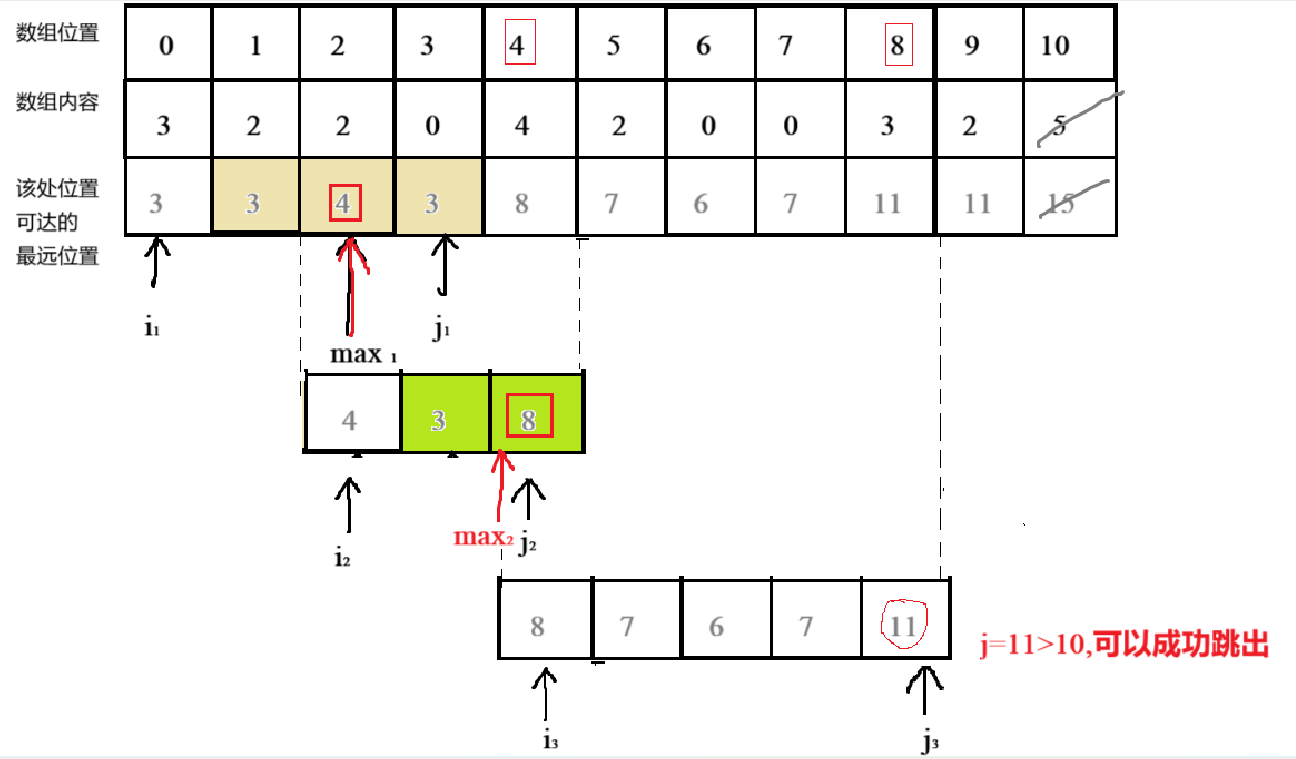
如果本次位置所可以到达的所有位置（下面的i=1,2,3,4）的可达位置（5,4,6,5）能够超过0所在位置（5）(更简单来说就是下下次所达到的最远位置超过0所在位置),那么一定可以跳过。

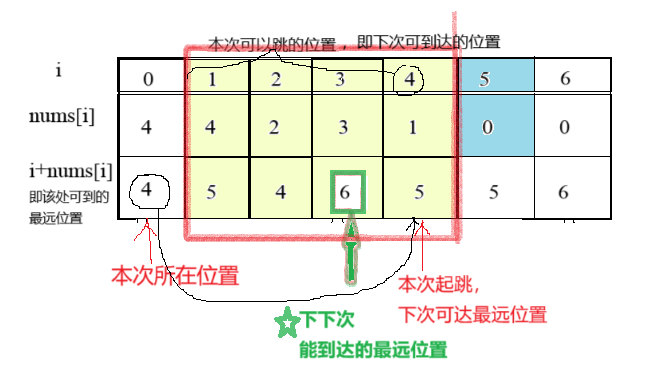
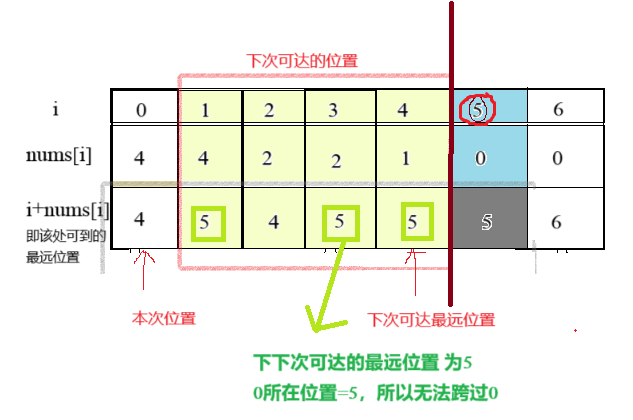
如果下下次能达到的最远位置超不过0所在位置，那么就肯定过不去，如上图所示。

最终合并的思路

上面只是分析了一下停止的原因，如果我们按照分析去写代码，会很复杂，我们不妨合并一下操作。（也就是只需要清楚，跳不过去的本质原因是0挡住了就行，上面就是分析为什么是0挡住了，为什么跳不过去0，以及说怎么跳如果过不去0那么所有方法都过不去。）

真正代码的核心：

无论是有0还是无0，我们都将下下次最远的地方作为下次的位置。
如果最终跳跃位置>=原数组长度——>成功跳出
如果本次的位置=下次跳跃的位置

代码详解：

普遍的过程/往前走的过程

从p=0出开始，第一次可达的最远距离是q=nums[0]+0处，那么寻找1~nums[0]中的k处，k处的num[k]+k是1到num[0]中比任意位置的 nums[*]+* （下下次）都大的地方，那么我们更新p,让他挪动到k处，更新q，让他挪动到p+nums[p]处，也就是p起跳可到达的最远处。同样寻找 p+1~q中的k，k=max（nums[p+1]+p+1,.....,nums[q]+q），即下下次最远的地方作为下次。更新p，让他挪到这一段的k处，更新q..........一直循环，

停止的条件：

1. q的位置>=nums.length——>成功跳出，提前终止循环，返回true。2. 上次的p位置=本次的p位置 或者 上次的q位置=本次的q位置    （都一样，因为p相同，q就相同 ）更加通俗的是p=q的时候（因为q=nums[p]+p,如果nums[p]=0，也就是卡在0处，那么q=0+p=p，当然要排出nums.length=1且nums[0]=0的情况）——————>卡死在0处，终止循环，返回false

四、代码写法

class Solution {public boolean canJump(int[] nums) {int i=0;//i相当于上文中的p，就是后面走的那个指针int j=nums[0];//j相当于上文中的q，就是前面走的指针int j1=-1;//这里是记录上次j（q）的位置int no=0;int max;if(nums.length==1){return true;}else{while(j<nums.length-1){max=-1;if(j1==j){no=1;break;}for(int k=i+1;k<=j;k++){if(nums[k]+k>max){max=nums[k]+k;i=k;}}j1=j;j=max;}if(no==1)return false;elsereturn true;}}
}