【图像处理】霍夫变换:霍夫变换原理、霍夫空间、霍夫直线、霍夫圆详解与代码示例
霍夫变换详解与代码示例
霍夫变换(Hough Transform)是一种用于检测图像中几何形状(如直线、圆)的特征提取技术。其核心思想是将图像空间中的点映射到参数空间(霍夫空间),通过累积投票机制识别形状。下面我将逐步推导原理、解释霍夫空间、详述直线和圆检测,并提供Python代码示例(使用OpenCV库)。
1. 霍夫变换原理
霍夫变换基于参数化思想:图像空间中的点对应霍夫空间中的曲线,而霍夫空间中的峰值对应图像中的几何形状。
- 基本推导(以直线为例):
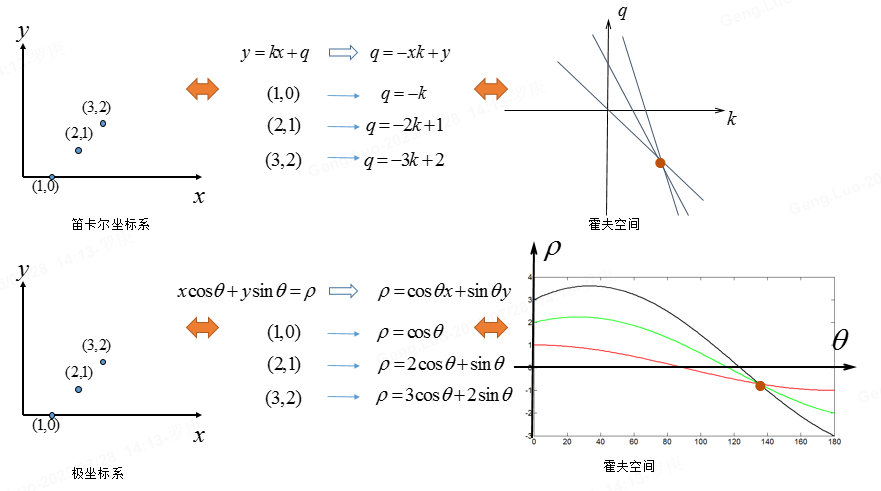
- 图像空间中,一条直线可表示为 y=mx+cy = mx + cy=mx+c,但此形式在垂直线时斜率 mmm 无限大,不实用。改用极坐标方程:
ρ=xcosθ+ysinθ \rho = x \cos \theta + y \sin \theta ρ=xcosθ+ysinθ
其中:- ρ\rhoρ 是原点到直线的垂直距离(ρ≥0\rho \geq 0ρ≥0),
- θ\thetaθ 是直线与x轴的夹角(0≤θ<180∘0 \leq \theta < 180^\circ0≤θ<180∘)。
- 图像空间中,一条直线可表示为 y=mx+cy = mx + cy=mx+c,但此形式在垂直线时斜率 mmm 无限大,不实用。改用极坐标方程:
-
图像空间中每个点 (xi,yi)(x_i, y_i)(xi,yi) 对应霍夫空间中的一条正弦曲线:ρ=xicosθ+yisinθ\rho = x_i \cos \theta + y_i \sin \thetaρ=xicosθ+yisinθ。
-
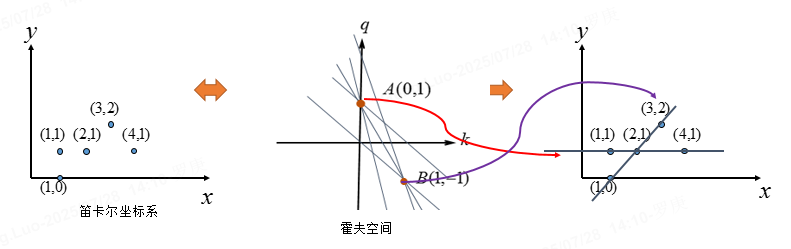
多个点共线时,它们在霍夫空间中的曲线相交于一点 (θk,ρk)(\theta_k, \rho_k)(θk,ρk),该点即为直线参数。
-
累积投票:将霍夫空间离散化为网格(累加器数组),每个点 (xi,yi)(x_i, y_i)(xi,yi) 对所有可能的 θ\thetaθ 计算 ρ\rhoρ,并在对应网格单元投票。峰值单元对应检测到的直线。
-
通用原理:
- 适用于任意参数化形状(如圆、椭圆)。
- 优点:对噪声和部分遮挡鲁棒;缺点:计算复杂度随参数维度增加(如直线是二维,圆是三维)。
2. 霍夫空间
霍夫空间是参数空间,用于累积投票:
- 定义:图像空间中的点映射到参数空间中的曲线或曲面。
- 量化:
- θ\thetaθ 范围:000 到 180∘180^\circ180∘(或 000 到 π\piπ 弧度),通常离散为 1∘1^\circ1∘ 步长。
- ρ\rhoρ 范围:−D-D−D 到 DDD(DDD 为图像对角线长度),离散为整数步长(如1像素)。
- 累加器:二维数组 A[θ][ρ]A[\theta][\rho]A[θ][ρ],初始为0。每个边缘点增加通过它的所有可能直线的投票数。峰值 A[θk][ρk]A[\theta_k][\rho_k]A[θk][ρk] 表示检测结果。
3. 霍夫直线检测
基于上述原理,检测图像中的直线:
-
步骤:
- 边缘检测:预处理图像(如Canny边缘检测),获取二值边缘图。
- 映射到霍夫空间:对每个边缘点 (xi,yi)(x_i, y_i)(xi,yi),遍历 θ\thetaθ(例如 θ=0∘,1∘,…,179∘\theta = 0^\circ, 1^\circ, \dots, 179^\circθ=0∘,1∘,…,179∘),计算 ρ=xicosθ+yisinθ\rho = x_i \cos \theta + y_i \sin \thetaρ=xicosθ+yisinθ,并累加 A[θ][ρ]A[\theta][\rho]A[θ][ρ]。
- 找峰值:设定阈值,A[θ][ρ]>阈值A[\theta][\rho] > \text{阈值}A[θ][ρ]>阈值 的单元对应检测到的直线。
- 转换回图像空间:用 (θk,ρk)(\theta_k, \rho_k)(θk,ρk) 绘制直线 ρk=xcosθk+ysinθk\rho_k = x \cos \theta_k + y \sin \theta_kρk=xcosθk+ysinθk。
-
优化:使用概率霍夫变换(Probabilistic Hough Transform),随机采样边缘点,减少计算量。
4. 霍夫圆检测
圆检测扩展了霍夫变换到三维参数空间:
- 圆方程:圆心 (a,b)(a, b)(a,b),半径 rrr,方程为:
(x−a)2+(y−b)2=r2 (x - a)^2 + (y - b)^2 = r^2 (x−a)2+(y−b)2=r2 - 霍夫空间:三维空间 (a,b,r)(a, b, r)(a,b,r)。
- 步骤:
- 边缘检测:获取边缘图。
- 梯度优化:利用边缘梯度方向减少计算:
- 边缘点 (xi,yi)(x_i, y_i)(xi,yi) 的梯度方向 ϕ\phiϕ 近似圆心方向。
- 对每个边缘点,沿梯度方向 ϕ\phiϕ 和 ϕ+180∘\phi + 180^\circϕ+180∘,在可能半径 rrr 范围内计算圆心 (a,b)(a, b)(a,b):
a=xi−rcosϕ,b=yi−rsinϕ a = x_i - r \cos \phi, \quad b = y_i - r \sin \phi a=xi−rcosϕ,b=yi−rsinϕ - 累加三维累加器 A[a][b][r]A[a][b][r]A[a][b][r]。
- 找峰值:设定阈值,A[a][b][r]>阈值A[a][b][r] > \text{阈值}A[a][b][r]>阈值 的单元对应检测到的圆。
- 挑战:三维空间计算量大,常使用多尺度或梯度方法优化。
5. 代码示例
使用Python和OpenCV实现霍夫直线和圆检测。需安装OpenCV:pip install opencv-python。
(a) 霍夫直线检测代码
import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像并转换为灰度
image = cv2.imread('input.jpg') # 替换为您的图像路径
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)# 边缘检测(Canny)
edges = cv2.Canny(gray, 50, 150) # 阈值50和150# 霍夫直线变换
# 参数:边缘图, rho精度(1像素), theta精度(1度), 阈值(投票数)
lines = cv2.HoughLines(edges, 1, np.pi / 180, 150) # 阈值调整以控制检测灵敏度# 绘制检测到的直线
if lines is not None:for line in lines:rho, theta = line[0]a = np.cos(theta)b = np.sin(theta)x0 = a * rhoy0 = b * rho# 计算直线端点x1 = int(x0 + 1000 * (-b))y1 = int(y0 + 1000 * (a))x2 = int(x0 - 1000 * (-b))y2 = int(y0 - 1000 * (a))cv2.line(image, (x1, y1), (x2, y2), (0, 0, 255), 2) # 红色直线# 显示结果
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('霍夫直线检测')
plt.axis('off')
plt.show()
(b) 霍夫圆检测代码
import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像并转换为灰度
image = cv2.imread('input.jpg') # 替换为您的图像路径
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
gray = cv2.medianBlur(gray, 5) # 中值滤波去噪# 霍夫圆变换
# 参数:输入图, 方法(HOUGH_GRADIENT), dp=1(累加器分辨率), minDist(圆心最小距离), param1(Canny高阈值), param2(累加器阈值), minRadius, maxRadius
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, dp=1, minDist=50,param1=50, param2=30, minRadius=10, maxRadius=100)# 绘制检测到的圆
if circles is not None:circles = np.uint16(np.around(circles))for circle in circles[0, :]:center = (circle[0], circle[1]) # 圆心radius = circle[2] # 半径cv2.circle(image, center, radius, (0, 255, 0), 2) # 绿色圆cv2.circle(image, center, 2, (0, 0, 255), 3) # 圆心红点# 显示结果
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('霍夫圆检测')
plt.axis('off')
plt.show()
代码说明:
- 输入图像:替换
'input.jpg'为您的图像路径(确保图像有清晰边缘)。 - 参数调整:
- 直线检测:
cv2.HoughLines的阈值控制最少投票数(值越大,检测越严格)。 - 圆检测:
param2是关键阈值(值越小,检测越多圆,但噪声增加)。
- 直线检测:
- 输出:显示原图叠加检测结果(直线为红色,圆为绿色带圆心红点)。
- 优化:实际应用中,可结合图像预处理(如高斯模糊)提高准确性。
霍夫变换是计算机视觉基础工具,广泛应用于车道检测、工业质检等领域。通过调整参数和优化方法,可平衡精度与效率。
总结
霍夫变换通过将图像空间映射到参数空间,有效检测几何形状。其核心是累加器投票机制,在霍夫空间中识别峰值。本示例展示了直线检测的实现,可扩展到其他形状(如圆)。实际使用时,建议结合图像优化(如降采样)以提高效率。如果您有特定图像或扩展需求,我可以进一步调整代码!
