红绿灯纵向距离的评估
1)针孔相机模型
基于相机内参和交通灯的像素尺寸,估算交通灯与相机的距离,核心原理是 针孔相机模型的相似三角形关系(距离 = 焦距 × 真实尺寸 ÷ 像素尺寸)。
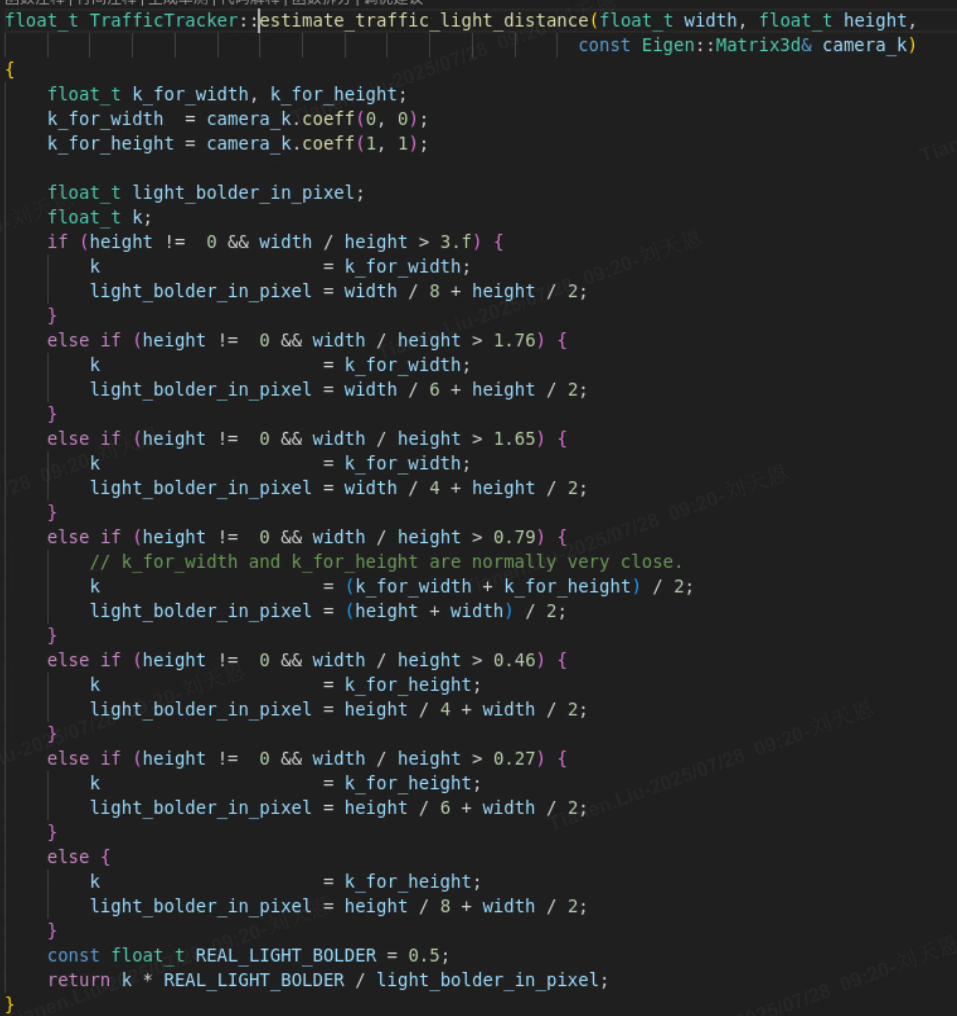


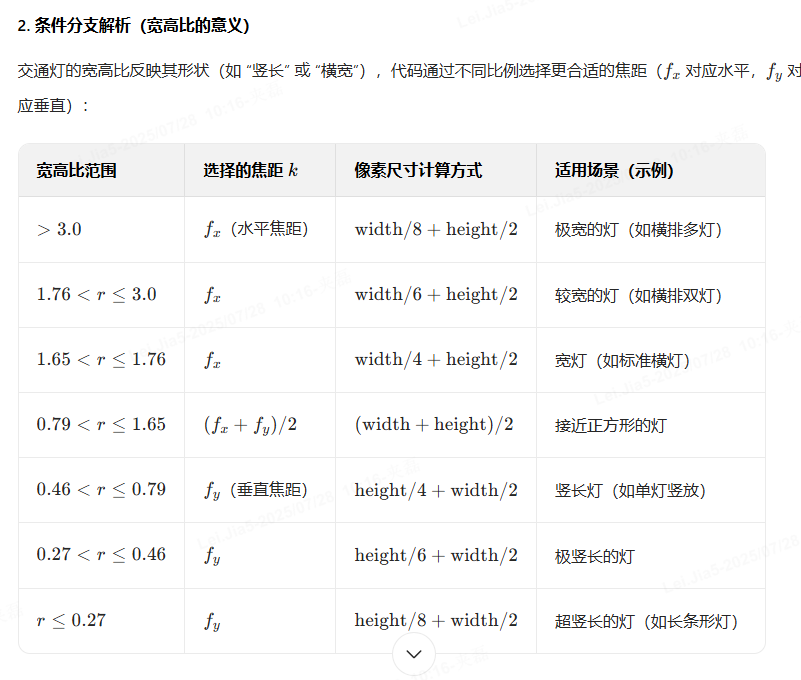

2)基于深度估计
“通过两帧目标的位置变化 + 相机参数,迭代猜深度,找最合理的结果”。
一、整体思路
想象你用手机拍同一棵树,第一次站 A 点,第二次站 B 点。通过树在两张照片里的位置变化,结合手机拍照的 “角度、位置” 参数,就能算树离你多远。代码里,摄像头就是手机,两次拍摄就是 A/B 点,目标(车、行人)就是树,步骤类似:
二、逐段解释
▶ 第一段:estimate_3d 主流程
void estimate_3d(...) {// 1. 过滤小目标:框太小(宽/高<32像素),检测不准,直接跳过if (obj2->region.rect.width < 32 || ...) return;// 2. 算相机和车的位置关系(位姿矩阵):// 记录两次拍照时,摄像头在车里的“位置+角度”,逆变换后,能把图像点转成世界坐标Eigen::Matrix4d world_cam_1 = (...ego位姿 × 相机位姿...).inverse();Eigen::Matrix4d world_cam_2 = (...同理...);// 3. 提取旋转(R1/R2:摄像头怎么歪的)和平移(T1/T2:摄像头在车里的位置)Eigen::Matrix3d R1 = world_cam_1.block<3,3>(0,0), R2 = ...;Eigen::Vector3d T1 = world_cam_1.block<3,1>(0,3), T2 = ...;// 4. 处理目标框的四个角:// 把目标框的左上、右上、右下、左下四个角找出来,乘以缩放比例ratio(还原图像真实尺寸)Eigen::Vector4d u1(0, obj1->width, obj1->width, 0); // 四个角的x坐标u1.array() += obj1->x; // 加上目标框的左边xu1.array() *= ratio; // 缩放// 5. 迭代猜深度:分三步(大步长粗找→中步长细化→小步长微调),调用find_best找最优深度dfloat d = find_best(...大范围内试d,步长10...);d = find_best(...细化范围,步长1...);d = find_best(...微调范围,步长0.1...);// 6. 把2D坐标转成3D(乘以深度d),再转到车的坐标系,记录目标在车前方多远(ego_x/y/z)Eigen::Vector3d pts3d(center_x*d, center_y*d, d); // 2D→3DEigen::Vector3d pt3d_cam = K.inverse() * pts3d; // 转到相机坐标系Eigen::Vector4d pt4d_world = camera2ego_pose * pt4d_cam; // 转到车坐标系obj1->ego_x = pt4d_world[0]; // 目标在车的x方向距离
}▶ 第二段:find_best 迭代猜深度
float find_best(...) {float min_L = 1e20; // 损失值,越小越好float min_d = -1; // 最优深度// 遍历所有尝试的深度d(从start到end,步长step)for (float d = start; d <= end; d += step) {float L = 0.0; // 当前d的损失// 遍历目标框的4个角(左上、右上、右下、左下)for (int i = 0; i < 4; i++) {// 过滤无效角点(超出图像范围,比如x≥3840像素,明显错了)if (u1[i]<0 || ...) continue;// 模拟旋转和平移:把角点按摄像头的旋转/平移变换,看是否符合两帧的变化Eigen::Vector3d A = R * p; // 旋转后的点// 计算损失:对比变换后的点和另一帧的角点,差异越小,d越准float a = pow(u,2) + pow(w,2);float b = 2*(u*v + w*z);float c = pow(v,2) + pow(z,2);float r = pow(A[2],2);float s = 2*A[2]*T[2];float t = pow(T[2],2);L += (a*d*d + b*d + c) / (r*d*d + s*d + t);}// 记录损失最小的dif (L < min_L) {min_L = L;min_d = d;}}return min_d; // 返回最优深度
}三、核心类比(帮你秒懂)
- 两次拍摄 → 你站 A 点和 B 点拍同一棵树。
- 目标框四个角 → 树的四个顶点(比如树冠的四个角)。
- 迭代猜深度 → 假设树离你 10 米、20 米…,看哪个距离下,“树在两张照片里的位置变化” 最合理(损失最小)。
- 坐标转换 → 把照片里的树的位置,转成 “离你多远、左边还是右边”(车的 ego 坐标系)。
四、代码的优缺点
| 优点 | 缺点 |
|---|---|
| 纯几何推导,不依赖 AI 模型,实时性好 | 依赖目标框检测准确(框不准→深度错) |
| 分三步迭代,兼顾速度和精度 | 只支持单摄像头,多摄像头融合能力弱 |
| 过滤小目标、无效坐标,鲁棒性较强 | 公式复杂,调试和维护成本高 |
简单说,这是一套 “用几何公式 + 迭代试错” 算深度的方法,适合对实时性要求高、不想依赖 AI 模型的场景(比如低成本自动驾驶、工业检测)。
一、主函数 estimate_3d:统筹全局的 “指挥官”
角色:接收两次拍摄的红绿灯数据(obj1、obj2)和相机参数,指挥各步骤计算深度。
关键步骤(以红绿灯为例):
“缩小图像” 准备:
ratio = 1/1408→ 把大图像缩成小尺寸(比如原图像 1408 像素宽,缩成 1 像素对应 1408 原像素),方便计算。“过滤小目标”:
如果第二次拍的红绿灯太小(宽 / 高 <32 像素),直接放弃(太小算不准)。“算相机位置变化”:
通过world_cam_1和world_cam_2,计算 两次拍摄时相机在世界中的位置和朝向(位姿矩阵)。- 类比:第一次拍时你站在 A 点,第二次站在 B 点,计算 A→B 的移动和转身。
“选四个角当‘线索’”:
取红绿灯边界框的 四个角(左上、右上、右下、左下),缩放后作为 “特征点”(ul、vl等)。- 类比:侦探标记目标的四个角,用它们的位置变化推理距离。
“算相对移动”:
用相机内参K处理,得到两次拍摄间的 相对旋转(转身)和平移(移动)(R和T)。“迭代试距离”:
分三步搜索深度d:- 第一步:大范围粗试(比如从
-10米到10米,步长 10 米); - 第二步:缩小范围细试(步长 1 米);
- 第三步:精准微调(步长 0.1 米)。
每次调用find_best找最优d。
- 第一步:大范围粗试(比如从
“转成车辆坐标”:
把算好的深度d转换成 车辆坐标系的 3D 位置(ego_x、ego_y、ego_z),过滤掉太近(<1 米)或太远(>7 米)的无效结果。
二、坐标转换:从 “照片点” 到 “现实位置”
角色:把图像中的红绿灯中心,转换成车辆坐标系的 3D 坐标。
关键步骤(以红绿灯中心为例):
“找图像中心”:
算红绿灯边界框的中心(center_x, center_y),缩放后乘以深度d,得到 相机视角下的 3D 点(pts3d)。- 类比:侦探知道 “照片中红绿灯在中间,假设它离相机
d米远,那么现实中它的位置是… ”
- 类比:侦探知道 “照片中红绿灯在中间,假设它离相机
“从相机视角转世界”:
通过相机内参的逆矩阵,把pts3d转到 相机坐标系;再通过位姿矩阵,转到 车辆坐标系(pt4d_world)。- 类比:把 “相机眼里的位置” 转换成 “车辆眼里的位置”(比如车前方 3 米、偏左 0.5 米)。
三、深度搜索 find_best:试错找最优距离
角色:模拟 “假设红绿灯在 d 米远,看两次照片的角点是否对齐”,找到最对齐的 d。
关键步骤(以一个角点为例):
“遍历候选距离”:
从start到end,按step试每个d(比如先试d=2米、d=3米…)。“过滤无效角点”:
如果角点超出图像范围(比如u<0或u>=3840),跳过(无效线索不算)。“模拟旋转和平移”:
假设红绿灯在d米远,用相对旋转R把第一次的角点 “转到第二次相机的视角”,得到A。“算对齐误差”:
对比 “模拟位置” 和 “第二次实际检测的角点”,算 水平差u、垂直差w、平移差v/z,再组合成 损失值(分子:误差的平方和;分母:防除零的保护项)。“选最优距离”:
记录所有d中 损失最小的那个(即角点最对齐的d)。
损失函数重点举例:
场景设定:手机拍两次杯子
你拿着手机,先站在位置 A拍了一张书桌前杯子的照片(左图),然后向前走了0.5 米到位置 B,又拍了一张(右图)。现在要算杯子离你有多远(深度d)。
步骤 1:标记角点
在两张照片里,找到杯子的同一个角(比如左上角):
- 左图(位置 A):角点坐标
(u1=100, v1=200)(像素)。 - 右图(位置 B):角点坐标
(u2=80, v2=200)(像素)。
步骤 2:假设一个距离d,模拟 “理论位置”
假设杯子离你 d=2米 远,我们要算:如果杯子真的在 2 米处,它在右图里应该出现在哪个位置?
数学模拟(代码里的R和T)
- 旋转
R:假设你移动时没转动手机(R是 “没转” 的矩阵,角点旋转后还是自己)。 - 平移
T:你向前走了 0.5 米(T=(0, 0, 0.5),z轴是深度方向)。
计算理论位置
- 把左图的角点转成 齐次坐标:
p = (100, 200, 1)(最后一个1是 “深度维度” 的占位符)。 - 用旋转
R处理:A = R * p→ 因为没旋转,A=(100, 200, 1)。 - 模拟平移后的差异:
- 水平差异
u:A(0) - A(2)*u2 = 100 - 1*80 = 20(理论和实际的水平差)。 - 垂直差异
w:A(1) - A(2)*v2 = 200 - 1*200 = 0(垂直方向没差异)。 - 平移的水平差
v:T(0) - T(2)*u2 = 0 - 0.5*80 = -40(平移带来的水平差)。 - 平移的垂直差
z:T(1) - T(2)*v2 = 0 - 0.5*200 = -100(平移带来的垂直差)。
- 水平差异
步骤 3:算 “误差分”(损失函数)
把差异做成 “评分公式”,评分越小,说明假设的d越接近真实距离: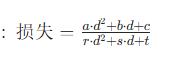
- 分子(误差大小):
a = u² + w² = 20² + 0² = 400(水平 + 垂直误差的平方和)。b = 2*(u*v + w*z) = 2*(20*(-40) + 0*(-100)) = -1600(交叉项,放大误差)。c = v² + z² = (-40)² + (-100)² = 11600(平移误差的平方和)。
- 分母(防除零保护):
r = A(2)² = 1² = 1(和深度相关的归一化项)。s = 2*A(2)*T(2) = 2*1*0.5 = 1(旋转和平移的交叉项)。t = T(2)² = 0.5² = 0.25(平移的深度平方项)。
代入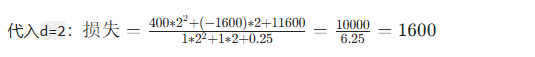
步骤 4:遍历找最优d
再试d=1米、d=3米… 计算它们的损失:
d=1:损失≈4622(比 1600 大,更差)。d=3:损失≈849(比 1600 小?不对,说明例子里的参数需要调整,核心是 真实深度下损失最小)。
实际中,当d等于真实距离时,损失会最小。代码会遍历所有可能的d(比如从 1 米试到 10 米,步长 0.1 米),找到损失最小的那个d。
