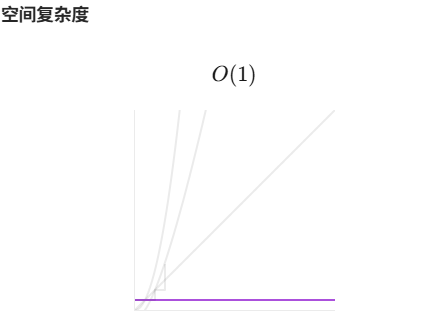
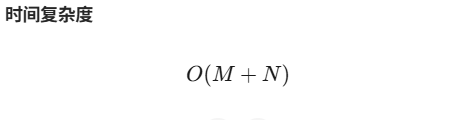【LeetCode】算法详解#10 ---搜索二维矩阵II
1.题目介绍
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
2. 解决思路
一个m行n列的矩阵,要求判断其中是否存在特定值,已经知道了这个矩阵的特点:从左向右依次增大,从上至下依次增大。最容易想到的做法就是直接遍历,但时间复杂度为m*n,或者是对每一行采用二分查找,时间复杂度为mlogn。题目要求采用一个高效的方法,那么现在观察矩阵的特点,对于一个元素[x][y],一定有:在他同行左侧的元素比他小,在他同列下侧的元素一定比他大。根据这个规律,我们可以从右上角开始,通过不断判断目标值与当前位置的大小关系,并不断改变坐标来寻找是否元素存在。如果索引越界,则表示元素不存在。
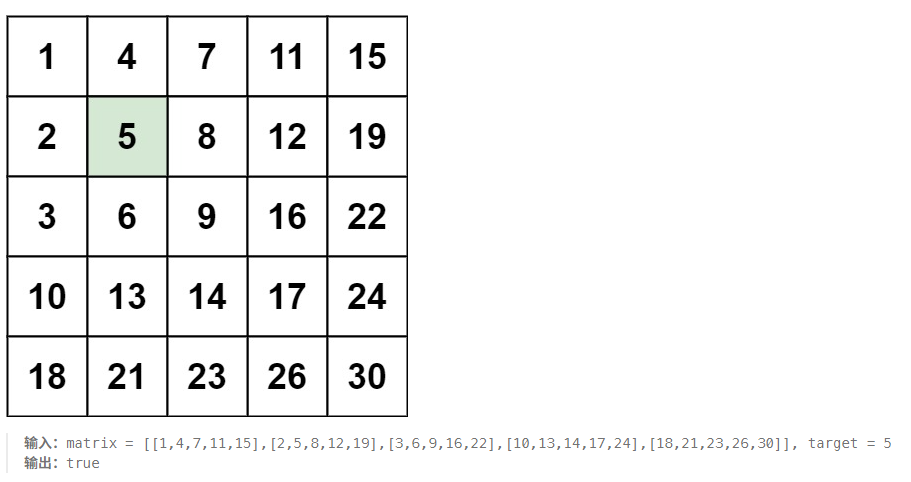 3.步骤讲解
3.步骤讲解
1.定义变量m表示矩阵行数,n表示矩阵列数
2.定义变量x,y,表示元素索引,从矩阵右上角开始
3.当元素索引不越界时,即x<m且y>=0时,进行循环查找
4.如果目标值等于当前值时,返回true
5.如果目标值大于当前值,将行索引+1,与较大值匹配。反之将列索引-1,与较小值比较
6.循环退出时,也就是索引越界时,则表示元素不存在,返回false
4.代码展示
public static boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length;int n = matrix[0].length;//从右上角开始int x = 0;int y = n-1;//索引不越界时while (x < m && y >= 0){//如果目标值匹配,返回trueif (target == matrix[x][y]){return true;}//如果目标值大于当前值,则向下查找,反之向左查找if (target > matrix[x][y]){x++;}else {y--;}}return false;}5.执行结果
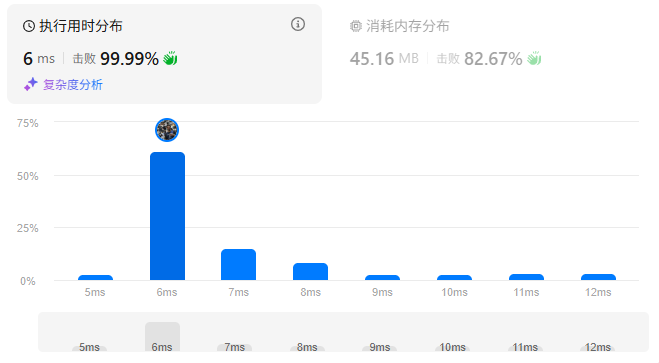
在leetcode中测试用例平均耗时6ms
内存分布45.16MB