决策树算法小结(上)
一、决策树概念
决策树属于归纳法。决策树模型是一种描述对实例进行分类的树形结构。
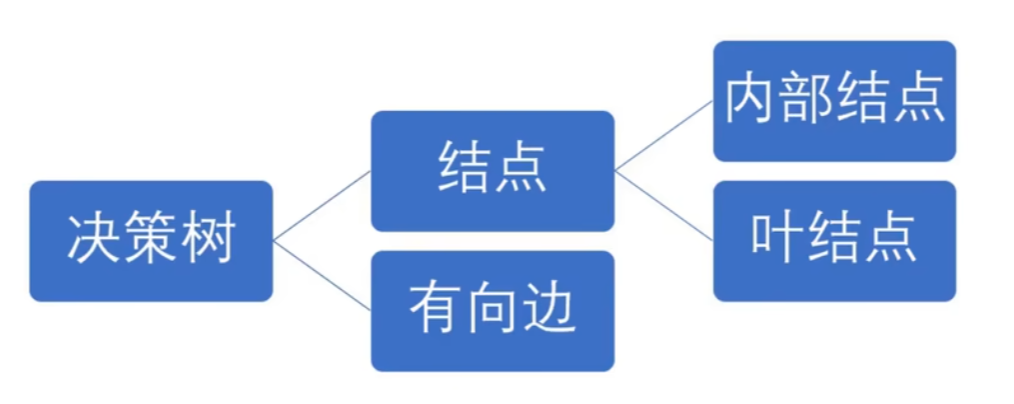
内部节点表示属性/特征,叶结点表示类别。
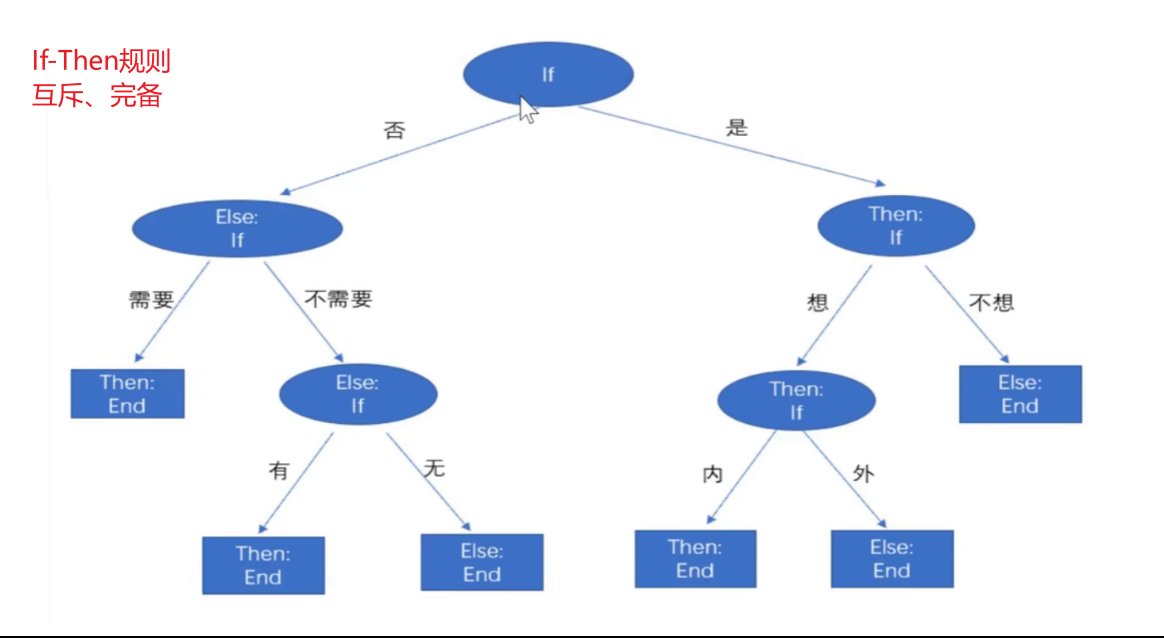
构建决策树
- 构建根节点
- 选择最优特征,一次分割训练数据集
- 若自己被基本正确分类,构建叶节点,否则,继续选择新的最优特征。
- 重复以上两部,知道所有的训练数据子集被正确分类
最优特征如何选择?
??????????
决策树:给定特征条件下类的P(Y|X)---------分类,Y表示类别,X表示特征
条件概率分布:特征空间(有特征向量组成,用来表示每一个输入的实例)的一个划分
划分:单元或区域互不相交
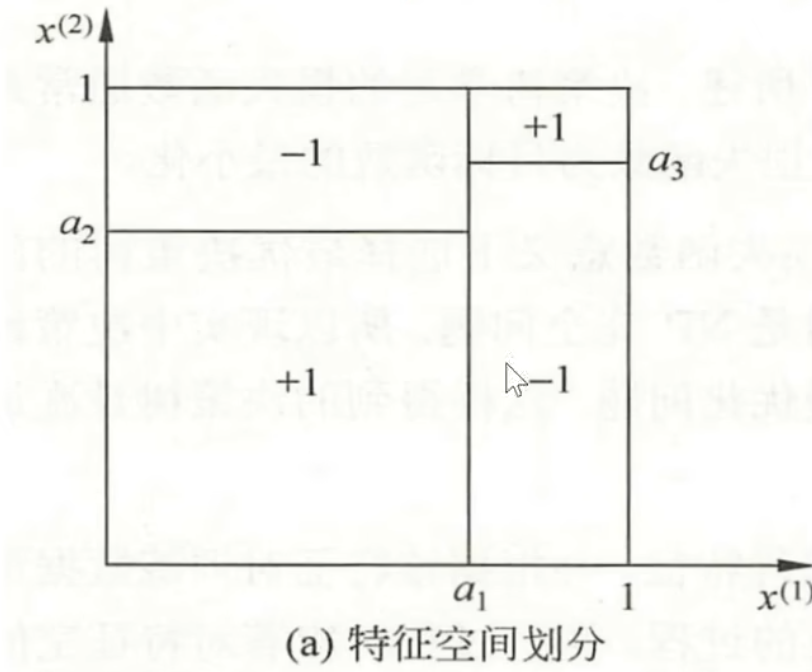
决策树的概率分布理解:一条路径对应划分中的一个单元,决策树的条件概率分布由各个单元给定条件下类的条件概率分布组成。
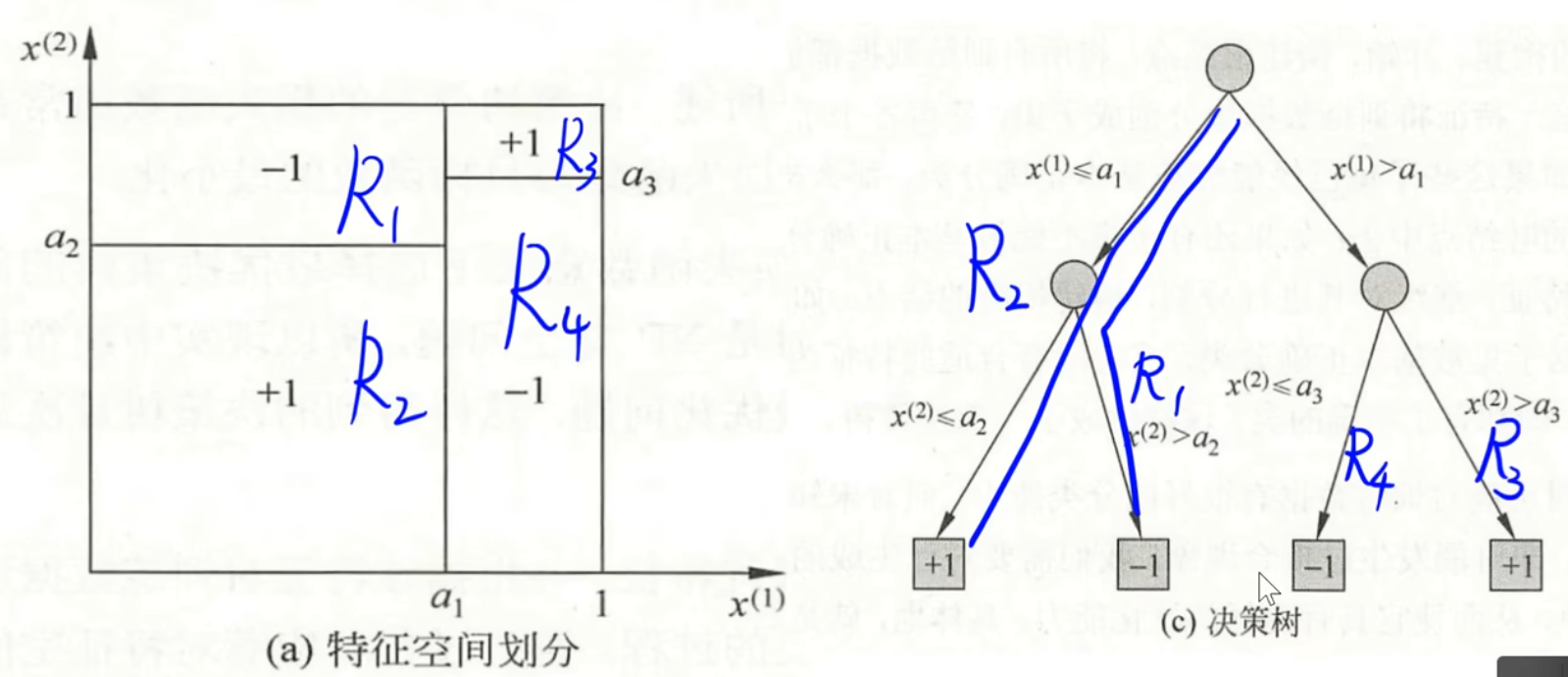
二、决策树学习
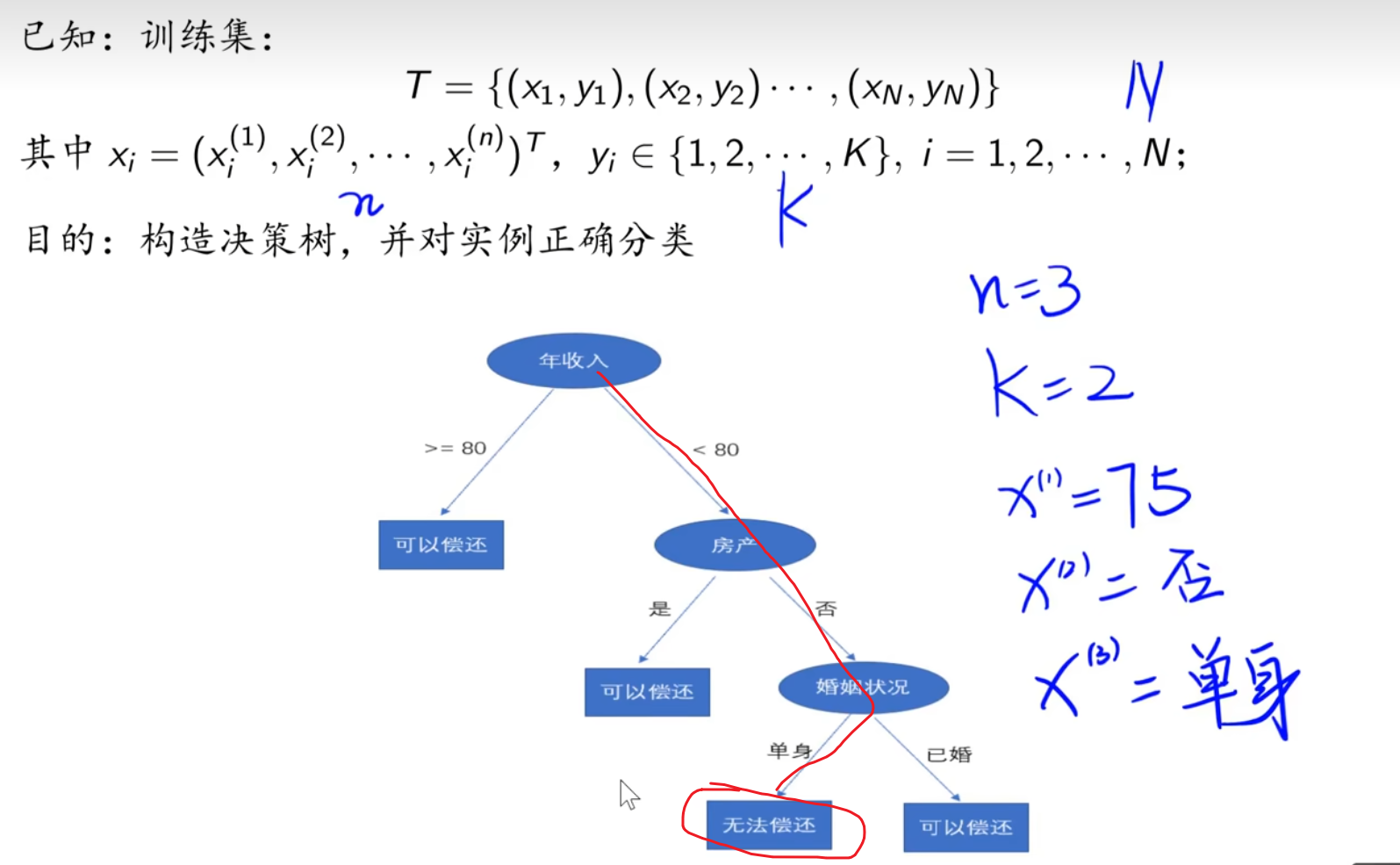
本质:从训练数据集中归纳出一组分类规则,与训练数据集不相矛盾
假设空间:由无穷多个条件概率模型组成
一颗好的决策树:与训练数据矛盾较小,同时具有很好的泛化能力
策略:最小化损失函数
特征选择:递归选择最优特征
生成:对应特征空间的划分,知道所有训练子集被基本正确分类
剪枝:避免过拟合,具有更好的泛化能力。
三、决策树特征选择
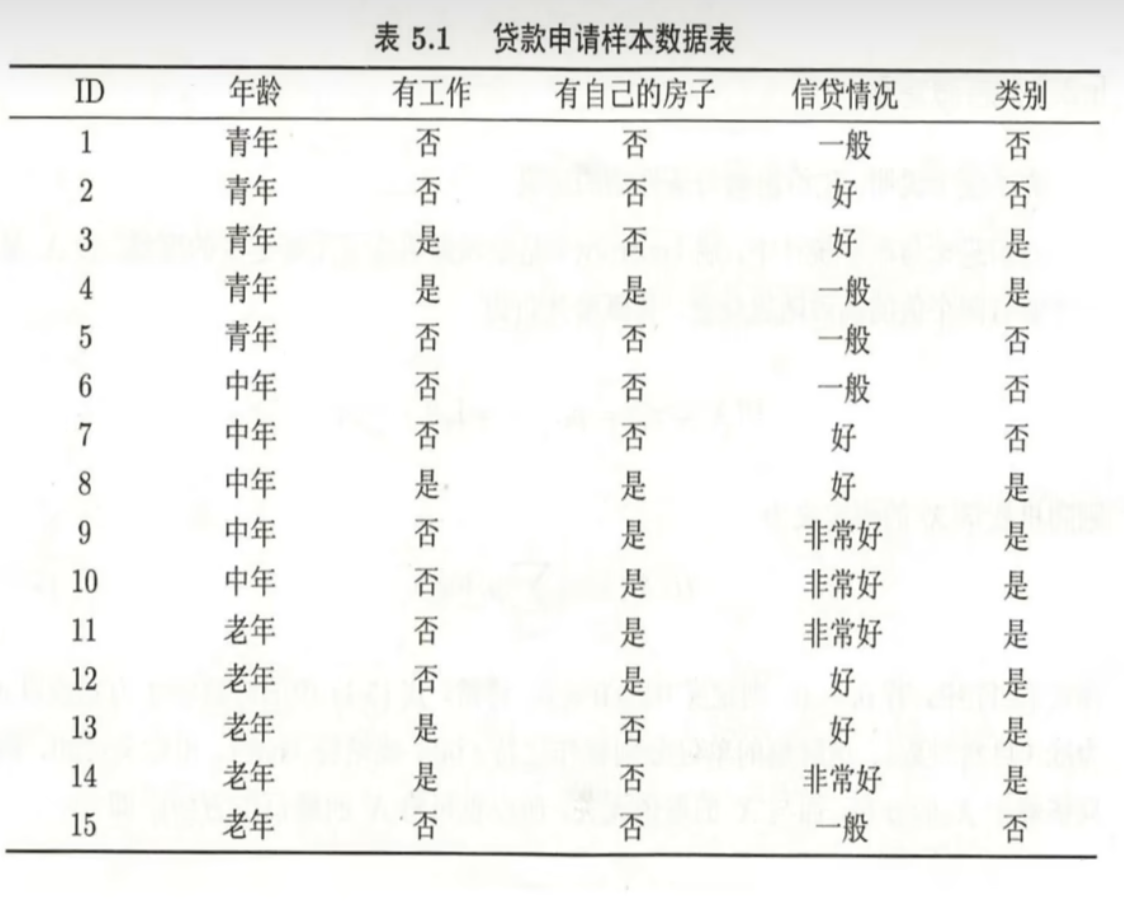
选择年龄为根节点建立决策树
选择工作为根节点建立决策树 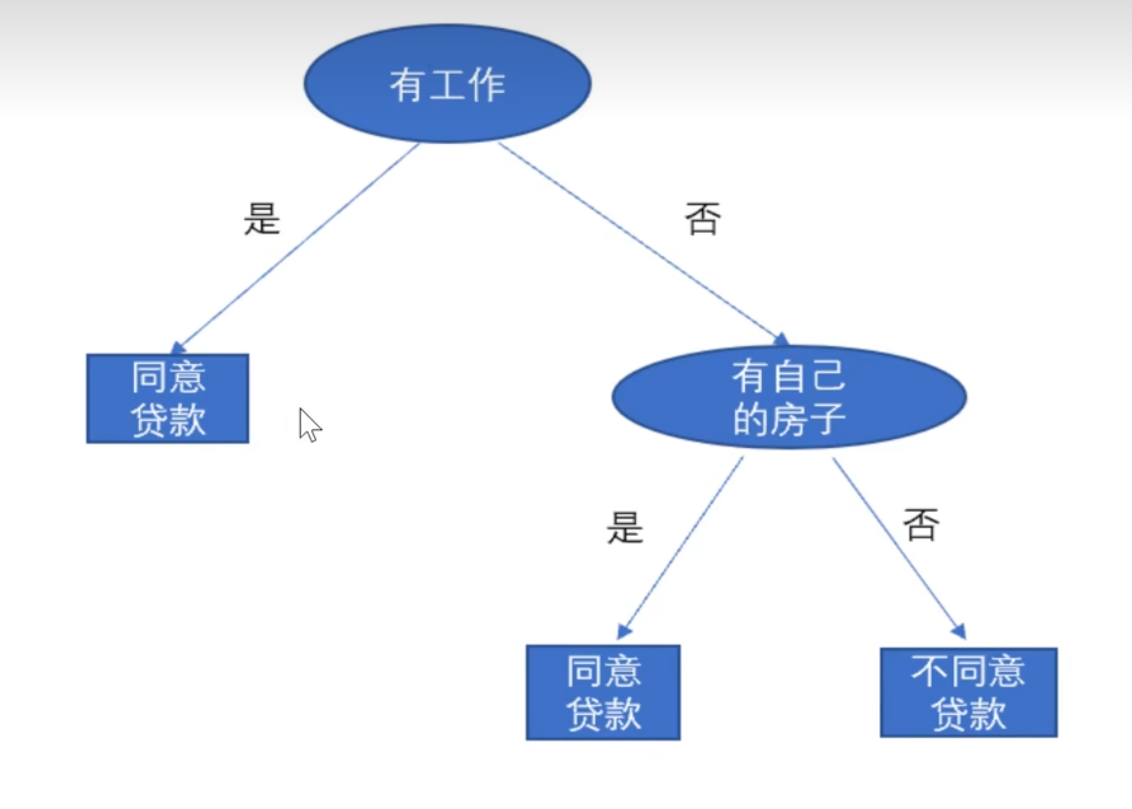
选择根节点不同,模型也不一样。因此利用信息增益来进行特征选择。
3.1信息增益
信息论中熵的概念。熵度量了事物的不确定性,越不确定的事物,它的熵就越大。具体的,随机变量X的熵的表达式如下:
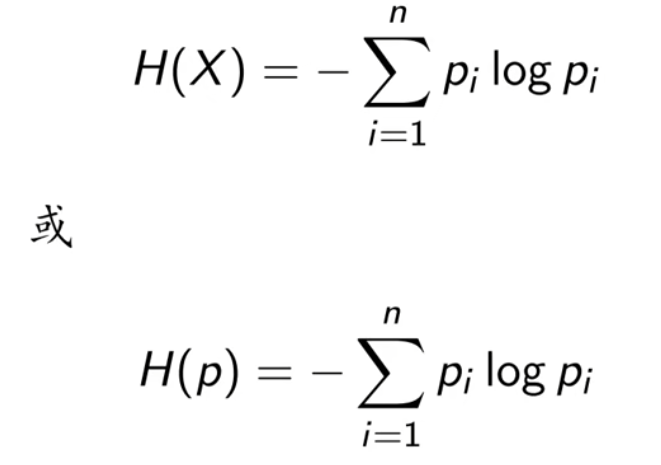
随机变量的取值等概率分布的时候,相应的熵最大。 其中n代表X的n种不同的离散取值。而pi代表了X取值为i的概率,log为以2或者e为底的对数。举个例子,比如X有2个可能的取值,而这两个取值各为1/2时X的熵最大,此时X具有最大的不确定性。值为H(X)=−(12log12+12log12)=log2。如果一个值概率大于1/2,另一个值概率小于1/2,则不确定性减少,对应的熵也会减少。比如一个概率1/3,一个概率2/3,则对应熵为H(X)=−(13log13+23log23)=log3−23log2<log2).

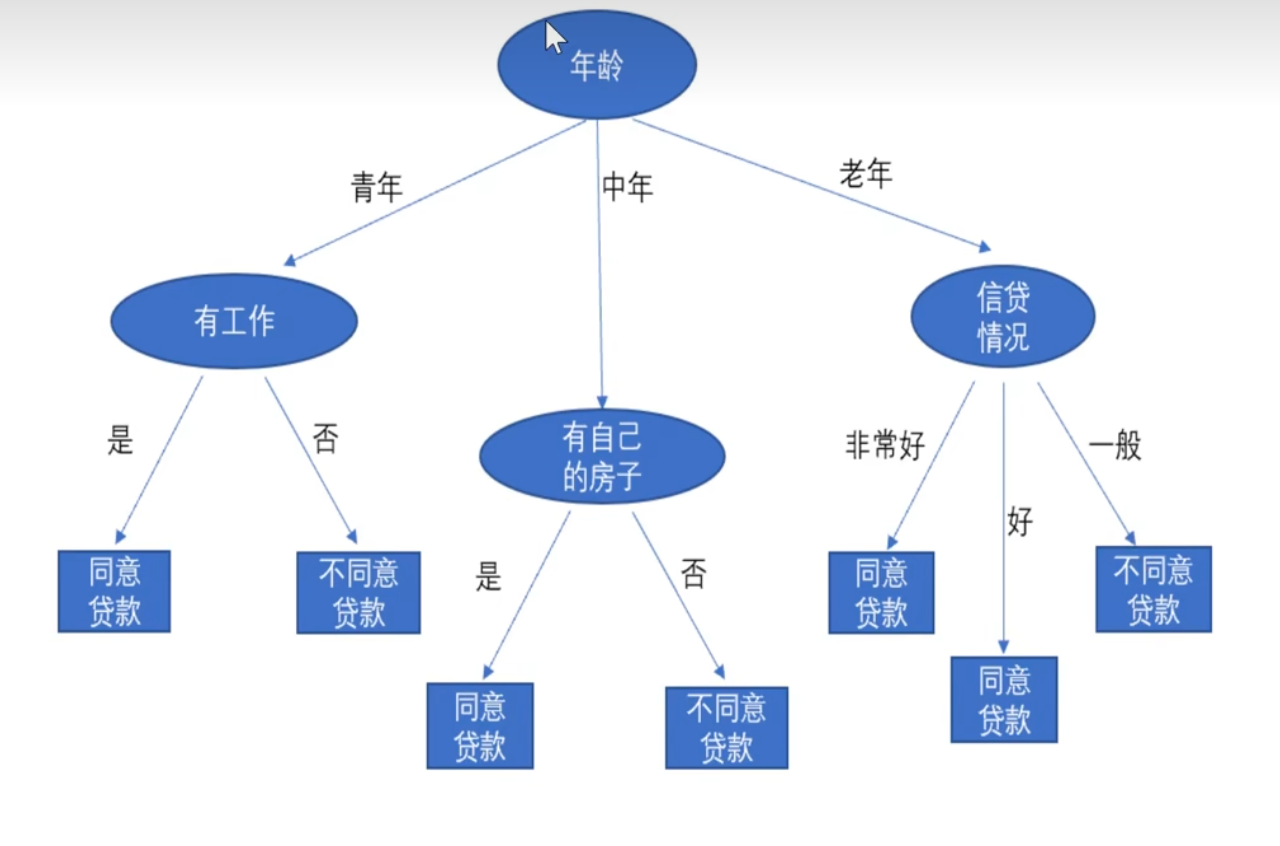
其中K表示类别,Ck表示属于第k类的个数。对于贷款申请样本数据表中得知,有两个类别(K=2),否(C1=6),是(C2=9),样本数15(D=15)
因此经验熵为:
经验条件熵:给定特征年龄A1后,所得到的小n个子集,每个子集计算其熵然后进行加权求和。给定年龄特征后,划分子集为3,因此n=3。例如,当i=1时,因此
等于
,下面计算
的经验熵,
,当i=2时,以此类推,
,
。因此,经验条件熵
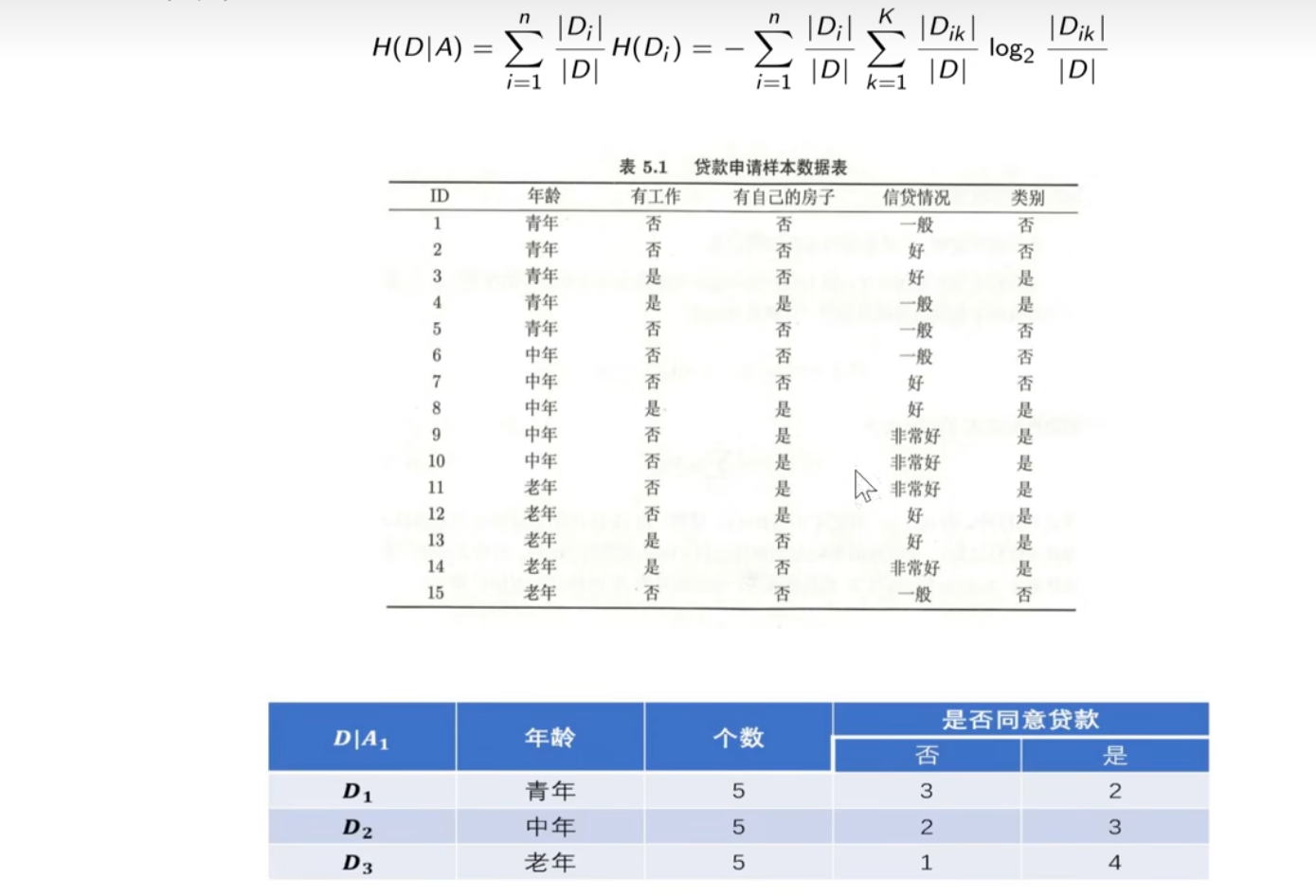
经验条件熵:给定特征工作A2后,划分子集为2,因此n=2。例如,当i=1时,因此
等于
,下面计算
的经验熵,
,当i=2时,
。因此,经验条件熵
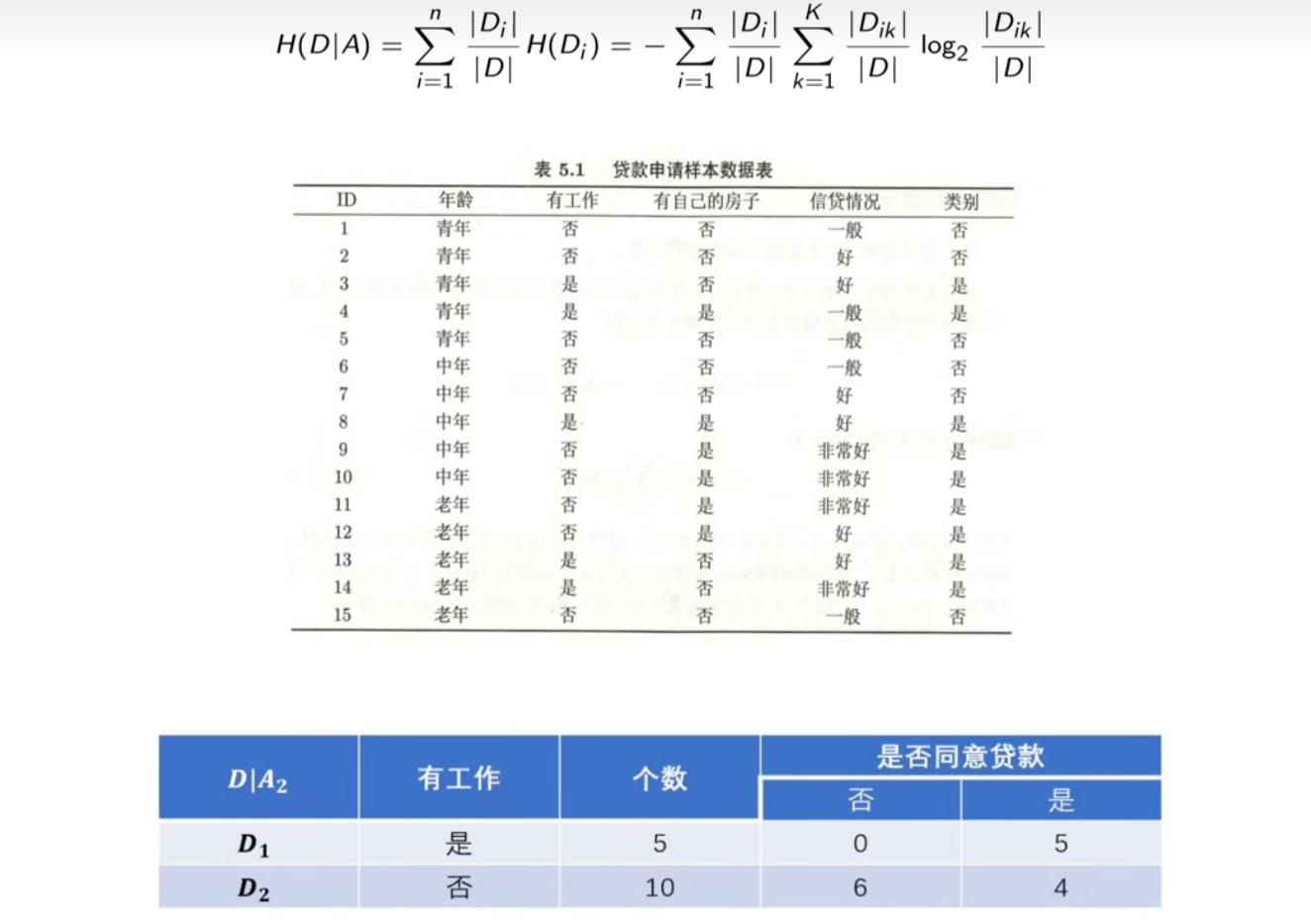
经验条件熵:给定特征房子A3后,划分子集为2,因此n=2。例如,当i=1时,因此
等于
,下面计算
的经验熵,
,当i=2时,
。因此,经验条件熵
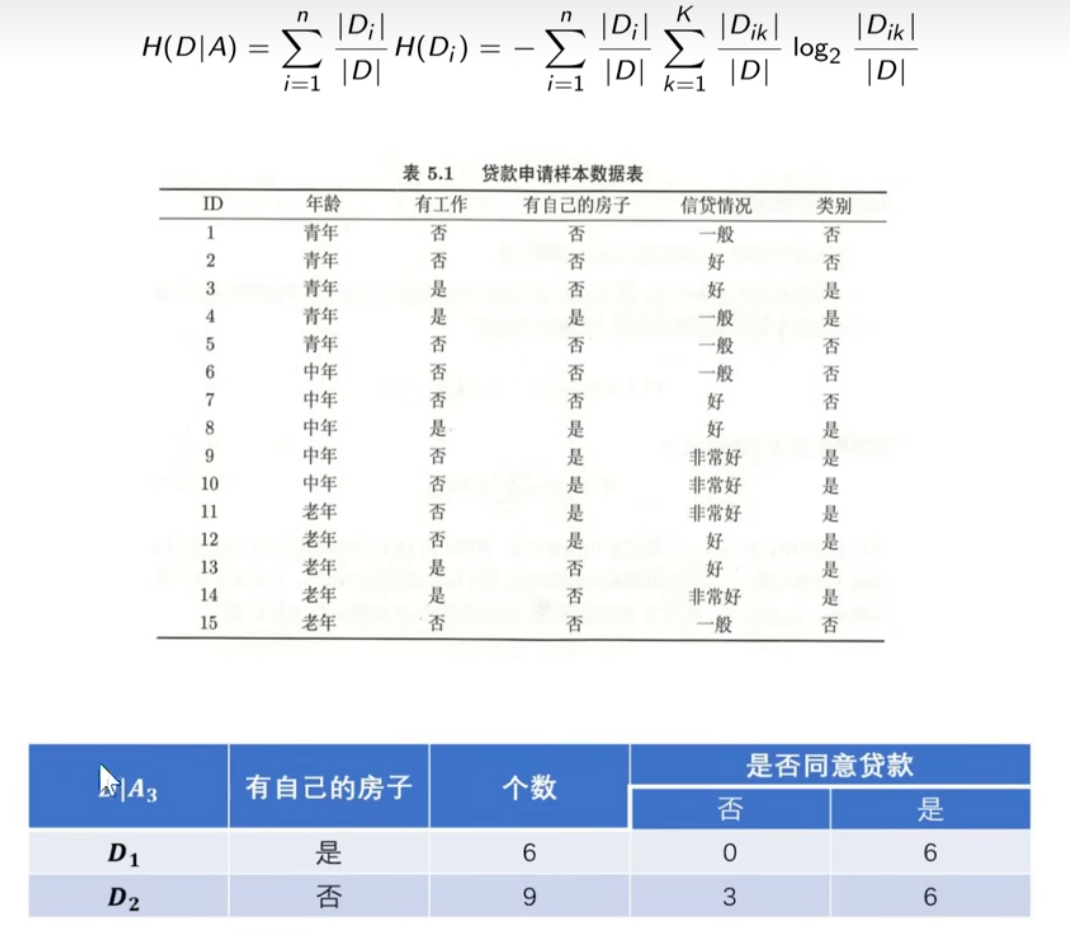
经验条件熵:给定特征信贷情况A4后,划分子集为3,因此n=3。例如,当i=1时,因此
等于
,下面计算
的经验熵,
,当i=2时,以此类推,
,
。因此,经验条件熵
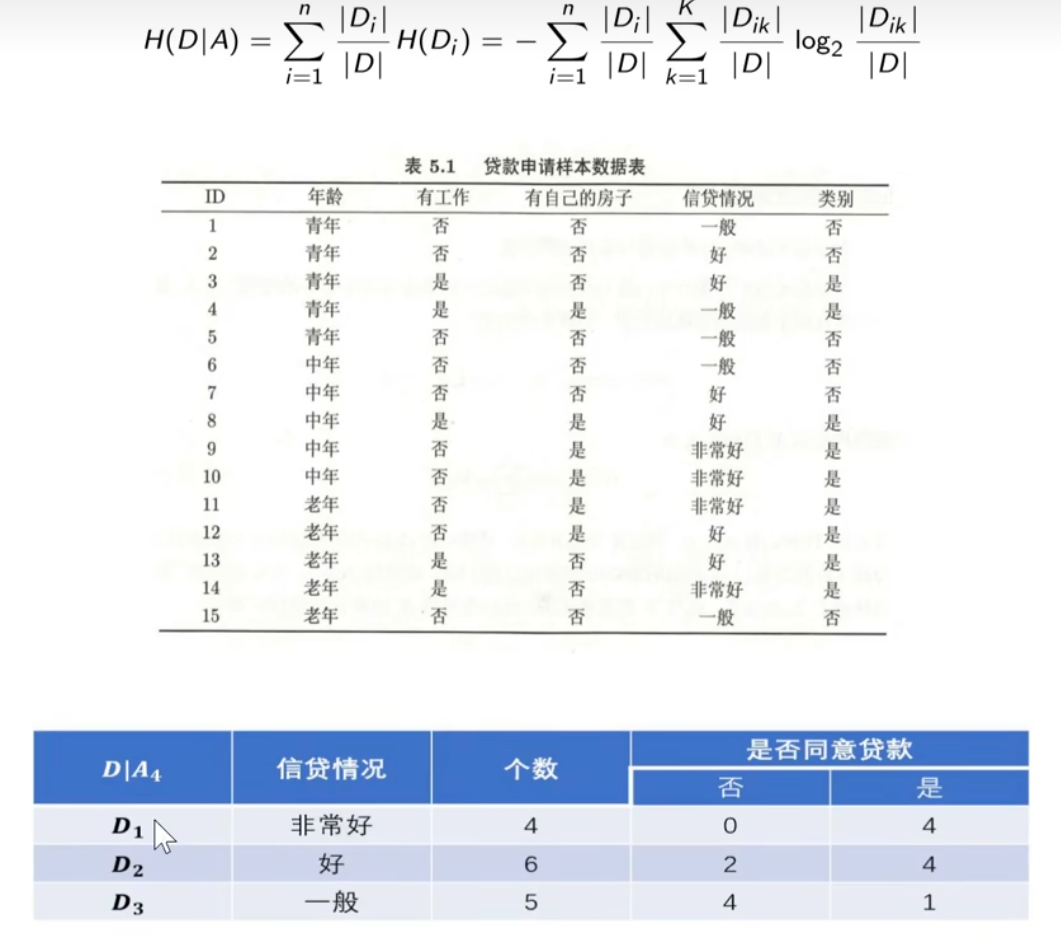
因此,信息增益就等于经验熵减去经验条件熵。对比下面四种不同特征的信息增益:
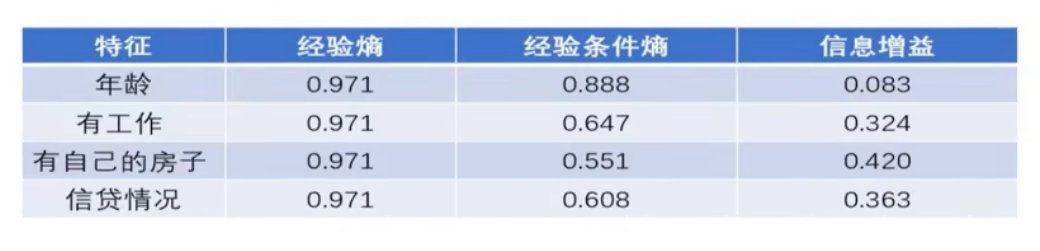
因此,信息增益最大的是有自己的房子,因此最优特征是有自己的房子。
3.2信息增益比
前面说到,信贷情况的特征有三个(一般,好,非常好),而特征有工作只有两种取值(是,否),因此特征信贷情况的信息增益可能大于特征有工作。而信贷情况的信息增益是0.363,有工作的信息增益是0.324,这个就可能是因为信贷情况的取值大于有工作的取值(3>2)。如何将取值较多的这个情况抵消掉呢?就要引入信息增益比。在信息增益的前提下,加入惩罚项。
信息增益比公式如下:
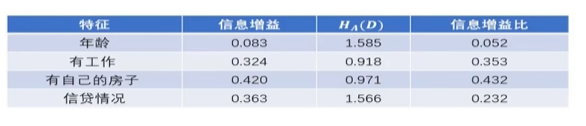
对比特征有工作和特征信贷情况,信息增益信贷情况大,但是特征有工作的信息增益比比特征信贷情况大。信息增益缺点趋向于特征取值较多的那个特征,信息增益比缺点趋向于特征取值较少的那个特征。具体选择哪一个需要结合实际情况。
