当前位置：首页 > news >正文

算法讲解--有效三角形的个数

news 2025/7/26 9:00:32

一,题目描述

给一个数组，判读该数组有多少个有效的三角形。

这里首先向讲解一下判断是否是三角形的方法：
1，三边的任意两边之和要大于第三边。

2，在有序的情况下，最小的两边大于第三边。

二,算法讲解

1，为什么要先排序后判断呢？

在题目解析中写到判断三条边能不能构成三角形的方法有两种：

第一种任意两边之后都要大于第三边，换句话说要想判断该三角形是不是三角形需要判断三次，而如果有序只需要判断一次。从时间复杂度的方面上讲，排序算法的时间复杂度是nlog^n，若是暴力求解需要三层循环时间复杂度是n^3。总体该解法的遍历部分是n^3。因此如果排序该解法的总体时间复杂度为n^3。而不排序需要3n^3。还是要远远慢于排序。

在下面讲的双指针法中也需要先对数值进行排序。因此不管哪一种方法，通过排序都可以使该算法时间更短。

在本题中，给的vector数据，可以直接使用C++标准库的sort进行排序。

2，暴力求解：

列出所有组成三角形的可能性，并且对每一种可能性进行是否是三角形进行判断。伪代码如下：

for(int i = 0; i < nums.size();i++){for(int j = i +1; j < nums.size();j++){for(int k = j +1; k < nums.size(); k++){if(nums[i]+nums[j] > nums[k]){sum++;}}}}

首先使用排序算法将目标数组排序。有序之后。使用三个for循环遍历出每一种组合的形式，如果可以构成三角形就把总数加加。

3，双指针法：

经过上面所讲的排序之后，该数组变成升序数组，现在随机给出一组数据如图：

定义一个sum变量来统计有效三角形的个数。

第一步：

在上文中讲到，在三个有序的数据中，只要较小的两个数的和大于第三个数就可以构成三角形。因此先确定最大的数如图为18 。第一个指针指向最小的数2 ，第二个指针指向次大的数14 。如图：

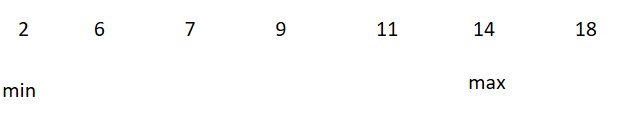
第二步：

此时得出2+14 < 18 。由此得出次大数都不能大于第三边，那么14之前的所有数据都不大于18，因此min++ 。如图：

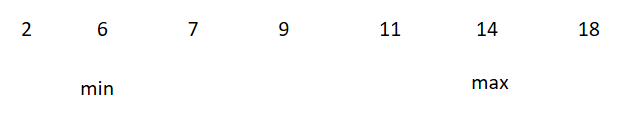
sum = sum + (max - min) = 5

第三步：

此时得出6 + 14 > 18。由此得出最小的数和14都可以大于18 。那么6和14这之间的所有数都可以满足大于18的条件。通过两个指针相减得出有效的三角形个数。之后max-- 。如图：

第四步：

此时 6 + 11 < 18 。重复第二步的操作。如图：

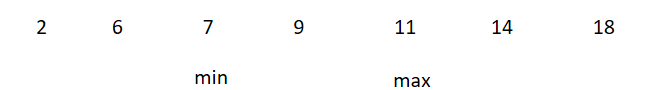
第五步：
此时 7 + 11 = 18 .。还是不能构成三角形。重复第二步的操作。如图：

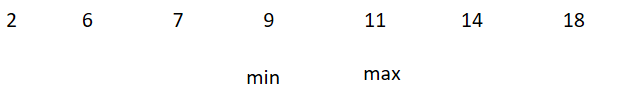
sum = sum +(max - min) = 6

第六步：

此时9 + 11 > 18 。max减减之后。两个指针相遇。说明当最大值为18所有能构成三角形的情况全部结束。现在使得最大值为14 。重复上面步骤。首先对每一个内部的个数相加。完成一个循环之后改变最大数的值。进行对内循环的数相加。直到最大数遍历结束。统计数目结束。

三,代码实现

int triangleNumber(vector<int>& nums) {int sum = 0;sort(nums.begin(),nums.end());for(int i = nums.size()-1; i > 1; i--){int min = 0;int max = i-1;while(min < max){if(nums[min] + nums[max] > nums[i]){sum = sum +max -min;max--;}else{min++;}}}return sum;}

当最大值为第三个数组时，该最大值已经是该数组最小的一组最大值，因此当i <= 1 时，循环结束。