当前位置： 首页 > news >正文

图的遍历：深度优先与广度优先

news 2025/7/26 7:44:11

图的遍历：深度优先与广度优先

大家好，今天我们来聊聊图遍历的两种经典算法：深度优先搜索（DFS）和广度优先搜索（BFS）。想象一下，你正在探索一个迷宫，有两种策略：一种是沿着一条路一直走到底，直到无路可走再回头（DFS）；另一种是同时探索所有可能的路径，一层一层向外扩展（BFS）。这两种策略各有优劣，适用于不同的场景。

在实际开发中，我们经常会遇到需要遍历图结构的场景，比如社交网络中的好友关系、网站页面之间的链接关系、文件系统的目录结构等。理解这两种遍历方式的原理和实现，对我们解决实际问题非常有帮助。

一、图的表示方法

在深入探讨遍历算法之前，我们先来看看如何在代码中表示图结构。图通常有两种表示方法：邻接矩阵和邻接表。

1. 邻接矩阵

邻接矩阵是一个二维数组，其中矩阵的行和列都代表图中的顶点。如果顶点i和顶点j之间有边相连，则矩阵中的matrix[i][j]值为1（或边的权重），否则为0。

// 无向图的邻接矩阵表示
const adjacencyMatrix = [[0, 1, 1, 0],  // 顶点0与顶点1、2相连[1, 0, 1, 1],  // 顶点1与顶点0、2、3相连[1, 1, 0, 0],  // 顶点2与顶点0、1相连[0, 1, 0, 0]   // 顶点3与顶点1相连
];

上述代码展示了一个简单的无向图的邻接矩阵表示。这种表示方法简单直观，但对于稀疏图（边数远小于顶点数平方的图）会浪费大量空间。

2. 邻接表

邻接表使用一个数组来存储所有顶点，每个顶点对应一个链表，链表中存储与该顶点相连的其他顶点。

// 邻接表表示
const adjacencyList = [[1, 2],    // 顶点0的邻居：顶点1、2[0, 2, 3], // 顶点1的邻居：顶点0、2、3[0, 1],    // 顶点2的邻居：顶点0、1[1]        // 顶点3的邻居：顶点1
];

邻接表更适合表示稀疏图，节省空间，且能快速找到一个顶点的所有邻居。在本文中，我们将主要使用邻接表来表示图。

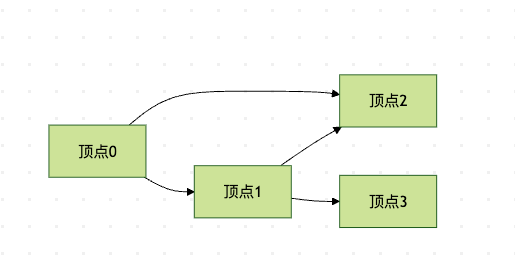
图1：示例图结构

二、深度优先搜索（DFS）

理解了图的表示方法后，我们来看第一种遍历算法：深度优先搜索。DFS就像走迷宫时选择一条路一直走到底，直到无路可走再回头尝试其他路径。

1. DFS的基本思想

DFS从起始顶点开始，沿着一条路径尽可能深入地访问顶点，直到这条路径上的所有顶点都被访问过，然后回溯到前一个顶点，继续探索其他未被访问的路径。

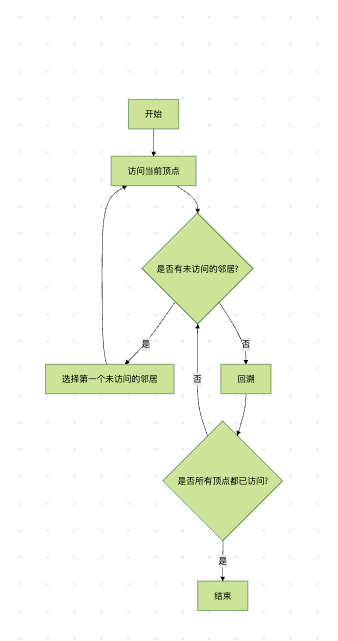
图2：DFS算法流程图

2. DFS的递归实现

DFS可以用递归的方式简洁地实现：

function dfs(graph, start) {const visited = new Set(); // 记录已访问的顶点function traverse(node) {if (visited.has(node)) return;console.log(`访问顶点: ${node}`);visited.add(node);for (const neighbor of graph[node]) {traverse(neighbor);}}traverse(start);
}// 使用示例
const graph = [[1, 2],    // 顶点0[0, 2, 3], // 顶点1[0, 1],    // 顶点2[1]        // 顶点3
];dfs(graph, 0); // 从顶点0开始DFS遍历

上述代码展示了DFS的递归实现。我们使用一个Set来记录已经访问过的顶点，避免重复访问。对于每个顶点，我们先访问它，然后递归访问它的所有邻居。

3. DFS的迭代实现

虽然递归实现简洁，但对于深度很大的图可能会导致栈溢出。我们可以使用显式的栈结构来实现迭代版本的DFS：

function dfsIterative(graph, start) {const stack = [start];       // 使用栈来模拟递归const visited = new Set();   // 记录已访问的顶点while (stack.length > 0) {const node = stack.pop(); // 取出栈顶元素if (visited.has(node)) continue;console.log(`访问顶点: ${node}`);visited.add(node);// 将邻居逆序压入栈中，保证访问顺序与递归一致for (let i = graph[node].length - 1; i >= 0; i--) {const neighbor = graph[node][i];if (!visited.has(neighbor)) {stack.push(neighbor);}}}
}

迭代版本的DFS使用栈来模拟递归调用。注意我们需要将邻居逆序压入栈中，这样才能保证访问顺序与递归实现一致。

4. DFS的应用场景

DFS适用于以下场景：

  • 拓扑排序
  • 检测图中的环
  • 寻找连通分量
  • 解决迷宫问题
  • 生成迷宫

小贴士： DFS通常使用栈（递归调用栈或显式栈）来实现，它的空间复杂度主要取决于图的深度，在最坏情况下（如线性链表）为O(V)，其中V是顶点数。

三、广度优先搜索（BFS）

理解了DFS后，我们来看另一种遍历方式：广度优先搜索。BFS就像水波扩散一样，从起点开始一层一层向外扩展，先访问离起点近的顶点，再访问离起点远的顶点。

1. BFS的基本思想

BFS从起始顶点开始，先访问所有与起始顶点直接相连的顶点（第一层），然后访问这些顶点的邻居（第二层），依此类推，直到所有顶点都被访问。

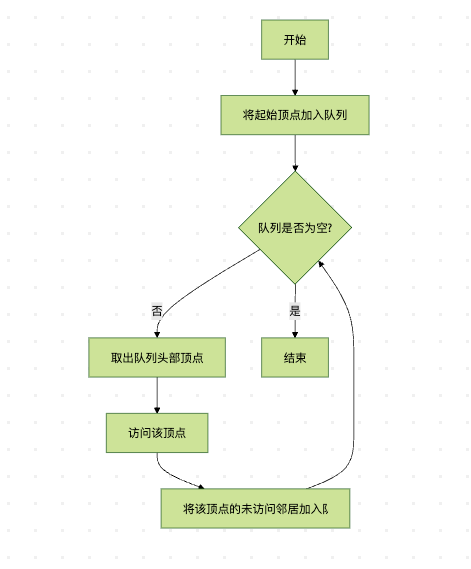
图3：BFS算法流程图

2. BFS的实现

BFS通常使用队列来实现：

function bfs(graph, start) {const queue = [start];      // 使用队列来管理待访问顶点const visited = new Set();  // 记录已访问的顶点visited.add(start);while (queue.length > 0) {const node = queue.shift(); // 取出队列头部顶点console.log(`访问顶点: ${node}`);// 将未访问的邻居加入队列for (const neighbor of graph[node]) {if (!visited.has(neighbor)) {visited.add(neighbor);queue.push(neighbor);}}}
}

BFS的实现使用队列来管理待访问的顶点。我们首先将起始顶点加入队列，然后不断从队列中取出顶点进行访问，并将其未访问的邻居加入队列尾部。

3. BFS的应用场景

BFS适用于以下场景：

  • 寻找最短路径（无权图）
  • 社交网络中的好友推荐（寻找二度、三度好友）
  • 网络爬虫的页面抓取策略
  • 广播网络中的信息传播
  • 解决迷宫的最短路径问题

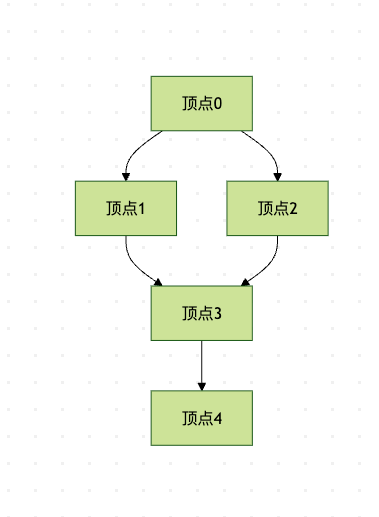
图4：BFS遍历顺序示例

小贴士： BFS的空间复杂度在最坏情况下是O(V)，因为可能需要存储所有顶点。对于连通图，BFS能找到从起点到其他所有顶点的最短路径（边数最少）。

四、DFS与BFS的比较

现在我们已经了解了两种遍历算法，让我们来比较它们的异同点：

比较项DFSBFS
数据结构栈（递归或显式）队列
空间复杂度O(深度)，最坏O(V)O(宽度)，最坏O(V)
时间复杂度O(V+E)O(V+E)
适用场景拓扑排序、检测环、连通分量最短路径、层级遍历
遍历顺序深度优先广度优先

五、实际应用案例

让我们通过一个实际案例来看看如何选择使用DFS还是BFS。假设我们需要在一个社交网络中找出两个人之间的最短连接路径（最少中间人）。

1. 问题分析

这是一个典型的最短路径问题，BFS是更合适的选择，因为它能保证找到边数最少的路径。而DFS可能会找到一条路径，但不一定是最短的。

2. 解决方案实现

function findShortestPath(graph, start, end) {const queue = [[start]];      // 存储路径的队列const visited = new Set();    // 记录已访问的顶点visited.add(start);while (queue.length > 0) {const path = queue.shift();  // 取出第一条路径const node = path[path.length - 1]; // 路径的最后一个顶点// 如果到达目标顶点，返回路径if (node === end) {return path;}// 遍历邻居for (const neighbor of graph[node]) {if (!visited.has(neighbor)) {visited.add(neighbor);// 创建新路径并加入队列const newPath = [...path, neighbor];queue.push(newPath);}}}return null; // 没有找到路径
}// 使用示例
const socialNetwork = [[1, 2],    // 用户0的朋友：1, 2[0, 3, 4], // 用户1的朋友：0, 3, 4[0, 3],    // 用户2的朋友：0, 3[1, 2, 5], // 用户3的朋友：1, 2, 5[1],       // 用户4的朋友：1[3]        // 用户5的朋友：3
];console.log(findShortestPath(socialNetwork, 0, 5)); // [0, 1, 3, 5] 或 [0, 2, 3, 5]

这段代码使用BFS来寻找两个用户之间的最短连接路径。我们不仅记录访问过的顶点，还记录从起点到当前顶点的完整路径。当找到目标顶点时，返回这条路径，这就是最短路径。

注意： 如果图是加权的（边有权重），BFS就不能直接用于寻找最短路径了，这时需要使用Dijkstra算法或A*算法等更复杂的算法。

六、总结

通过今天的讨论，我们深入了解了图的两种基本遍历算法：深度优先搜索（DFS）和广度优先搜索（BFS）。让我们回顾一下主要内容：

  1. 图的表示方法：我们学习了邻接矩阵和邻接表两种表示方法，并了解了它们的优缺点。
  2. 深度优先搜索（DFS）：我们探讨了DFS的递归和迭代实现，了解了它的应用场景和特点。
  3. 广度优先搜索（BFS）：我们学习了BFS的队列实现，并理解了它在寻找最短路径等方面的优势。
  4. 算法比较：我们对比了DFS和BFS在数据结构、空间复杂度、时间复杂度和适用场景等方面的差异。
  5. 实际应用：我们通过社交网络中的最短路径问题，展示了如何在实际问题中选择合适的遍历算法。

理解这两种遍历算法是学习更复杂图算法的基础。在实际开发中，我们需要根据具体问题的需求选择合适的算法。DFS更适合需要深入探索的场景，而BFS则适合需要广度扩展或寻找最短路径的场景。

希望大家通过这篇文章对图的遍历有了更深入的理解。如果有任何问题或想法，欢迎随时交流讨论。让我们共同进步，探索算法的美妙世界！

http://www.dtcms.com/a/297896.html

相关文章：

  • SpringBoot学习路径二--Spring Boot自动配置原理深度解析
  • Qt 状态机框架：复杂交互逻辑的处理
  • R 语言绘制六种精美热图：转录组数据可视化实践（基于 pheatmap 包）
  • 从零开始学习Dify-数据库数据可视化(五)
  • java的设计模式及代理模式
  • 负载均衡：提升业务性能的关键技术
  • Zabbix告警系统集成指南：从钉钉机器人到网易邮件的全流程配置
  • pytest-html 优势及与其他插件对比
  • 自动驾驶领域中的Python机器学习
  • VLA：自动驾驶的“新大脑”？
  • npm init vite-app runoob-vue3-test2 ，npm init vue@latest，指令区别
  • C语言第 9 天学习笔记：数组（二维数组与字符数组）
  • Java-Properties类和properties文件详解
  • 同声传译新突破！字节跳动发布 Seed LiveInterpret 2.0
  • 深入探索嵌入式仿真教学：以酒精测试仪实验为例的高效学习实践
  • C++常见面试题之一
  • win11平台上mysql 数据库迁移
  • 【C#补全计划：类和对象（七）—— 重写虚方法】
  • CMOS知识点 双阱工艺 三阱工艺
  • 大数据中心——解读60页IDC云数据中心机房运维服务解决方案【附全文阅读】
  • 【优选算法】链表
  • 2025.7.25 测试 总结
  • C/C++---I/O性能优化
  • ISAAC ROS 在Jetson Orin NX上的部署
  • 自动化UI测试工具TestComplete的AI双引擎：即时数据集 + 自愈测试
  • BGP负载均衡-9
  • C#观察者模式示例代码
  • Qt 拔网线等情况下收不到disconnected()信号
  • 数据结构之 【排序】(非递归实现快速排序)
  • 【Web安全】逻辑漏洞之URL跳转漏洞：原理、场景与防御