线段树学习笔记 - 练习题(2)
文章目录
- 1. 前言
- 2. P3870 [TJOI2009] 开关
- 3. P2184 贪婪大陆
- 4. P1438 无聊的数列
- 5. P1471 方差
1. 前言
线段树系列文章:
- 线段树学习笔记。
- 线段树学习笔记 - 练习题(1)。
前一篇做了几道线段树的题目,这篇文章就继续看下线段树的相关题目,还是一样,学习视频:算法讲解112【扩展】线段树专题3-线段树维护更多类型的信息,题目都是左神视频上的,思路也可以看这个视频。
2. P3870 [TJOI2009] 开关
P3870 [TJOI2009] 开关。
题目描述
现有 nnn 盏灯排成一排,从左到右依次编号为:111,222,……,nnn。然后依次执行 mmm 项操作。
操作分为两种:
- 指定一个区间 [a,b][a,b][a,b],然后改变编号在这个区间内的灯的状态(把开着的灯关上,关着的灯打开);
- 指定一个区间 [a,b][a,b][a,b],要求你输出这个区间内有多少盏灯是打开的。
灯在初始时都是关着的。
输入格式
第一行有两个整数 nnn 和 mmm,分别表示灯的数目和操作的数目。
接下来有 mmm 行,每行有三个整数,依次为:ccc、aaa、bbb。其中 ccc 表示操作的种类。
- 当 ccc 的值为 000 时,表示是第一种操作。
- 当 ccc 的值为 111 时,表示是第二种操作。
aaa 和 bbb 则分别表示了操作区间的左右边界。
输出格式
每当遇到第二种操作时,输出一行,包含一个整数,表示此时在查询的区间中打开的灯的数目。
输入输出样例 #1
输入 #1
4 5
0 1 2
0 2 4
1 2 3
0 2 4
1 1 4
输出 #1
1
2
说明/提示
数据规模与约定
对于全部的测试点,保证 2≤n≤1052\le n\le 10^52≤n≤105,1≤m≤1051\le m\le 10^51≤m≤105,1≤a,b≤n1\le a,b\le n1≤a,b≤n,c∈{0,1}c\in\{0,1\}c∈{0,1}。
思路:
这道题就是范围重置和范围查询,初始值为 0 表示灯是关上的,1 表示灯打开了,其实就是范围重置维护累加和,那么如果到了一个范围能不能在 O(1) 时间内懒更新完这个范围的累加和呢?答案是可以的,比如这个范围长度是 n,假设现在 light[i] = m,那么翻转过后 light[i] = n - m,所以是可以 O(1) 时间懒更新的,下面看下 code。
import java.io.*;public class Main {public static int MAXN = 100001;public static int[] light = new int[MAXN << 2];// 懒更新数组, 如果为 true 就表示这个范围内的值要翻转了public static boolean[] reverse = new boolean[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;in.nextToken();int m = (int) in.nval;build(1, n, 1);for (int i = 1, op, jobl, jobr; i <= m; i++) {in.nextToken();op = (int) in.nval;in.nextToken();jobl = (int) in.nval;in.nextToken();jobr = (int) in.nval;if (op == 0) {reverse(jobl, jobr, 1, n, 1);} else {out.println(query(jobl, jobr, 1, n, 1));}}out.flush();out.close();br.close();}private static int query(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return light[i];} else {int ans = 0;int mid = l + ((r - l) >> 1);down(i, mid - l + 1, r - mid);if (jobl <= mid) {ans += query(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += query(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}}private static void reverse(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {lazy(i, r - l + 1);} else {int mid = l + ((r - l) >> 1);down(i, mid - l + 1, r - mid);if (jobl <= mid) {reverse(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {reverse(jobl, jobr, mid + 1, r, i << 1 | 1);}up(i);}}private static void down(int i, int ln, int rn) {if (reverse[i]) {lazy(i << 1, ln);lazy(i << 1 | 1, rn);reverse[i] = false;}}private static void lazy(int i, int n) {light[i] = n - light[i];// 假设子数组是 true, 那么再次翻转就是 !reverse[i]// 不能直接设置为 falsereverse[i] = !reverse[i];}private static void build(int l, int r, int i) {if (l == r) {light[i] = 0;} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}reverse[i] = false;}private static void up(int i) {light[i] = light[i << 1] + light[i << 1 | 1];}
}
3. P2184 贪婪大陆
P2184 贪婪大陆。
题目背景
面对蚂蚁们的疯狂进攻,小 FF 的 Tower defence 宣告失败……人类被蚂蚁们逼到了 Greed Island 上的一个海湾。现在,小 FF 的后方是一望无际的大海,前方是变异了的超级蚂蚁。小 FF 还有大好前程,他可不想命丧于此, 于是他派遣手下最后一批改造 SCV 布置地雷以阻挡蚂蚁们的进攻。
题目描述
小 FF 最后一道防线是一条长度为 nnn 的战壕,小 FF 拥有无数多种地雷,而 SCV 每次可以在 [L,R][L, R][L,R] 区间埋放同一种不同于之前已经埋放的地雷。由于情况已经十万火急,小 FF 在某些时候可能会询问你在 [L′,R′][L',R'][L′,R′] 区间内有多少种不同的地雷,他希望你能尽快的给予答复。
输入格式
第一行为两个整数 nnn 和 mmm,nnn 表示防线长度,mmm 表示 SCV 布雷次数及小 FF 询问的次数总和。
接下来有 mmm 行,每行三个整数 q,l,rq,l,rq,l,r:
- 若 q=1q=1q=1,则表示 SCV 在 [l,r][l, r][l,r] 这段区间布上一种地雷;
- 若 q=2q=2q=2,则表示小 FF 询问当前 [l,r][l, r][l,r] 区间总共有多少种地雷。
输出格式
对于小 FF 的每次询问,输出一个答案(单独一行),表示当前区间地雷总数。
输入输出样例 #1
输入 #1
5 4
1 1 3
2 2 5
1 2 4
2 3 5
输出 #1
1
2
说明/提示
数据规模与约定
- 对于 30%30\%30% 的数据,0≤n0 \le n0≤n,m≤1000m \le 1000m≤1000。
- 对于 100%100\%100% 的数据,0≤n0 \le n0≤n,m≤105m \le 10^5m≤105。
思路:
这道题就是两个操作,放地雷和查地雷数,注意这里就不是范围更新了,比如 [1,4] 区间现在放了地雷 1,[3,6] 区间放了地雷 2,那么最终 [3,4] 区间地雷数就是 2,也就是说地雷数是叠加的,而不是被覆盖的关系。
那么能不能每一次都区间 + 1 然后维护最大值呢,这样是可以表示这个区间的地雷数,但是最后查询的时候还是没办法查出来总的地雷数。还是上面的例子,比如 [1,4] 区间现在放了地雷 1,[3,6] 区间放了地雷 2,[2,2] 区间放了地雷 3,最终结果如下。
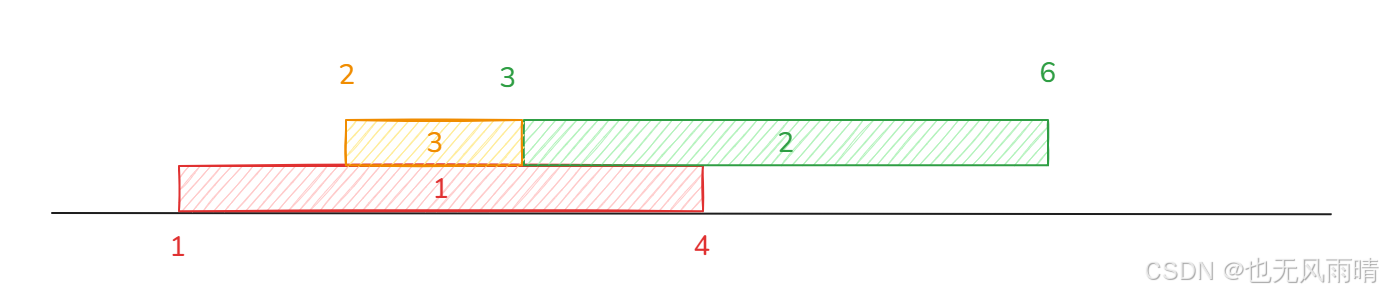
然后我们要查询 [1,6] 范围的地雷数,结果是 3,但是如果维护的最大值,那最大值就是 2,也就是 [2,4] 这个区间的最大值是 2,但是根据这个最大值是没办法算出总地雷数的,所以得另外想个办法,既然维护整个区间是不行的,那么能不能维护左右边界来求地雷总数呢,我们可以用 left 和 right 两个数组来维护地雷的左右边界,left[i] 表示这个范围的地雷左边界总数,right[i] 表示这个范围的地雷右边界总数,更新的时候不用范围更新了,因为就算是范围更新也是 [l,l] 更新和 [r,r] 更新,也就是单点更新了,所以直接深入到叶子节点去更新,然后再维护累加和,整体时间复杂度是 O(n∗log2n)O(n * log_{2}{n})O(n∗log2n)。
那么查询要如何查询呢,来看下下面的图。
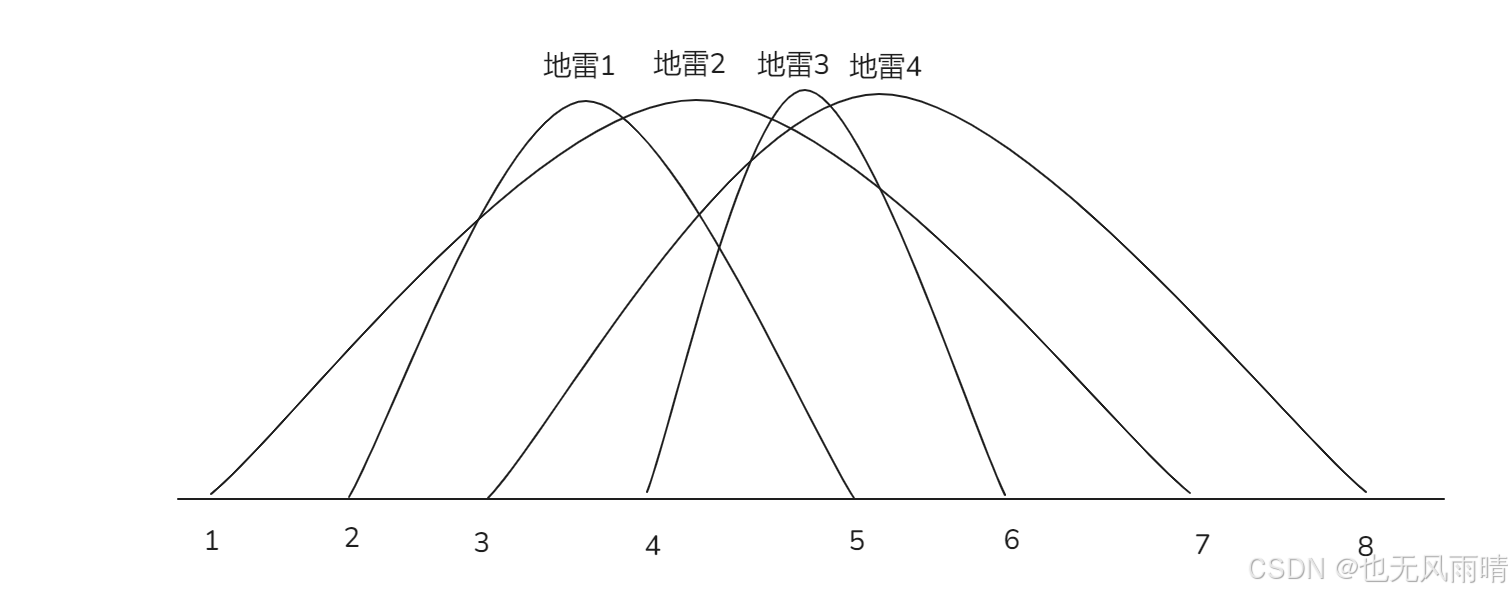
上面图一共埋了 4 个地雷,范围是从 1-8,比如我们要求 [3,7] 这个范围内一共有多少地雷,首先求出来 [1,r] 这个范围包含了多少个地雷的左边界,然后再求出 [1,2] 包含了多少地雷的右边界,一相减就求出结果了,总结来说就是加入 [l,r] 范围先求出 [1,r] 范围有多少地雷的左边界,然后求出 [1,l - 1] 范围有多少地雷的右边界,再相减。
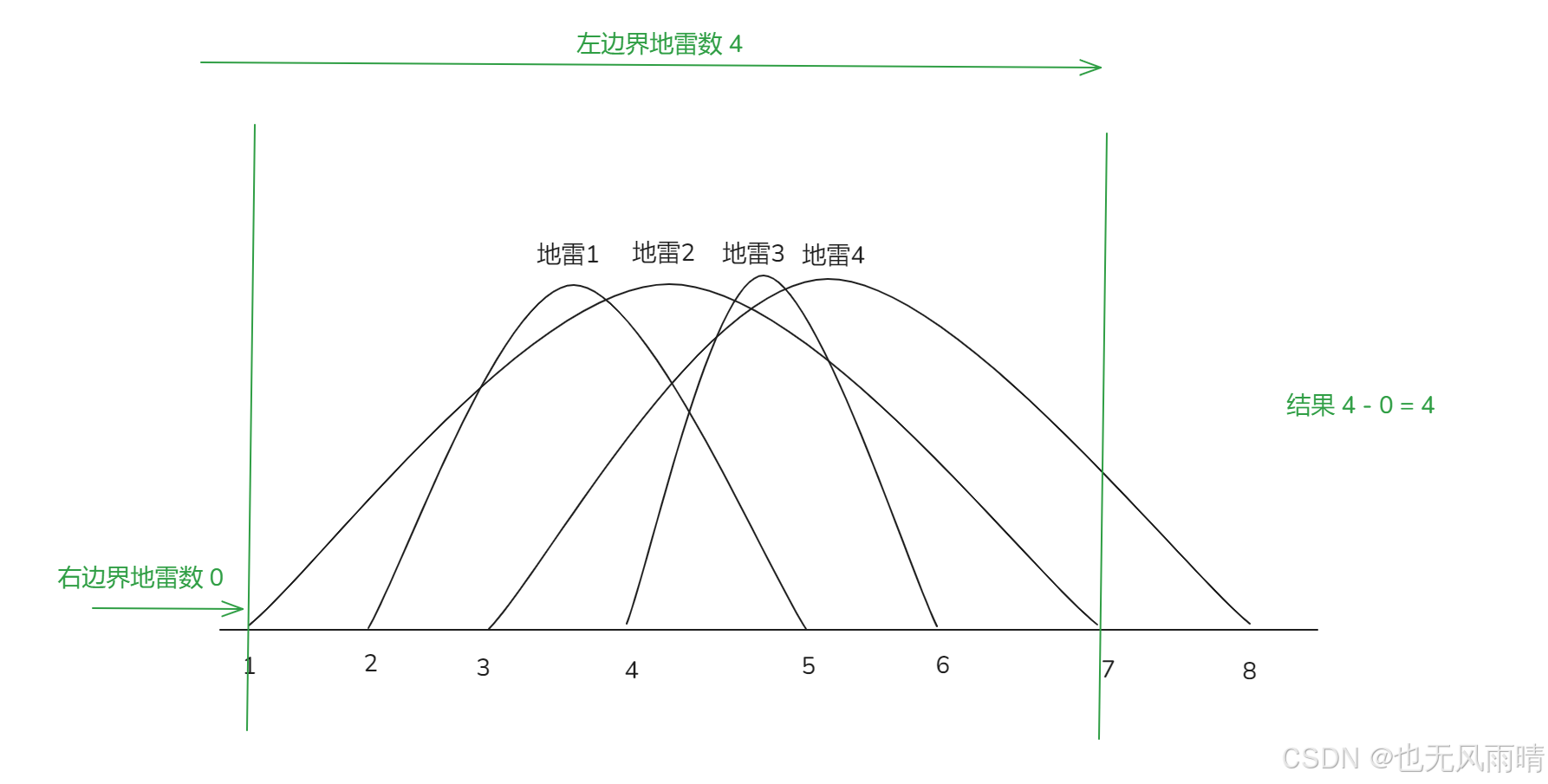
这样求出来的结果是 4,那么为什么可以这么求,首先要明确什么地雷会落在 [l,r] 范围。
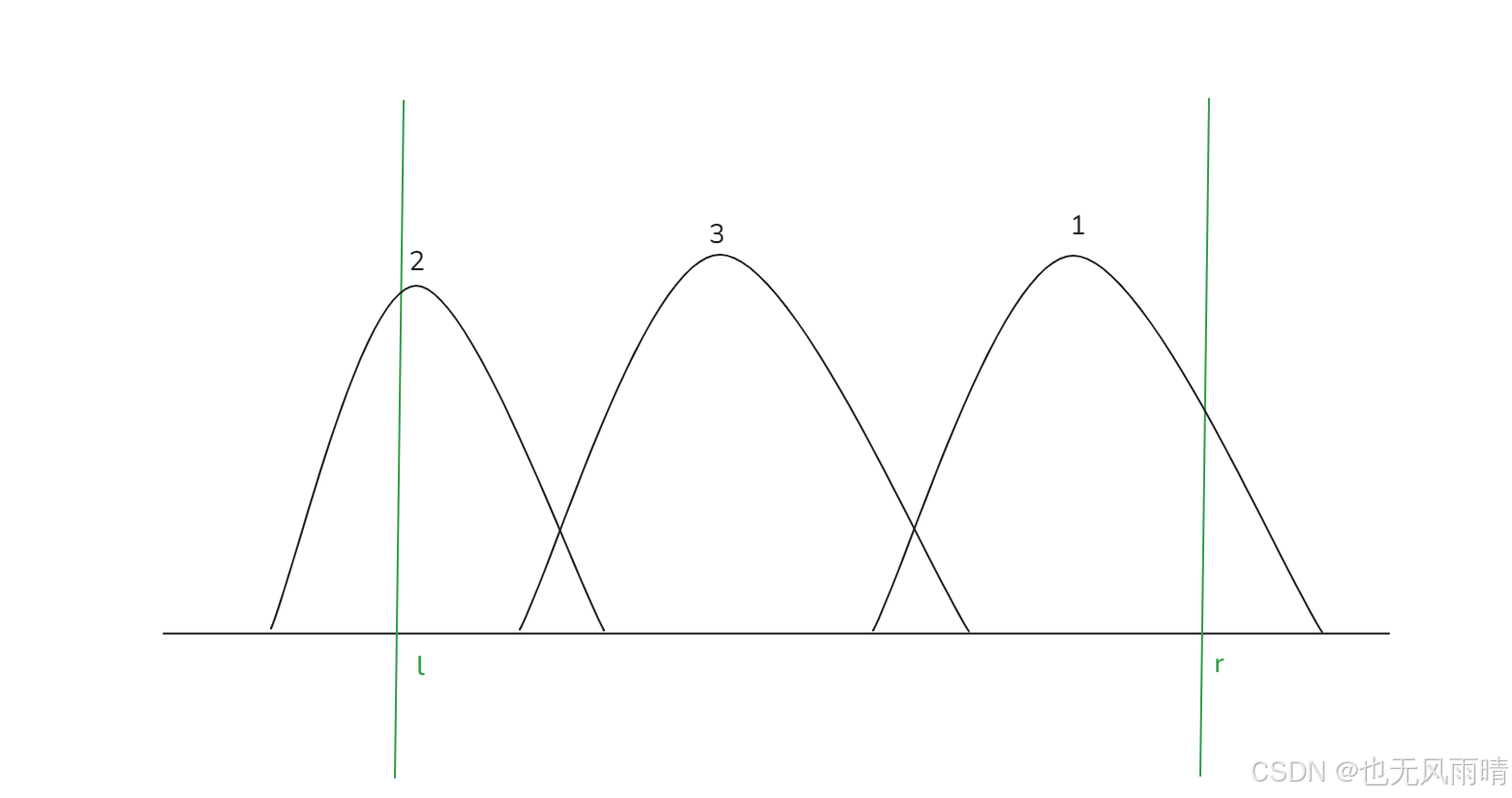
可以看到,这两种可以就可以概括了,就是下面两种:
- 左边界 < l,右边界 >= l
- l < 左边界 < r
所以可以看到,汇总以下,最终要落在 [l,r] 范围的地雷左边界肯定是要 <= r 的,于是第一步就是求出 [1,r] 这个范围的有多少个地雷的左边界,然后右边界肯定是不能小于 l 的,如果小于 l 就落不到这个区间了,所以求出来右边界 <= l - 1 的地雷数,然后相减就行了,下面看下 code。
import java.io.*;public class Main {public static int MAXN = 100001;public static int[] left = new int[MAXN << 2];public static int[] right = new int[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;in.nextToken();int m = (int) in.nval;build(1, n, 1);for (int i = 1; i <= m; i++) {in.nextToken();int op = (int) in.nval;in.nextToken();int jobl = (int) in.nval;in.nextToken();int jobr = (int) in.nval;if (op == 1) {add(0, jobl, 1, n, 1);add(1, jobr, 1, n, 1);} else {// [1, r] 的左边界 - [1, l-1] 的右边界地雷数int cl = query(0, 1, jobr, 1, n, 1);int cr = jobl == 1 ? 0 : query(1, 1, jobl - 1, 1, n, 1);out.println(cl - cr);}}out.flush();out.close();br.close();}public static int query(int type, int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return type == 0 ? left[i] : right[i];}int res = 0;int mid = l + ((r - l) >> 1);if (jobl <= mid) {res += query(type, jobl, jobr, l, mid, i << 1);}if (jobr > mid) {res += query(type, jobl, jobr, mid + 1, r, i << 1 | 1);}return res;}public static void add(int type, int jobi, int l, int r, int i) {// 更新直接到叶子节点更新,不需要懒更新了,数据量不大if (l == r) {if (type == 0) {left[i]++;} else {right[i]++;}} else {int mid = l + ((r - l) >> 1);if (jobi <= mid) {add(type, jobi, l, mid, i << 1);}if (jobi > mid) {add(type, jobi, mid + 1, r, i << 1 | 1);}up(i);}}private static void up(int i) {left[i] = left[i << 1] + left[i << 1 | 1];right[i] = right[i << 1] + right[i << 1 | 1];}private static void build(int l, int r, int i) {if (l == r) {left[i] = right[i] = 0;} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);}}}
4. P1438 无聊的数列
P1438 无聊的数列
题目背景
无聊的 YYB 总喜欢搞出一些正常人无法搞出的东西。有一天,无聊的 YYB 想出了一道无聊的题:无聊的数列。。。
题目描述
维护一个数列 aia_iai,支持两种操作:
-
1 l r K D:给出一个长度等于 r−l+1r-l+1r−l+1 的等差数列,首项为 KKK,公差为 DDD,并将它对应加到 [l,r][l,r][l,r] 范围中的每一个数上。即:令 al=al+K,al+1=al+1+K+D…ar=ar+K+(r−l)×Da_l=a_l+K,a_{l+1}=a_{l+1}+K+D\ldots a_r=a_r+K+(r-l) \times Dal=al+K,al+1=al+1+K+D…ar=ar+K+(r−l)×D。 -
2 p:询问序列的第 ppp 个数的值 apa_pap。
输入格式
第一行两个整数数 n,mn,mn,m 表示数列长度和操作个数。
第二行 nnn 个整数,第 iii 个数表示 aia_iai。
接下来的 mmm 行,每行先输入一个整数 optoptopt。
若 opt=1opt=1opt=1 则再输入四个整数 lrKDl\ r\ K\ Dl r K D;
若 opt=2opt=2opt=2 则再输入一个整数 ppp。
输出格式
对于每个询问,一行一个整数表示答案。
输入输出样例 #1
输入 #1
5 2
1 2 3 4 5
1 2 4 1 2
2 3
输出 #1
6
说明/提示
数据规模与约定
对于 100%100\%100% 数据,0≤n,m≤105,−200≤ai,K,D≤200,1≤l≤r≤n,1≤p≤n0\le n,m \le 10^5,-200\le a_i,K,D\le 200, 1 \leq l \leq r \leq n, 1 \leq p \leq n0≤n,m≤105,−200≤ai,K,D≤200,1≤l≤r≤n,1≤p≤n。
思路:
这个就是要加一个等差数列,而且比较特殊的一点就是这里第 2 个操作不是范围查询,只是单点查询,因此这里可以对差分数组构造线段树,那么对于第一个操作,首项为 k,公差为 d 的等差数列,假设 k = 2,d = 3,假设 l = 2,r = 5,那么添加的等差数列就是 2,2 + 3,2 + 3 * 2, 2 + 33,2 + 34。
对于线段树维护差分数组的范围增加还是比较容易的,首先就是在 [2,2] 的位置 + 2,然后在 [3,5] 范围 + 3,最后别忘了在 6 位置减去总和,也就是减去 2 + (3 * 4),这是差分数组的性质决定的,比如要在原数组 [l,r] 范围 + v,那么对于差分数组的修改就是 d[l] + v,d[r + 1] - v,这样求前缀和的时候求出来原数组的 [l,r] 范围就都是 v 了,对于线段数也是,由于差分数组这个范围增加到 r 这个区间一共加了 2 + (3 * 4),因此 r + 1 位置减去 2 + (3 * 4) 抵消影响,这样线段树 query 求 [1,p] 的范围总和就是下标 p 的原数组值了。
import java.io.*;public class Main {public static int MAXN = 100001;public static long[] diff = new long[MAXN];public static long[] sum = new long[MAXN << 2];public static long[] add = new long[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;in.nextToken();int m = (int) in.nval;int pre = 0, cur = 0;for (int i = 1; i <= n; i++) {in.nextToken();cur = (int) in.nval;diff[i] = cur - pre;pre = cur;}build(1, n, 1);for (int i = 1; i <= m; i++) {in.nextToken();int op = (int) in.nval;if (op == 1) {in.nextToken();int jobl = (int) in.nval;in.nextToken();int jobr = (int) in.nval;in.nextToken();long k = (long) in.nval;in.nextToken();long d = (long) in.nval;long e = k + d * (jobr - jobl);add(jobl, jobl, k, 1, n, 1);if (jobl < jobr) {add(jobl + 1, jobr, d, 1, n, 1);}if (jobr + 1 <= n) {add(jobr + 1, jobr + 1, -e, 1, n, 1);}} else {in.nextToken();int p = (int) in.nval;out.println(query(1, p, 1, n, 1));}}out.flush();out.close();br.close();}private static long query(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];}long ans = 0;int mid = l + ((r - l) >> 1);down(i, mid - l + 1, r - mid);if (jobl <= mid) {ans += query(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += query(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}private static void build(int l, int r, int i) {if (l == r) {sum[i] = diff[l];} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}add[i] = 0;}private static void up(int i) {sum[i] = sum[i << 1] + sum[i << 1 | 1];}public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {lazy(i, jobv, r - l + 1);} else {int mid = l + ((r - l) >> 1);down(i, mid - l + 1, r - mid);if (jobl <= mid) {add(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {add(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}private static void down(int i, int ln, int rn) {if (add[i] != 0) {lazy(i << 1, add[i], ln);lazy(i << 1 | 1, add[i], rn);add[i] = 0;}}private static void lazy(int i, long v, int cnt) {sum[i] += v * cnt;add[i] += v;}}
5. P1471 方差
P1471 方差。
题目背景
滚粗了的 HansBug 在收拾旧数学书,然而他发现了什么奇妙的东西。
题目描述
蒟蒻 HansBug 在一本数学书里面发现了一个神奇的数列,包含 NNN 个实数。他想算算这个数列的平均数和方差。
输入格式
第一行包含两个正整数 N,MN,MN,M,分别表示数列中实数的个数和操作的个数。
第二行包含 NNN 个实数,其中第 iii 个实数表示数列的第 iii 项。
接下来 MMM 行,每行为一条操作,格式为以下三种之一:
操作 111:1 x y k ,表示将第 xxx 到第 yyy 项每项加上 kkk,kkk 为一实数。
操作 222:2 x y ,表示求出第 xxx 到第 yyy 项这一子数列的平均数。
操作 333:3 x y ,表示求出第 xxx 到第 yyy 项这一子数列的方差。
输出格式
输出包含若干行,每行为一个实数,即依次为每一次操作 222 或操作 333 所得的结果(所有结果四舍五入保留 444 位小数)。
输入输出样例 #1
输入 #1
5 5
1 5 4 2 3
2 1 4
3 1 5
1 1 1 1
1 2 2 -1
3 1 5
输出 #1
3.0000
2.0000
0.8000
说明/提示
关于方差:对于一个有 nnn 项的数列 AAA,其方差 s2s^2s2 定义如下:
s2=1n∑i=1n(Ai−A‾)2s^2=\frac{1}{n}\sum\limits_{i=1}^n\left(A_i-\overline A\right)^2s2=n1i=1∑n(Ai−A)2
其中 A‾\overline AA 表示数列 AAA 的平均数,AiA_iAi 表示数列 AAA 的第 iii 项。
数据规模:
| 数据点 | NNN | MMM | 备注 |
|---|---|---|---|
| 1∼31\sim31∼3 | N≤8N\le 8N≤8 | M≤15M\le 15M≤15 | - |
| 4∼74\sim74∼7 | N≤105N\le 10^5N≤105 | M≤105M\le 10^5M≤105 | 不包含操作 333 |
| 8∼108\sim108∼10 | N≤105N\le 10^5N≤105 | M≤105M\le 10^5M≤105 | - |
思路:
首先为了维护平均数,我们可以维护一个累加和信息,求平均数的时候就用累加和 / 区间长度就可以了,那么如何表示方差呢,下面来推导下。
- ∑i=1n(Ai−Aˉ)2=(A12+Aˉ2−2∗A1∗Aˉ)+(A22+Aˉ2−2∗A2∗Aˉ)+...+(An2+Aˉ2−2∗An∗Aˉ)=(A12+A22+...+An2)−2∗Aˉ∗(A1+A2+...+An)+n∗Aˉ2=∑i=1nAi2−n∗Aˉ2{\textstyle \sum_{i = 1}^{n}} (A_{i} - \bar{A})^2 = (A_{1}^2 + \bar{A}^2 - 2 * A_{1} * \bar{A}) + (A_{2}^2 + \bar{A}^2 - 2 * A_{2} * \bar{A}) + ... + (A_{n}^2 + \bar{A}^2 - 2 * A_{n} * \bar{A}) = (A_{1}^2 + A_{2}^2 + ... + A_{n}^2) - 2 * \bar{A} * (A_{1} + A_{2} + ... + A_{n}) + n * \bar{A}^2 = {\textstyle \sum_{i = 1}^{n}} A_{i}^2 - n * \bar{A}^2∑i=1n(Ai−Aˉ)2=(A12+Aˉ2−2∗A1∗Aˉ)+(A22+Aˉ2−2∗A2∗Aˉ)+...+(An2+Aˉ2−2∗An∗Aˉ)=(A12+A22+...+An2)−2∗Aˉ∗(A1+A2+...+An)+n∗Aˉ2=∑i=1nAi2−n∗Aˉ2
- ∑i=1n(Ai−Aˉ)2n=∑i=1nAi2n−Aˉ2\frac{{\textstyle \sum_{i = 1}^{n}}(A_{i} - \bar{A})^2}{n} = \frac{{\textstyle \sum_{i = 1}^{n}} A_{i}^2}{n} - \bar{A}^2n∑i=1n(Ai−Aˉ)2=n∑i=1nAi2−Aˉ2
所以这里我们用两个数组,一个维护累加和,求平均数就用 (sum1 / size) * (sum1 / size),然后再维护一个平方累加和,求第一部分就直接用 sum2 / size,最终结果就是 sum2size−sum12size2\frac{sum2}{size} - \frac{sum1 ^ 2}{size^2}sizesum2−size2sum12。
那么要维护平方累加和,能不能在 O(1) 时间内懒更新完成呢,也是没问题的,如果没有累加和数组那肯定不能 O(1) 懒更新完,但是有了累加和,就可以化简下了,假设现在平方累加和是 sum2[i],比如是 [l,r] 区间的累加和,可以写成:(A12+A22+...+An2)(A_{1}^2 + A_{2}^2 + ... + A_{n}^2)(A12+A22+...+An2),那么现在这个范围的每一个数字都加上 k,最终平方累加和变成了:
- ((A1+k)2+(A2+k)2+...+(An+k)2)((A_{1} + k)^2 + (A_{2} + k)^2 + ... + (A_{n} + k)^2)((A1+k)2+(A2+k)2+...+(An+k)2)
再化简下变成了:
- (A12+A22+...+An2)+2∗k∗(A1+A2+...+Ak)+n∗k2(A_{1}^2 + A_{2}^2 + ... + A_{n}^2) + 2 * k * (A_{1} + A_{2} + ... + A_{k}) +n * k ^2(A12+A22+...+An2)+2∗k∗(A1+A2+...+Ak)+n∗k2
那前面的 (A12+A22+...+An2)(A_{1}^2 + A_{2}^2 + ... + A_{n}^2)(A12+A22+...+An2) 就是原来的 sum2[i],然后 2∗k∗(A1+A2+...+Ak)2 * k * (A_{1} + A_{2} + ... + A_{k})2∗k∗(A1+A2+...+Ak) 就是 2 * k * sum[i],sum[i] 就是区间累加和,然后最后的 n∗k2n * k^2n∗k2 也可以 O(1) 时间完成,所以整体都可以在 O(1) 时间内完成,不过要注意一下,由于更新 sum2 需要依赖 sum1,所以需要先更新 sum2 再更新 sum1,然后其他的就跟之前的差不多了,下面看 code。
import java.io.*;
import java.util.StringTokenizer;public class Main {public static int MAXN = 100001;public static double[] arr = new double[MAXN];public static double[] sum1 = new double[MAXN << 2];public static double[] sum2 = new double[MAXN << 2];public static double[] add = new double[MAXN << 2];public static void main(String[] args) {Kattio kattio = new Kattio();int n = kattio.nextInt();int m = kattio.nextInt();for (int i = 1; i <= n; i++) {arr[i] = kattio.nextDouble();}build(1, n, 1);double jobv = 0.0;for (int i = 1, op, jobl, jobr; i <= m; i++) {op = kattio.nextInt();if (op == 1) {jobl = kattio.nextInt();jobr = kattio.nextInt();jobv = kattio.nextDouble();add(jobl, jobr, jobv, 1, n, 1);} else if (op == 2) {jobl = kattio.nextInt();jobr = kattio.nextInt();double res = query(sum1, jobl, jobr, 1, n, 1);kattio.println(String.format("%.4f", res / (jobr - jobl + 1)));} else if (op == 3) {jobl = kattio.nextInt();jobr = kattio.nextInt();double r1 = query(sum1, jobl, jobr, 1, n, 1);double r2 = query(sum2, jobl, jobr, 1, n, 1);int c = jobr - jobl + 1;kattio.println(String.format("%.4f", r2 / c - (r1 / c) * (r1 / c)));}}kattio.flush();kattio.close();}private static double query(double[] sum, int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];}int mid = l + ((r - l) >> 1);down(i, mid - l + 1, r - mid);double res = 0;if (jobl <= mid) {res += query(sum, jobl, jobr, l, mid, i << 1);}if (jobr > mid) {res += query(sum, jobl, jobr, mid + 1, r, i << 1 | 1);}return res;}private static void add(int jobl, int jobr, double jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {lazy(i, jobv, r - l + 1);} else {int mid = l + ((r - l) >> 1);down(i, mid - l + 1, r - mid);if (jobl <= mid) {add(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {add(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}private static void down(int i, int ln, int rn) {if (add[i] != 0) {lazy(i << 1, add[i], ln);lazy(i << 1 | 1, add[i], rn);add[i] = 0;}}private static void lazy(int i, double v, int cnt) {sum2[i] += 2 * sum1[i] * v + v * v * cnt;sum1[i] += cnt * v;add[i] += v;}private static void build(int l, int r, int i) {if (l == r) {sum1[i] = arr[l];sum2[i] = arr[l] * arr[l];} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}add[i] = 0;}private static void up(int i) {sum1[i] = sum1[i << 1] + sum1[i << 1 | 1];sum2[i] = sum2[i << 1] + sum2[i << 1 | 1];}public static class Kattio extends PrintWriter {private BufferedReader r;private StringTokenizer st;public Kattio() {this(System.in, System.out);}public Kattio(InputStream i, OutputStream o) {super(o);r = new BufferedReader(new InputStreamReader(i));}public Kattio(String intput, String output) throws IOException {super(output);r = new BufferedReader(new FileReader(intput));}public String next() {try {while (st == null || !st.hasMoreTokens())st = new StringTokenizer(r.readLine());return st.nextToken();} catch (Exception e) {}return null;}public int nextInt() {return Integer.parseInt(next());}public double nextDouble() {return Double.parseDouble(next());}public long nextLong() {return Long.parseLong(next());}}}
不过这个 code 会超过空间限制。
视频里面给了 C++ 版本,用这个版本的可以过,所以直接用视频里面的 C++ 代码就行,但是上面的 java 逻辑是对的,照着翻译成 C++ 也没问题。
如有错误,欢迎指出!!!
