传染病监测（七）：为什么接触模式能颠覆防控效果预测？

一、开场故事：为何 “随机混合” 会对疫苗策略造成误导？

假设你是某市疾控中心的新手小张，领导安排你评估：若为全市小学生免费接种流感疫苗，能将全市的发病率控制在何种程度？

你打开 Excel，将人群视作“均匀搅拌的米粥”，计算得出只要 70% 的小学生接种疫苗，就能阻断流感传播。然而到了冬天，流感依旧大规模爆发 —— 成人科室人满为患，老年 ICU 不得不加床。领导将报表扔在你桌上质问：“模型是怎么构建的？”

问题就出在 “均匀搅拌” 这一假设上。在真实世界中，孩子主要与其他孩子玩耍，家长主要与同事交流，爷爷奶奶则去跳广场舞 —— 人群并非像米粥那样均匀混合，而是如同层层叠叠的 “社交网络千层饼”。

再举个例子。

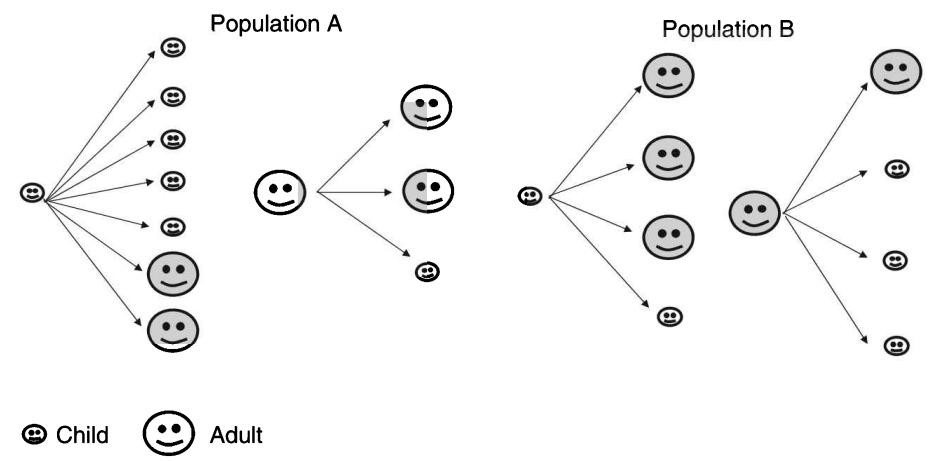
上图展示了两种人群可能的接触模式。

在总体A中，儿童的接触次数比成人多得多（7次对3次），而且儿童的大部分接触都是与其他儿童进行的；

在B种人群中，儿童与成年人的接触次数相同（4次），且主要接触成年人，而成人则主要与其他儿童接触。

如果两个群体中接种新感染（如大流行性流感）疫苗的儿童比例相同，那么后续总发病率在哪个群体中最低？

对于这个问题，一个直观的答案可能是A人群——毕竟A人群中的儿童接触其他人的机会比B人群多。但另一方面，A人群儿童的社交圈中，与其他儿童的接触比例也更高。因此，当疫苗普及导致儿童发病率下降时，A人群成年人受益的程度，远不及B人群成年人。毕竟在B人群中，儿童与成人之间存在大量直接接触。这些差异性因素使得仅凭直觉难以准确预测儿童接种疫苗对整体发病率的影响。

在本章中，我们将通过可计算的 “WAIFW 矩阵”，让模型真正理解 “谁把病传给了谁”。

二、看到数据，你应该学会？

1. 识别年龄混合的证据：从数据中认识 “同龄聚集” 现象的显著程度。

2. 构建自身的 WAIFW 矩阵：将 “儿童 - 成人” 两群体模型扩展到 3 群体、5 群体，甚至可按城乡、性别、社会经济地位等进行划分。

3. 利用血清学数据反推$\beta$：若没有经费开展万人接触调查，可通过抗体阳性率计算传播率。

4. 计算非随机混合情况下的$R_0$：摒弃 “$\beta \times N\times D$” 这一简单公式，运用下一代矩阵（Next Generation Matrix）计算真实的群体免疫阈值。

5. 预测干预效果：在接种率同为 70% 的情况下，不同接触结构所带来的结局可能存在巨大差异 —— 学会进行 “敏感性分析”。

三、从 “直觉” 到 “矩阵”：四格表入门

先不必被公式吓到，我们从最简单的场景入手：

• 仅存在两类人群：儿童（y）和成人（o）。

• 构建一个 2×2 表格，横栏表示 “被感染者的年龄”，竖栏表示 “传染源的年龄”：

WAIFW 矩阵	传染源：儿童	传染源：成人
被感染：儿童	${\beta }_{yy}$	${\beta }_{yo}$
被感染：成人	${\beta }_{oy}$	${\beta }_{oo}$

${\beta }_{yy}$表示 “一名患病儿童平均每天将疾病传染给其他儿童的人数”，其余符号含义以此类推。

此时出现一个问题：存在 4 个未知数，但仅能列出两个方程（分别对应儿童和成人的平均感染力）。如何求解呢？

有三条常用的 “约束” 路径：

1. 对称假设：${\beta }_{yo}={\beta }_{oy}$（即群体间的相互传播率相等）；

2. 比例假设：${\beta }_{yo}=k\cdot {\beta }_{oo}$（成人传染给儿童的概率是成人之间传染概率的 k 倍）；

3. 分层阶梯：对人群进行进一步细分，直至方程数量不少于未知数数量。

至于选择哪一种路径，并没有绝对的标准 —— 可先进行敏感性分析，观察不同矩阵对疫苗覆盖率预测结果的差异，再结合实际调查数据做出决策。

四、实战演练：基于 20 世纪 80 年代英国风疹数据进行计算

1）血清学回顾：儿童的感染力${\lambda }_y=13\%$/ 年，成人的感染力${\lambda }_o=4\%$/ 年。

2）估算平均感染人数：

• 儿童人口数量$N_y\approx 1100$万，成人人口数量$N_o\approx 4400$万。

• 感染期$D=11$天。

3）代入矩阵结构$R_1$（儿童 - 成人完全对称、成人之间同质）：

通过方程求解得出${\beta }_{yy}=1.8\times 10^{-8}$/ 天，${\beta }_{yo}={\beta }_{oy}={\beta }_{oo}=5.0\times 10^{-9}$/ 天。

4）下一代矩阵（NGM）：

$R_{yy}={\beta }_{yy}\cdot N_y\cdot D=2.18$

$R_{yo}={\beta }_{yo}\cdot N_y\cdot D=0.61$

$R_{oy}={\beta }_{oy}\cdot N_o\cdot D=2.43$

$R_{oo}={\beta }_{oo}\cdot N_o\cdot D=2.43$

矩阵表示为：

$
\begin{bmatrix}
2.18 & 0.61 \
2.43 & 2.43
\end{bmatrix}
$

5）计算$R_0$：求得最大特征值为 3.6。

结论：需要达到 1−1/3.6≈72% 的有效疫苗覆盖率，才能阻断风疹传播。

若采用 “成人之间接触率翻倍” 的矩阵$R_2$，$R_0$会立即升至 4.75，对应的群体免疫阈值则提高到 79%。

这正是领导所关注的：为了弥补我们对成人社交网络认知的不足，疫苗覆盖率需要再提高 7 个百分点。

五、将 “年龄” 替换为 “城乡”“性别”“职业”—— 矩阵模板保持不变

• 城乡维度：可表示为${\beta }_{uu}$、${\beta }_{ur}$、${\beta }_{ru}$、${\beta }_{rr}$，并约束${\beta }_{ur}=k\cdot {\beta }_{rr}$（由于城市人偶尔下乡，因此$k<1$）。

• 性别维度：在异性恋性传播感染（STI）模型中，天生存在 “不同性别间接触” 的特点，因此${\beta }_{fm}$、${\beta }_{mf}$远大于${\beta }_{ff}$、${\beta }_{mm}$。

• 学校班级维度：将幼儿园、小学、中学、大学、职场划分为 5×5 矩阵，就能评估 “停课两周” 究竟能使疫情曲线平缓多少。

总之，只要能够明确 “谁与谁存在接触”，就可以构建相应的 WAIFW 矩阵。

结尾彩蛋：

下次若你在会议上听到有人说 “我们假设人群均匀混合”，你可以微笑着递上这张 2×2 的小矩阵，并说：“朋友，来尝试分析一下这层‘千层饼’吧？”