路径总和Ⅲ（树）C++

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

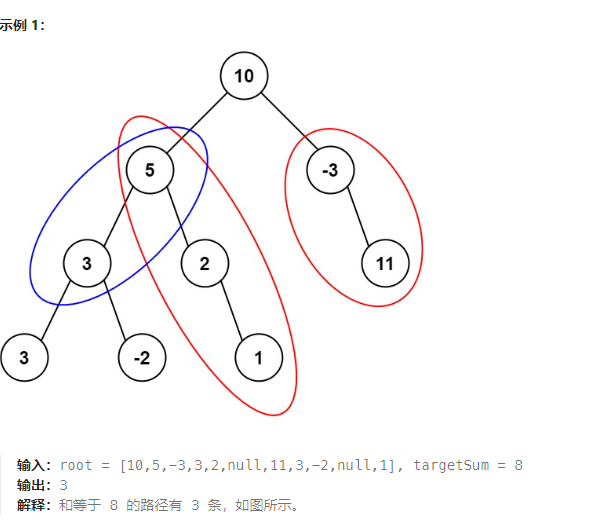
使用深度优先遍历DFS，先找到路径终点，则剩下就需要找到有多少个起点满足条件

即可转换成前缀和的问题，参考前缀和

重点：
要进行现场恢复，即在遍历结束左子树后开始遍历右子树时，哈希表中还保留着左子树的信息，这是在遍历右子树时用不到的，所以要及时恢复，否则计数会越来越大；

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:unordered_map<long long, int> map;    // key：前缀和，value：和为前缀和的个数int cnt=0;void dfs(TreeNode* node, long long sum, int targetSum){if(node == nullptr) return;sum += node->val;  // 计算前缀和long long num = sum-targetSum;if(map.find(num) != map.end()){cnt += map[num];}map[sum]++;dfs(node->left, sum, targetSum);dfs(node->right, sum, targetSum);map[sum]--;  // 恢复现场}int pathSum(TreeNode* root, int targetSum) {map[0] = 1;    // 初始化前缀和为0的个数dfs(root, 0, targetSum);return cnt;}
};