【LeetCode】算法详解#9 ---旋转图像

1.题目介绍

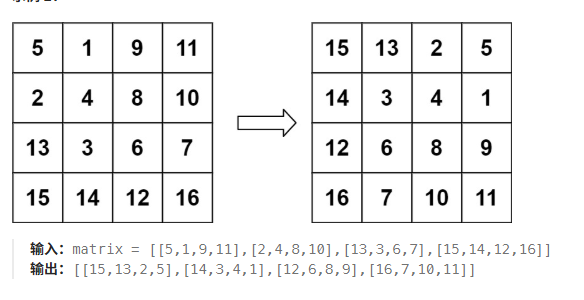
        给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

2.解决思路

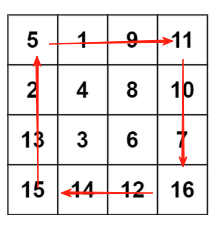
        已经知道了矩阵为n*n，现在要求顺时针旋转90°，并且不能使用额外的辅助矩阵。所以现在必须要在原矩阵的基础上进行操作。我这里有一种旋转方法，因为常规旋转 会导致元素覆盖，所以必须要找到一个旋转元素之间坐标的关系，使一轮中每个元素都能够互相赋值。经过推演（具体的推导过程48. 旋转图像 - 力扣（LeetCode））发现一个元素经旋转后相对于原元素的位置为ai,j​(new)=an−j−1, i (old)​ 。并且经过四次旋转后最终会与第一次的点重合，所以可以：利用一个临时变量记录第一次元素的位置，然后按照逆时针的顺序依次将前一个元素的值赋值给当前元素。并最终将临时变量赋值给第一次赋值的元素位置。或者另一种方案：在一轮旋转中每次都与同一个位置进行交换，这样则不需要临时变量，意思相近，这里不再展示。

3.步骤讲解

        1.创建变量n记录矩阵长度，变量temp记录第一次发生赋值的元素

        2.因为已经找出了旋转元素之间的关系，每次交换可解决四个位置的旋转。所以实际需要外层循环的次数有一个规律：行数增加1，列数减少2，第一行到n-2位置，最大行数为n/2。以这个来记录每个元素的索引。

        3.进行交换，先用临时变量记录第一次被赋值的元素值，然后按照已经推导出的等式，依次对元素旋转的目标位置进行赋值。最后一次赋值由临时变量进行赋值。可实现一轮四个元素的旋转

        4.进行循环

4.代码展示

public static void turnAround(int[][] matrix) {int n = matrix.length;//临时变量，用于记录初始元素int temp = 0;for (int i = 0; i < n/2; i++){for (int j = i; j < n-i-1; j++){//四次元素交换temp = matrix[i][j];matrix[i][j] = matrix[n-j-1][i];matrix[n-j-1][i] = matrix[n-i-1][n-j-1];matrix[n-i-1][n-j-1] = matrix[j][n-i-1];matrix[j][n-i-1] = temp;}}}

5.执行结果

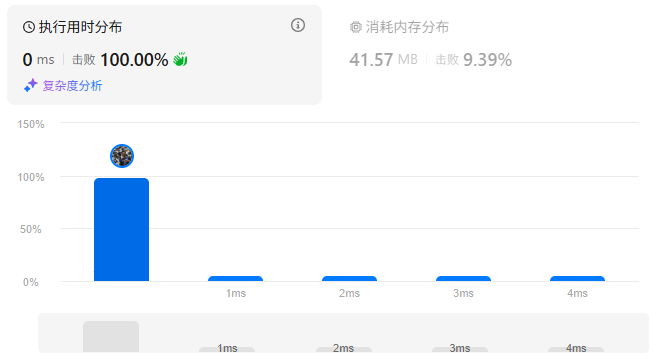
在leetcode中测试用例平均耗时0ms

内存分布41.57MB