二叉树解析

二叉树的定义

一棵二叉树是结点的一个有限集合，该集合：

• 或者为空。
• 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

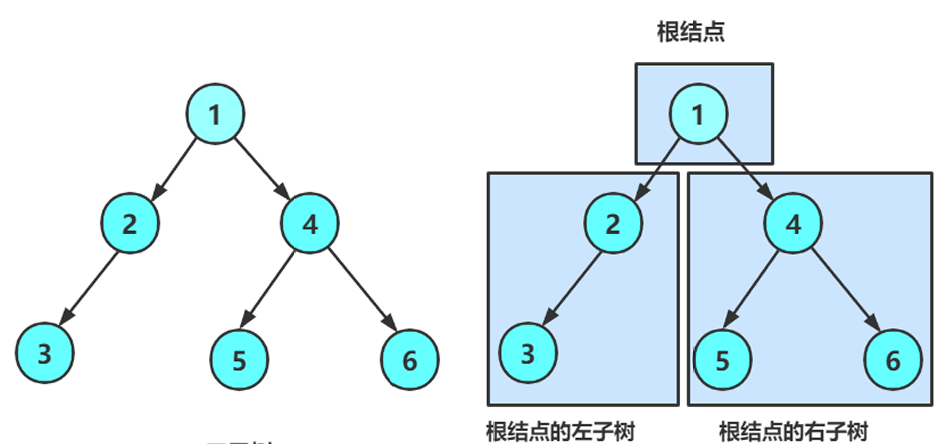
从图可知：

• 二叉树不存在度大于2的结点。
• 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树。

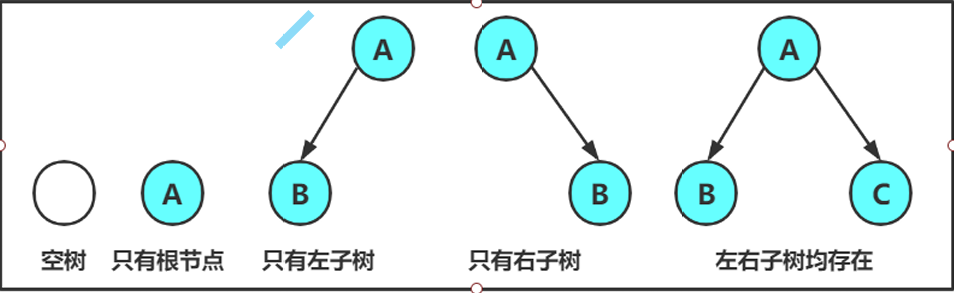
二叉树的形态

五种基本形态

三种特殊形态

1. 斜二叉树：所有结点仅含左子或右子，呈斜线状，节点数n则高度为n 。
2. 满二叉树：分支结点均有左右子树，叶子结点在同一层，深度h时节点数为(2^h - 1) 。
3. 完全二叉树：按层序编号与同深度满二叉树对应位置一致，是满二叉树少最右若干叶子的形态 。

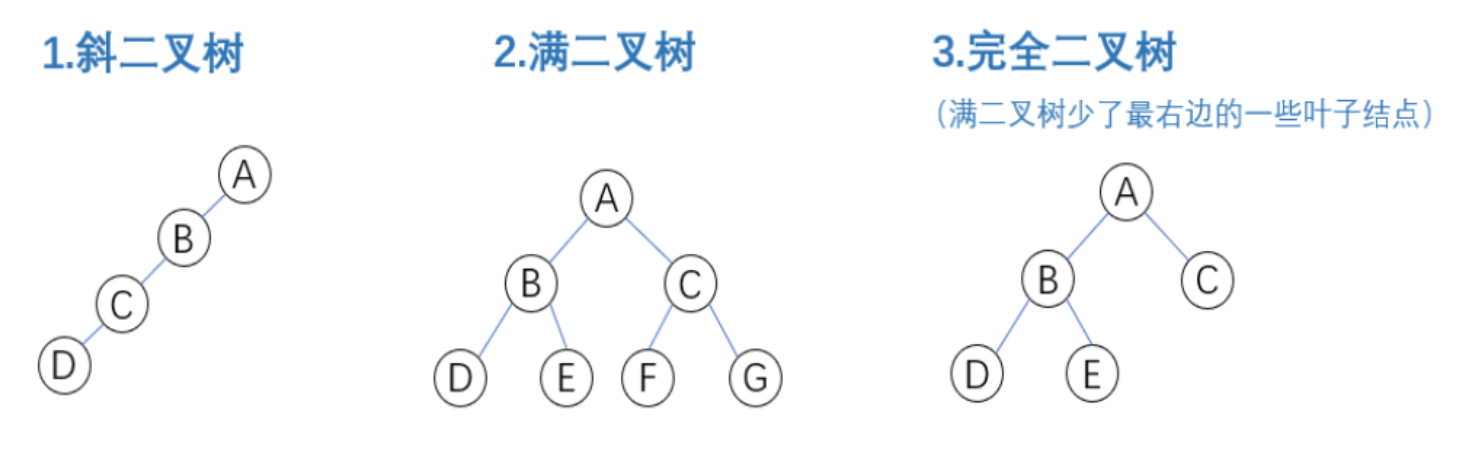
注意：满二叉树是一种特殊的完全二叉树。

二叉树的性质

1.若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有2^i-1(i>0)个结点。

2.若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是2^k-1(k>=0)。

3.对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n₀＝n₂＋1。

证明：总结点个数n = n₀ + n₁ + n₂；总结点中除根结点外，其余各结点都有一个分支进入，设m为分支总数，则有n = m + 1；又因为这些分支都是由度为1或2的结点射出的，所以有m = n₁ + 2n₂；于是有n = n₁ + 2n₂ + 1，最后将关于n的两个关系式化简得证。

4.具有n个结点的完全二叉树的深度k为log₂（n+1）为上取整。

5.对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：

• 若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点。
• 若2i+1<n，左孩子序号：2i+1，否则无左孩子。
• 若2i+2<n，右孩子序号：2i+2，否则无右孩子。

二叉树的存储

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。

1.顺序存储：

使用一组地址连续的存储单元存储，例如数组。为了在存储结构中能得到父子结点之间的映射关系，二叉树中的结点必须按层次遍历的顺序存放。具体是：

• 对于完全二叉树，只需要自根结点起从上往下、从左往右依次存储。
• 对于非完全二叉树，首先将它变换为完全二叉树，空缺位置用某个特殊字符代替（比如#），然后仍按完全二叉树的存储方式存储。

顺序存储非常适合存储接近完全二叉树类型的二叉树，对于一般二叉树有很大的空间浪费，所以对于一般二叉树，一般用下面这种链式存储。

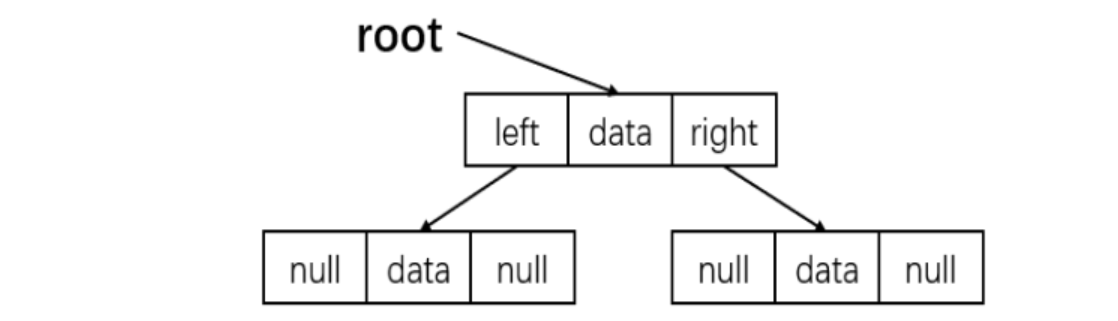
2.链式存储：

对每个结点，除数据域外再多增加左右两个指针域，分别指向该结点的左孩子和右孩子结点，再用一个头指针指向根结点。对应的存储结构：

二叉树的基本操作

二叉树的遍历

遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。

1.前中后序遍历：

二叉树由三个基本单元组成：根结点，左子树，右子树，因此存在6种遍历顺序，若规定先左后右，则只有一下三种：

• NLR：前序遍历(Preorder Traversal)—访问根结点–>根的左子树–>根的右子树。
• LNR：中序遍历(Inorder Traversal)—根的左子树–>根节点–>根的右子树。
• LRN：后序遍历(Postorder Traversal)—根的左子树–>根的右子树–>根节点。

class Node {int val;Node left;Node right;Node(int val) {this.val = val;this.left = null;this.right = null;}
}public class BinaryTreeTraversal {// 前序遍历：根 -> 左 -> 右void preOrder(Node root) {if (root == null) {return;}// 访问根节点，这里简单打印节点值示例System.out.print(root.val + " "); preOrder(root.left);preOrder(root.right);}// 中序遍历：左 -> 根 -> 右void inOrder(Node root) {if (root == null) {return;}inOrder(root.left);// 访问根节点，这里简单打印节点值示例System.out.print(root.val + " "); inOrder(root.right);}// 后序遍历：左 -> 右 -> 根void postOrder(Node root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);// 访问根节点，这里简单打印节点值示例System.out.print(root.val + " "); }
}

仔细观察先序、中序、后序的结点访问顺序可以发现：

2.层序遍历：

除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

二叉树的基本操作

class Node {int val;Node left;Node right;Node(int val) {this.val = val;this.left = null;this.right = null;}
}public class BinaryTreeOperations {// 获取树中节点的个数int size(Node root) {if (root == null) {return 0;}// 根节点 + 左子树节点数 + 右子树节点数return 1 + size(root.left) + size(root.right); }// 获取叶子节点的个数int getLeafNodeCount(Node root) {if (root == null) {return 0;}// 左右子节点都为空，是叶子节点if (root.left == null && root.right == null) { return 1;}// 左子树叶子数 + 右子树叶子数return getLeafNodeCount(root.left) + getLeafNodeCount(root.right); }// 获取第 k 层节点的个数（k 从 1 开始）int getKLevelNodeCount(Node root, int k) {if (root == null || k < 1) {return 0;}if (k == 1) {// 第 1 层只有根节点return 1; }// 递归求左、右子树第 k - 1 层节点数之和return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1); }// 获取二叉树的高度int getHeight(Node root) {if (root == null) {return 0;}// 树的高度 = 1 + 左右子树较高的高度int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return 1 + Math.max(leftHeight, rightHeight); }// 检测值为 value 的元素是否存在，存在返回对应节点，不存在返回 nullNode find(Node root, int val) {if (root == null) {return null;}if (root.val == val) {return root;}// 先在左子树找Node leftFind = find(root.left, val); if (leftFind != null) {return leftFind;}// 左子树没找到，在右子树找return find(root.right, val); }// 层序遍历（借助队列实现）void levelOrder(Node root) {if (root == null) {return;}java.util.LinkedList<Node> queue = new java.util.LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {Node node = queue.poll();// 访问节点，这里简单打印节点值示例System.out.print(node.val + " "); if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}}// 判断一棵树是不是完全二叉树（借助队列，按层遍历特性判断）boolean isCompleteTree(Node root) {if (root == null) {return true;}java.util.LinkedList<Node> queue = new java.util.LinkedList<>();queue.offer(root);boolean isLeafStage = false;while (!queue.isEmpty()) {Node node = queue.poll();if (isLeafStage) {// 进入叶子阶段后，后续节点必须是叶子（无左右子节点）if (node.left != null || node.right != null) { return false;}} else {if (node.left != null && node.right != null) {queue.offer(node.left);queue.offer(node.right);} else if (node.left != null && node.right == null) {queue.offer(node.left);isLeafStage = true;} else if (node.left == null && node.right != null) {// 左空右不空，不是完全二叉树return false; } else {isLeafStage = true;}}}return true;}
}