csp基础知识——递推

1.pell数列：起初是pell数列，产生了dp的解题思路。

假设ai是pell数列，那么有以下规律：

a1=1;a2=2;a3=2*a2+a1;...ai=2*a(i-1)+a(i-2)...

那么求ak=？

有两种解题思路：一种是递推，还有一种是迭代。递推的话，上面的公式已经很明显了，直接一个for循环搞定；迭代也是用for循环，不过循环内部的三个变量要相互变换。。。

int a = 1, b = 2, t;

for(int i = 3; i <= k; ++i)
{
t =  2*b+a;

          a = b;//更新a
b = t;//更新b

       }//最后输出b

2.后来是铺方块问题：在规定长度2*n的格子里，铺方块2*1 

题目描述：小X对着一个长为N宽为2的矩形棋盘发呆，突然想到棋盘上不仅可以放棋子，还可以放多米诺骨牌。每个骨牌都是一个长为2宽为1的矩形，当然可以任意旋转，一共有三个颜色的骨牌。小X想知道在骨牌两两不重叠的前提下，铺满有多少种排列方式。

基本思路就是先考虑排法，再考虑颜色。

dp[0] = 1
dp[1] = 1
dp[i] = dp[i-1] + dp[i-2] （放一个竖牌 或 放两个横牌）

对于每种铺法，计算骨牌个数，再计算上色

假设每块骨牌有 3 种颜色。

如果铺法用了 k 个骨牌，总上色方案数为：dp[n] × 3^k，用快速幂方法

快速幂？  

那么如何计算骨牌数k? 一种思路是 总格子数/单个骨牌所占格子数，即k=2*n/1*2=n 

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;const int MOD = 1e9 + 7;int main() {int n;cin >> n;// 预处理dpvector<long long> dp(n + 1, 0);dp[0] = 1;  // 空棋盘dp[1] = 1;  // 只能竖着放for (int i = 2; i <= n; ++i) {dp[i] = (dp[i - 1] + dp[i - 2]) % MOD;}// 快速幂计算 3^n % MODlong long power3 = 1, base = 3;int k = n;  // 一共会放 n 块骨牌while (k > 0) {// 2^4=4^2=16^1if (k % 2 == 1) power3 = (power3 * base) % MOD;//指数是奇数，就拿出一个底数，乘到结果项里base = (base * base) % MOD;//现在指数k必然是偶数，底数base增倍，指数减下来k /= 2;}long long ans = (dp[n] * power3) % MOD;cout << ans << endl;return 0;
}

---

3.有一道题目，可以深入了解dp的含义：

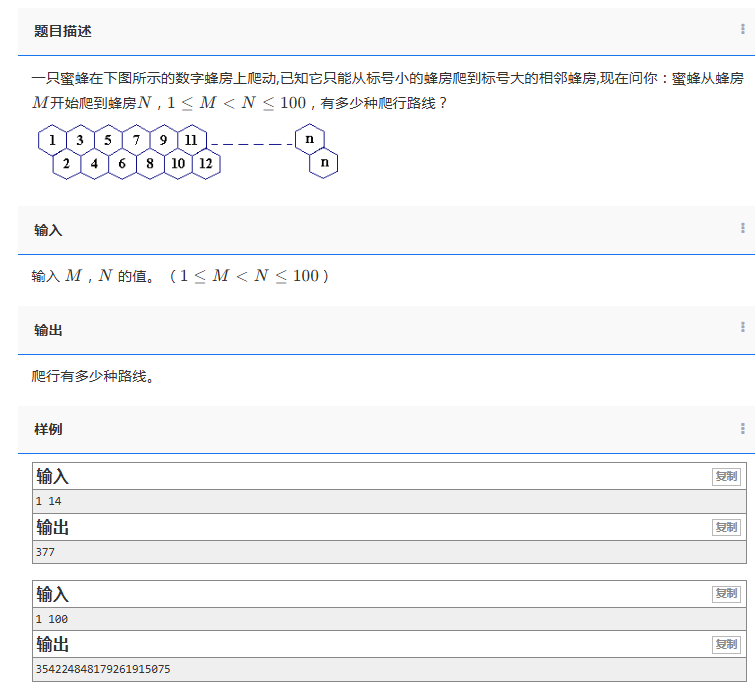
#include <bits/stdc++.h>
using namespace std;// 高精度加法
string add(string a,string b){string c;reverse(a.begin(), a.end());reverse(b.begin(), b.end());int la = a.size(), lb = b.size();int n = max(la, lb);int y = 0; // 进位for (int i = 0; i < n; i++) {int x = y; // 当前位的总和初始为进位if (i < la) x += a[i] - '0';if (i < lb) x += b[i] - '0';c += (x % 10) + '0';y = x / 10;}if (y!=0) c += y + '0';reverse(c.begin(), c.end());return c;
}int main(){vector<string> dp(110);//从1到n的路径个数dp[0]="0";dp[1]="1";dp[2]="1";// 构造 dp[1] 到 dp[100]for(int i=3;i<=100;i++){dp[i] = add(dp[i-1], dp[i-2]);}int n, m;cin >> m >> n;// 从m~n路径数等价于从1~m-n+1的路径数，本质上都是一样的，从某一起始点开始//[m]-m+1=1//[n]-m+1=n-+1cout << dp[n - m + 1] << endl;
}