当前位置：首页 > news >正文

【菜狗学聚类】时间序列聚类主要方法—20250722

news 2025/7/23 5:15:13

目前聚类的主要方法分类

时间序列聚类的挑战

1、时间序列的表示（Representation）

1.1 原始时间序列

1.2 PAA分段聚合近似

1.3 APCA（自适应分段常数近似）——“数据变化情况”

编辑

1.4 SAX（符号聚合近似）

1.5 DFT（离散傅里叶变换）

2、距离度量

2.1 欧几里得距离（Euclidean）

2.2 动态时间规整（Dynamic Time Warping, DTW）

2.3 最小距离（Minimum Distance, MINDIST）

3、原型（Prototype）

3.1 中位序列（Medoid）

3.2 平均序列（Average）

4、聚类算法（Clustering Algorithm）

4.1 KMedoids（K中心序列）

4.2 KMeans（K均值）

4.3 层次凝聚聚类（Hierarchical Agglomerative Clustering, HAC）

PyPOTS

1. 支持聚类任务的模型

2. 处理部分观察数据（缺失数据）

3. 使用多种距离度量进行聚类

4. 自动化和可扩展性

5. 使用统一的接口和文档

6. 集成的质量保证

目前聚类的主要方法分类

1、基于模型的方法

在这种方法中，每个时间序列都由模型参数表示，它可以根据时间序列的潜在特征揭示相似性。然而，它受到模型假设和准确估计参数的困难的限制。此外，当集群彼此靠近时，它往往会遇到可扩展性问题和性能下降的问题。

2、基于特征的方法

该方法将每个时间序列转换为特征向量，从而允许使用成熟的聚类技术。然而，一个主要限制是时间序列固有的时间信息丢失，这可能会影响聚类的准确性。

3、基于形状的方法

这种方法通过对齐原始时间序列并使用动态时间扭曲（DTW）或欧几里得距离等距离度量来提取模式，直接比较原始时间序列。虽然它可以捕获时间相似性，但它的计算成本很高，特别是对于大型数据集。

时间序列聚类的挑战

表示/降维（Representation/Reduction）

时间序列数据通常是高维的，尤其当时间序列很长时，直接进行聚类计算开销大且效果可能不佳。为了高效处理，通常会使用一些降维技术，将时间序列表示为更简单的形式，减少维度的同时保留数据的核心特征。

距离度量（Distance metrics）

计算时间序列之间的相似性或差异性是一个挑战。传统的距离度量方法（如欧几里得距离）无法很好地捕捉时间序列中的时序关系。更先进的方法，如动态时间规整（DTW），能更好地处理时间序列中的位移和扭曲，适用于时间序列数据。

原型选择（Prototype selection）

聚类算法中，定义聚类的“原型”是至关重要的，原型是每个聚类类别的代表。原型的选择会直接影响聚类的质量、计算复杂度及所选择的算法。

聚类算法（Clustering algorithm）

不同的聚类算法有不同的分组方式，各自有优缺点。算法的选择会影响数据的潜在结构是否被有效捕捉，以及最终如何形成聚类。

1、时间序列的表示（Representation）

高维时间序列数据会带来许多问题，尤其是在大数据集中的聚类任务。每个时间序列可能包含大量时间点，这会增加内存使用，并使得计算任务变得更为复杂和容易受到噪声的影响。因此，在进行聚类之前，通常会进行降维处理。

降维的主要动机：

减少内存使用：通过减少需要存储的数据点，降维可以减小数据集的内存占用，尤其是对于包含成千上万时间点的大数据集。
减少距离计算的计算成本：计算时间序列间的距离通常是最耗费计算资源的步骤。降维后，计算距离会更高效，减少计算时间。
避免噪声干扰：时间序列数据通常包含噪声，降维技术能帮助平滑数据，减少噪声对距离计算的干扰。

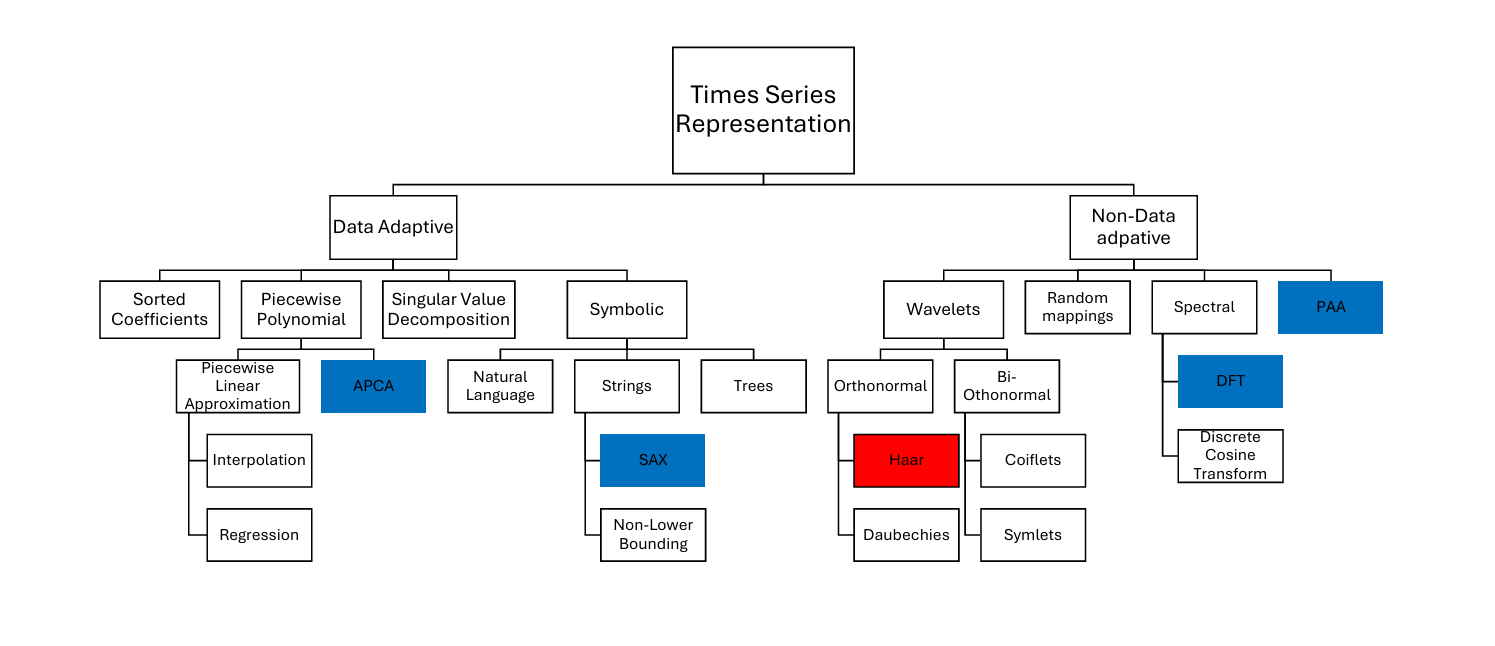
Data Adaptive方法能够根据数据本身的特性动态调整时间序列的表示，这意味着它们能够更好地捕捉数据中的潜在模式和变化。
Non-Data Adaptive方法则依据固定的规则或算法处理时间序列，更倾向于快速的计算和分析，适合处理大规模数据。

1.1 原始时间序列

原始时间序列数据是最完整的表示方式，能充分展示观察到的现象的变化和时间依赖关系。这种表示方式对于捕捉复杂的模式和动态特性非常有用。然而，原始数据的高维度、计算成本以及噪声和不规则性可能带来问题。此外，原始数据可能会因为没有抽象化而导致过拟合。因此，尽管原始时间序列数据包含大量信息，但其在使用时需要采取适当的预处理措施，以避免这些问题。

1.2 PAA分段聚合近似

PAA方法通过将时间序列划分为等长的段，并用每段的平均值来表示该段，从而简化时间序列。PAA的主要目标是减少时间序列的维度，同时保留其关键特征，使得时间序列数据更加简洁易于分析。

PAA转换的数学公式：

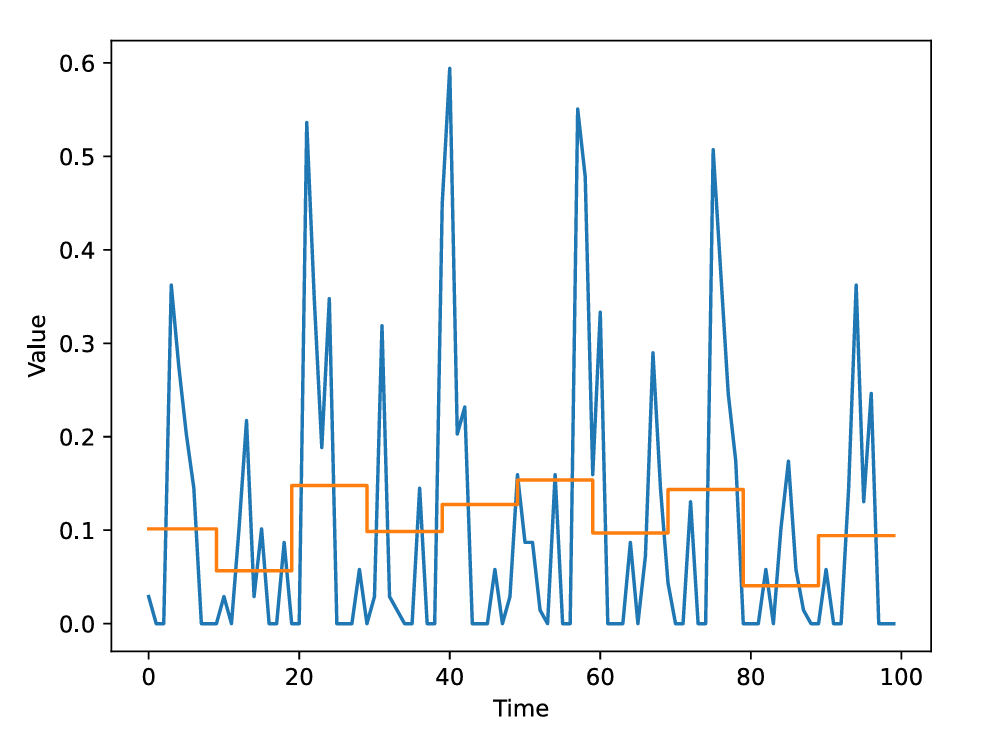
1.3 APCA（自适应分段常数近似）——“数据变化情况”

APCA 是在 PAA 的基础上进行改进的一种方法，它采用自适应的方法来划分时间序列的段，而不是使用固定大小的段。APCA 通过动态调整段的长度，以最小化表示与原始时间序列之间的误差。

APCA的表示方式：

APCA的优点：

适应数据特征：APCA 通过自适应地调整段的长度，能够更好地捕捉局部模式，表现出较高的适应性。
高效的降维：与 PAA 类似，APCA 通过用常数值代表每个段来减少时间序列的维度。
更好的局部模式表示：由于段的长度可以根据数据的特征调整，APCA 能更精确地表示那些局部的重要模式。
灵活性：通过调整段的数量，APCA 也可以在不同的分辨率下进行分析。
噪声抑制：和 PAA 一样，APCA 通过对段进行平均，能够平滑掉小的噪声变化，减少噪声对分析结果的影响。

APCA的缺点：

过度平滑：尽管 APCA 能减少噪声，但它也可能平滑掉那些较少出现但仍然重要的模式。这样会导致模型忽视一些关键的变化模式。
依赖数据特征：APCA 的效果高度依赖于数据的特征，如果数据中没有明显的模式或变化，APCA 的效果可能不如 PAA。
参数敏感性：APCA 依赖于参数设置，特别是段的长度调整，这使得它可能需要更多的调优来找到最优的表示方式。这使得它在某些情况下变得更为复杂。

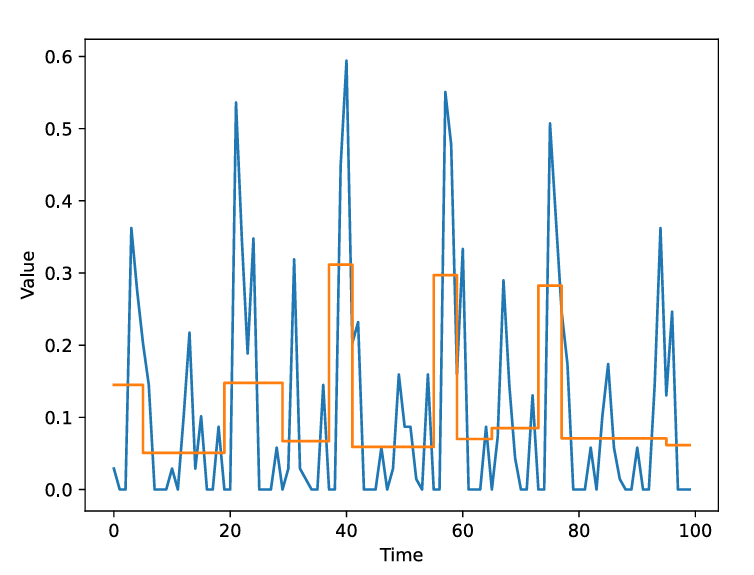
1.4 SAX（符号聚合近似）

SAX 是一种时间序列数据的降维和符号表示方法。它的目标是将连续的时间序列转换为离散的符号表示，通常称为 字母表（alphabet）。

SAX 转换的步骤：

PAA降维：首先，通过 PAA（分段聚合近似）方法对数据进行降维，将原始时间序列转换成较低维度的表示。
离散化：然后，对降维后的数据进行离散化处理。SAX 的离散化方法是利用正态分布（假设归一化后的时间序列遵循高斯分布），使用断点来将数据划分成几个范围，每个范围对应字母表中的一个符号。
生成字：最后，将降维后的每个数据点映射到一个符号，从而生成时间序列的符号表示（即字）。

SAX的优点：

高效降维：SAX 能显著减少时间序列的维度，使得后续的计算更加简便。
抗噪声：SAX 的分段聚合和符号离散化使得它对小的变化和噪声具有鲁棒性。
灵活性：可以调整分析的分辨率，包括分段的数量（PAA的大小）和字母表的大小（符号的数量）。
支持离散算法：通过将时间序列转换为符号字符串，SAX 支持一些仅适用于离散数据的经典算法，比如哈希算法、马尔科夫模型和字符串匹配算法（如汉明距离等）。

SAX的缺点：

信息丢失：SAX 在转换过程中固有地会丢失一些细节信息，尤其是局部模式或高频变化。
假设高斯分布：SAX 假设时间序列的正态化后符合高斯分布，这一假设并不适用于所有时间序列。
固定段大小：SAX 依赖于等大小的时间段，这可能无法捕捉到不同尺度或不同分辨率下的局部模式。
不适用于非平稳时间序列：SAX 最适用于平稳时间序列（即统计性质不随时间变化的数据），对于具有趋势或季节性变化的非平稳时间序列，可能效果较差。
符号表示依赖于参数：SAX 的表示质量和聚类效果高度依赖于参数的选择（如PAA段的数量和字母表的大小）。

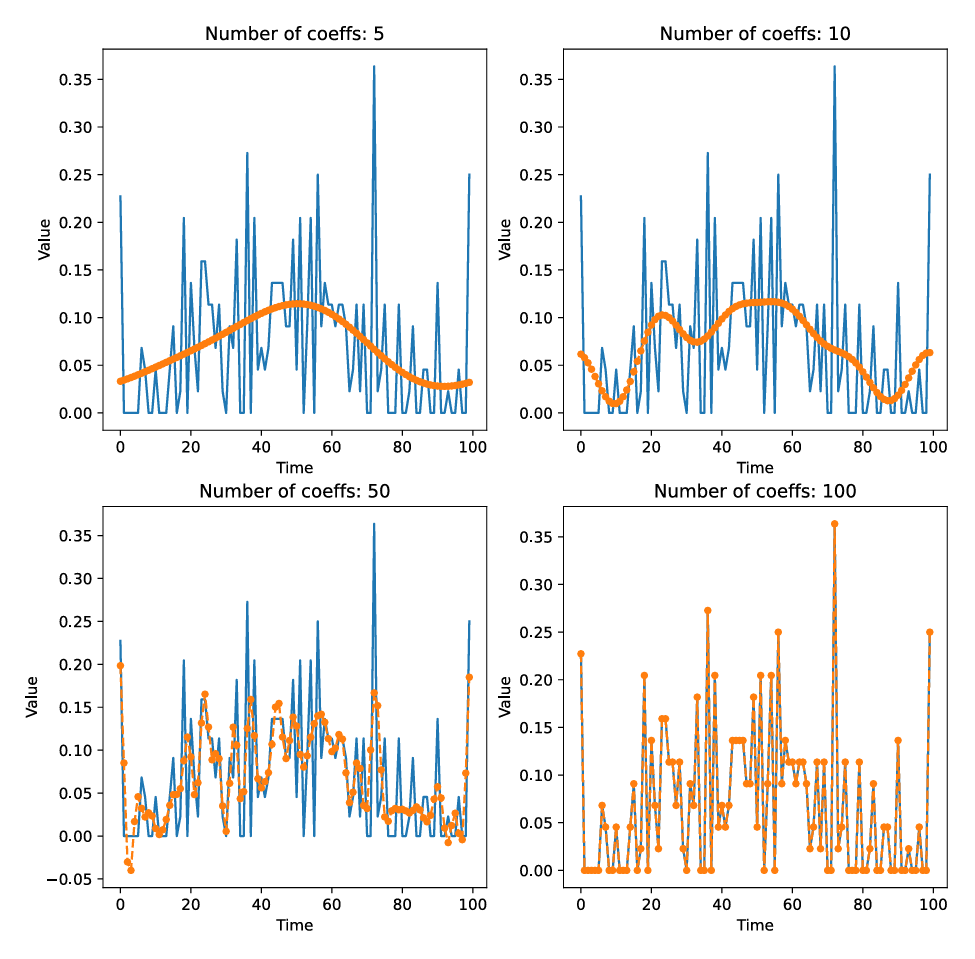
1.5 DFT（离散傅里叶变换）

傅里叶变换通过将时间序列数据从时间域转换到频率域来分解数据，表示为一组正弦波函数的和。

傅里叶变换的核心思想是：任何复杂的波形（比如时间序列数据）都可以通过多个简单的波形（正弦波和余弦波）叠加而成。想象一下，如果你听到一首音乐，它的声音其实是很多频率（高音、低音）组成的。傅里叶变换就是把这些音符“分解”成不同频率的成分。

通过 DFT，我们可以将时间序列转换为 频率域 的数据，告诉我们这个信号中有多少是由不同频率的波动组成的。

DFT的优点：

高效降维：通过只保留主频率成分，傅里叶变换可以显著降低时间序列的维度。
处理周期性模式：傅里叶变换特别擅长捕捉时间序列中的周期性或循环行为。
平移不变性：DFT 能够有效处理时间序列的平移版本（即时间序列的偏移）。
噪声过滤：通过丢弃高频成分（通常与噪声相关），傅里叶变换能够提高聚类性能。

DFT的缺点：

丧失时间信息：傅里叶变换将时间序列转换到频率域，丧失了原始数据的时间顺序。
非平稳性：傅里叶变换假设时间序列是平稳的，意味着其统计特性在时间上不变。而许多现实世界的时间序列并不符合这一假设。
对非周期数据敏感：傅里叶变换主要适用于周期性强的时间序列。对于没有周期性或波动较小的时间序列，傅里叶变换可能无法提供有效的频率成分。

2、距离度量

度量距离可能是聚类算法最关键的方面。它们定义度量空间的属性和特征，要聚类的元素将在其中进行比较和关联。因此，在聚类时，规定距离是必不可少的，因为它们定义了元素之间的关系和差异，以将它们划分为不同的组或类。

在时间序列聚类中，不同的指标可能意味着比较时间序列的不同方式，例如使用欧几里得距离查找每个时间步长中的相似性，或使用动态时间扭曲（DTW）查找形状相似的时间序列。可以考虑其他距离，但它们属于基于特征或基于模型的聚类类别，例如使用隐马尔可夫模型 [31] 或 ARMA 过程 [40] 来查找具有相似自相关的时间序列。

2.1 欧几里得距离（Euclidean）

欧几里得距离是一种用于量化欧几里得空间中两点之间相似度的度量方法。对于时间序列数据，计算两个时间序列之间的欧几里得距离，就是求对应点之间差值的平方和的平方根。

给定两个长度相同的时间序列 X = (x₁, x₂, ..., xₙ) 和 Y = (y₁, y₂, ..., yₙ)，欧几里得距离定义为：

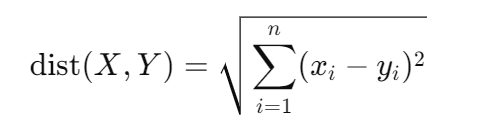
每个时间步之间存在一一对应的关系。

欧几里得距离是一种计算效率高且直观的方法，能够衡量时间序列之间的全局相似性。其优势在于简洁性，适合大数据集和实时应用，尤其是当时间序列数据是均匀采样且对齐时。
但是，欧几里得距离对数据的尺度非常敏感，对时间轴的位移也不具备鲁棒性，并且假设时间步长是相等的，这些限制可能会影响聚类结果，尤其是对于那些具有不同时间特征或不规则采样的时间序列。

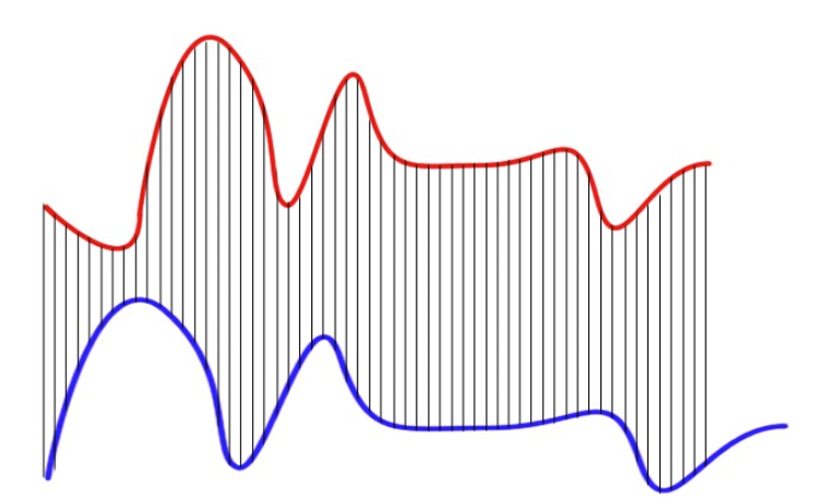
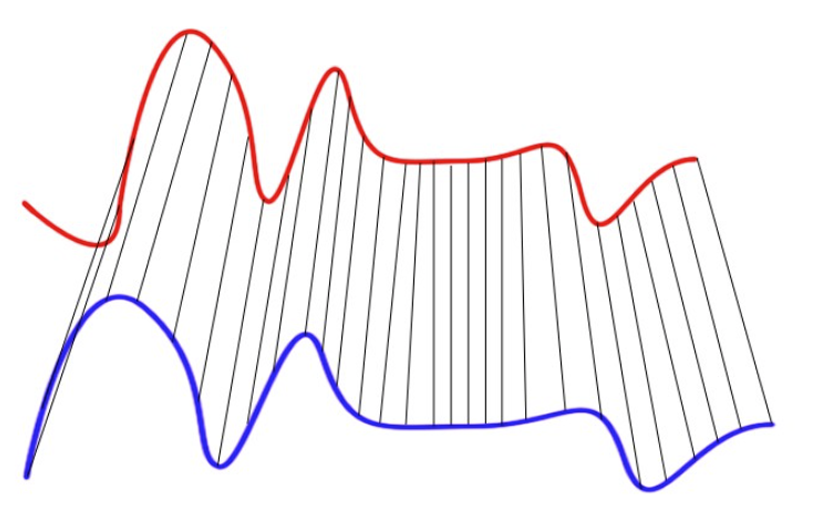
2.2 动态时间规整（Dynamic Time Warping, DTW）

动态时间规整（DTW）是一种度量两个时间序列相似度的距离度量方法，它通过考虑时间序列之间所有可能的对齐方式来进行比较。与传统的距离度量方法不同，DTW允许灵活的对齐，能够适应时间轴上的位移和扭曲。

DTW通过构建一个成本矩阵，其中每个元素表示两个时间序列对应时间点之间的距离。然后，DTW使用动态规划算法找到具有最小累积距离的路径，从而提供时间序列之间的相似度度量。
DTW的计算复杂度为O(NM)，其中N和M分别是X和Y的维度。虽然DTW能很好地处理时间扭曲并提供详细的对齐信息，这使得它在时间序列聚类中非常有用，但它的计算复杂度较高，且对噪声较为敏感，内存消耗也较大，尤其是对于大数据集来说，可能会面临挑战。

2.3 最小距离（Minimum Distance, MINDIST）

最小距离度量（MINDIST）是一种用于比较时间序列的度量方法，它通过计算时间序列对应段之间的最小距离来衡量相似度，特别适用于使用SAX、PAA或APCA等降维技术时。

3、原型（Prototype）

在时间序列聚类中，寻找原型（prototype）是一个非常重要的步骤。原型用于概括一个聚类内部时间序列的主要特征，便于进行聚类内的比较与总结。原型的选取对聚类的质量有着直接影响：原型越能代表该类的整体特征，聚类效果就越好。

3.1 中位序列（Medoid）

定义：中位序列是最常用的一种聚类原型，因为实现简单、计算代价低。
做法：直接从数据集中选取某条实际存在的时间序列作为该类的代表（原型）。选中的就是让这个序列与同类其他序列的总距离最小，也就是前面提到的Steiner序列。

总结：中位序列就是“从已有的里面选一个最能代表大家的”。

3.2 平均序列（Average）

定义：平均序列是通过对聚类中的所有时间序列逐点平均来得到的一个“新”的时间序列，也被称为质心（centroid）。
情况1（使用欧几里得距离）：如果用欧几里得距离这种刚性距离，计算平均很简单：每个时间点的所有序列的数值取平均。
情况2（使用DTW距离）：但如果用的是动态时间规整（DTW）这种允许对齐变形的距离，平均就变得很复杂，特别是当序列数量多的时候。

4、聚类算法（Clustering Algorithm）

时间序列聚类具有挑战性，因为时间序列数据本身具有时间依赖性。不过，经典的聚类算法，比如KMeans、KMedoids和层次凝聚聚类（Hierarchical Agglomerative Clustering, HAC），都可以通过**使用合适的距离度量（2.2节）和原型选择方法（2.3节）**来适配时间序列数据。本节讨论这些算法的原理和特点。

4.1 KMedoids（K中心序列）

定义：KMedoids是一种划分型聚类算法，它将数据划分为k个簇。每个样本被分配给距离该簇代表（medoid）最近的簇。
算法过程：
- 先给定簇的数量k。
- 初始选k个medoid（簇代表）。
- 每个数据点分配到最近的medoid。
- 然后更新每个簇的medoid（重新选择使得与其他簇成员距离总和最小的那个）。
- 反复迭代直到收敛。
优缺点：
- 优点：
  - 对离群点更鲁棒（比KMeans好）。
  - 可适配不同的距离度量（比如DTW等）。
- 缺点：
  - 计算复杂度高，尤其是数据量大时。

解析：
KMedoids适合时间序列聚类，因为它能直接基于DTW或其他相似性度量来找代表序列（medoid），不用平均，这样避免了DTW平均难算的问题。但代价是计算慢，适合数据量不太大的场景。

4.2 KMeans（K均值）

定义：KMeans也是一种划分型聚类算法，它的目标是最小化每个簇内的方差。
算法过程：
- 先给定簇的数量k。
- 随机选k个初始质心（centroid，平均序列）。
- 把每个数据点分到最近的质心。
- 更新每个质心（簇内所有样本的平均）。
- 重复迭代直到质心稳定。
优缺点：
- 优点：
  - 实现简单。
  - 可扩展到大数据集。
  - 可以替换距离度量（比如用DTW代替欧几里得）。
- 缺点：
  - 对初始质心敏感，可能陷入局部最优。
  - 容易受噪声影响。

解析：
KMeans如果用欧几里得距离，非常快，但对时间序列不够好。如果改用DTW就可以改善，但此时“平均序列”很难计算（因为DTW平均计算复杂），所以KMeans在时间序列聚类里应用受限。

4.3 层次凝聚聚类（Hierarchical Agglomerative Clustering, HAC）

定义：HAC是一种层次型聚类方法，通过不断合并最近的两个簇来建立一个嵌套的簇层级。
算法过程：
- 每个时间序列开始时都是独立的簇。
- 不断找到最近的两个簇，合并。
- 直到所有时间序列都合并为一个大簇，生成一棵层次树（dendrogram，树状图）。
优缺点：
- 优点：
  - 不需要提前指定k。
  - 可以根据后续的评价指标（如轮廓系数）来选最优的簇数。
  - 可适配各种距离度量。
  - 结果稳定、可复现。
- 缺点：
  - 计算复杂度高，不适合超大规模数据集。

解析：
HAC很适合时间序列聚类，特别是想要得到**层次结构（比如：大致相似的分组下再细分）**的场景。而且不需要事先知道k值，适合探索性分析。但因为它也是基于两两距离，计算起来很慢。

PyPOTS

PyPOTS提供了一些强大的工具，尤其是针对**部分观察时间序列（POTS）**的数据。下面是PyPOTS能够帮助你进行时间序列聚类的几个方面：

1. 支持聚类任务的模型

PyPOTS包含了多个用于时间序列聚类的模型。例如：

CRLI（Clustering Representation Learning on Incomplete time-series data）：这是一个基于神经网络的聚类方法，专门设计用来处理缺失数据的时间序列聚类。
VaDER（Variational Deep Embedding with Recurrence）：这是一个变分深度嵌入方法，利用循环神经网络（RNN）进行时间序列聚类，适用于处理具有缺失值的时间序列。

这些模型能够自动从时间序列数据中学习特征，并将相似的时间序列分到同一簇。

2. 处理部分观察数据（缺失数据）

时间序列数据中常常包含缺失值，而PyPOTS特别针对这一点进行了优化。传统的聚类方法可能无法有效地处理不完整的数据，但PyPOTS通过其专门的插补算法（如BRITS、SAITS等）来填补缺失值，使得即便数据不完整，聚类过程依然能够顺利进行。

3. 使用多种距离度量进行聚类

在时间序列聚类中，选择合适的距离度量是非常关键的。PyPOTS支持多种距离度量方法，尤其是：

基于概率的距离：例如Bayesian Temporal Tensor Factorization（BTTF）模型，用于时间序列预测和聚类。
基于神经网络的距离：如使用自注意力（SAITS）或变分深度嵌入（VaDER）等方法，这些方法通常能更好地处理复杂的时间序列数据，尤其是在处理具有长期依赖关系或不规则时间步的数据时。