【计算机组成原理】符号位OF、ZF、CF、SF详解

四个符号位具体含义与逻辑表达式

标志位	英文全称	含义说明	适用数据类型	判断逻辑表达式
OF	Overflow Flag	有符号数运算中溢出标志。结果超出了补码能表示的范围。	有符号数	OF = Cn异或Cn-1
CF	Carry Flag	无符号数运算中进位标志。加法产生了进位，减法产生了借位。	无符号数	CF = C0异或Cn
ZF	Zero Flag	结果是否为0。	通用	ZF = 1表示结果为0
SF	Sign Flag	结果的符号位（即最高位），表示结果是否为负（仅对有符号数有意义）。	有符号数	SF = 结果的最高位

OF解析

        OF表示有符号数的加减运算是否溢出，其值为符号位进位（Cn）与数值位最高位进位（Cn-1）的异或。

        推断出这个逻辑表达式的基础在于，如果有符号数的加减运算出现溢出，只有下面两种情况：

        1、同符号数相加结果异号；

        2、负－正得正，正-负得负。

        那么只需要简单列举一下能出现溢出的所有情况，即可推出表达式：

具体情形	符号位进位（Cn）	溢出情况下，数值位最高位进位（Cn-1）
正数+正数	0+0，Cn=0	正数加正数得负数则溢出，故Cn=1
负数+负数	1+1，Cn=1	负数+负数得正数则溢出，故Cn=0
负数-正数	1+1，Cn=1	负数-正数得正数则溢出，故Cn=0
正数-负数	0+0，Cn=0	正数-负数得负数则溢出，故Cn=1

        所以从上表显然当Cn异或Cn-1时，发生溢出，即OF=1。

CF解析

        CF表示无符号数的加减运算是否溢出，其值为符号位进位（Cn）与最低进位输入（C0）的异或。

        这应该怎么理解呢？首先需要知道一个前提，无符号数虽然没有补码的概念，但是无符号数的加减运算同样属于模运算的范畴，所以减去一个无符号数B等于+（-B），这里的-B应当等于M-B，即B的所有位数按位取反后再加1（类似于补码的计算方法）。

        有了上面这个基础之后，当两个无符号数相加，C0=0（控制端），若Cn=1，则发生了溢出。

        若两个无符号数相减，如果发生溢出（被减数小于减数）的情况如下图所示：

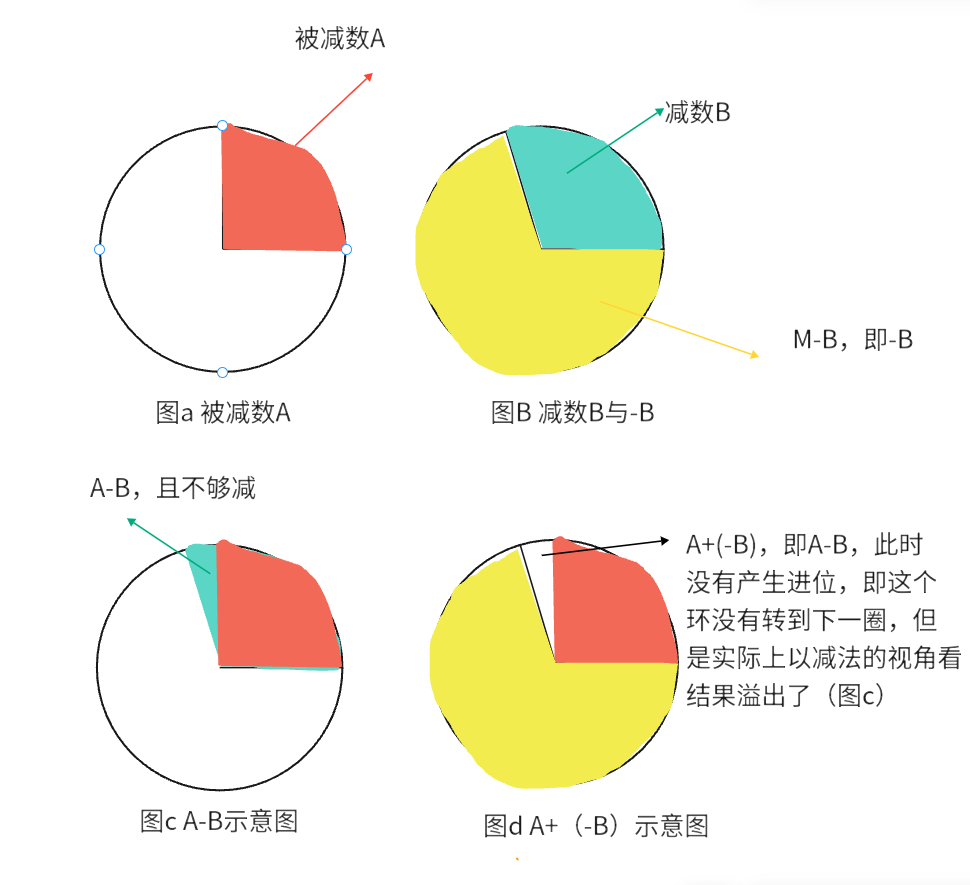
        从上图易看出无符号数减法发生溢出时，Cn=0，又已知C0=1，所以CF的值等于Cn异或C0。

二数比较方法

无符号数

        设结果为A-B，易知：

        如果ZF=0，且CF=0，则A＞B；若ZF=0，且CF=1，则A<B；ZF=1，则A=B。

有符号数

        设结果为A-B，由枚举所有情况可得：

        ZF等于0，且OF异或SF=1时，A<B。