Python打卡Day20 常见的特征筛选算法
- 奇异值的应用
- 特征降维:对高维数据减小计算量、可视化
- 数据重构:比如重构信号、重构图像(可以实现有损压缩,k 越小压缩率越高,但图像质量损失越大)
- 降噪:通常噪声对应较小的奇异值。通过丢弃这些小奇异值并重构矩阵,可以达到一定程度的降噪效果。
- 推荐系统:在协同过滤算法中,用户-物品评分矩阵通常是稀疏且高维的。SVD (或其变种如 FunkSVD, SVD++) 可以用来分解这个矩阵,发现潜在因子 (latent factors),从而预测未评分的项。这里其实属于特征降维的部分。
对于任何矩阵(如结构化数据可以变为:样本*特征的矩阵,图像数据天然就是矩阵),均可做等价的奇异值SVD分解,对于分解后的矩阵,可以选取保留前K个奇异值及其对应的奇异向量,重构原始矩阵,可以通过计算Frobenius 范数相对误差来衡量原始矩阵和重构矩阵的差异。
应用:结构化数据中,将原来的m个特征降维成k个新的特征,新特征是原始特征的线性组合,捕捉了数据的主要方差信息,降维后的数据可以直接用于机器学习模型(如分类、回归),通常能提高计算效率并减少过拟合风险。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from scipy.linalg import svd
import numpy as np
import matplotlib.pyplot as plt# 加载数据集
data = pd.read_csv('heart.csv')# 提取特征和目标变量
X = data.drop('target', axis=1)
y = data['target']
# 设置 matplotlib 支持中文
plt.rcParams['font.sans-serif'] = ['WenQuanYi Zen Hei']
plt.rcParams['axes.unicode_minus'] = False
# 划分训练集、验证集和测试集 (60%-20%-20%)
X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.4, random_state=42)
X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)# 训练逻辑回归模型(未进行特征工程)
model = LogisticRegression()
model.fit(X_train, y_train)# 在验证集上进行预测
y_pred_val = model.predict(X_val)# 计算准确率(未进行特征工程)
accuracy_before = accuracy_score(y_val, y_pred_val)
print(f"特征工程前的验证集准确率: {accuracy_before}")# 记录不同k值下的准确率
k_values = range(1, X_train.shape[1] + 1)
accuracies = []
best_k = 0
best_accuracy = 0# 使用 SVD 进行特征工程,并尝试不同的k值
for k in k_values:# 对训练集进行SVD分解U, s, Vt = svd(X_train, full_matrices=False)# 将奇异值向量转换为对角矩阵S_k = np.diag(s[:k])X_train_svd = U[:, :k] @ S_k# 对验证集进行变换X_val_centered = X_val - np.mean(X_train, axis=0)X_val_svd = X_val_centered @ Vt.T[:, :k]# 训练逻辑回归模型model_svd = LogisticRegression()model_svd.fit(X_train_svd, y_train)# 在验证集上进行预测y_pred_val_svd = model_svd.predict(X_val_svd)# 计算准确率accuracy = accuracy_score(y_val, y_pred_val_svd)accuracies.append(accuracy)# 记录最佳k值if accuracy > best_accuracy:best_accuracy = accuracybest_k = k# 输出最佳k值和对应的准确率
print(f"最佳k值: {best_k}")
print(f"最佳验证集准确率: {best_accuracy}")# 使用最佳k值在测试集上评估
U, s, Vt = svd(X_train, full_matrices=False)
S_best = np.diag(s[:best_k])
X_train_svd_best = U[:, :best_k] @ S_best# 对测试集进行变换
X_test_centered = X_test - np.mean(X_train, axis=0)
X_test_svd_best = X_test_centered @ Vt.T[:, :best_k]# 训练逻辑回归模型
model_svd_best = LogisticRegression()
model_svd_best.fit(X_train_svd_best, y_train)# 在测试集上进行预测
y_pred_test_svd = model_svd_best.predict(X_test_svd_best)# 计算准确率
accuracy_test = accuracy_score(y_test, y_pred_test_svd)
print(f"特征工程后的测试集准确率: {accuracy_test}")# 可视化不同k值下的准确率变化
plt.figure(figsize=(10, 6))
plt.plot(k_values, accuracies, marker='o')
plt.axhline(y=accuracy_before, color='r', linestyle='--', label='特征工程前的准确率')
plt.axvline(x=best_k, color='g', linestyle='--', label=f'最佳k值: {best_k}')
plt.xlabel('k (保留的奇异值数量)')
plt.ylabel('验证集准确率')
plt.title('不同k值下SVD特征工程的模型性能')
plt.legend()
plt.grid(True)
plt.show()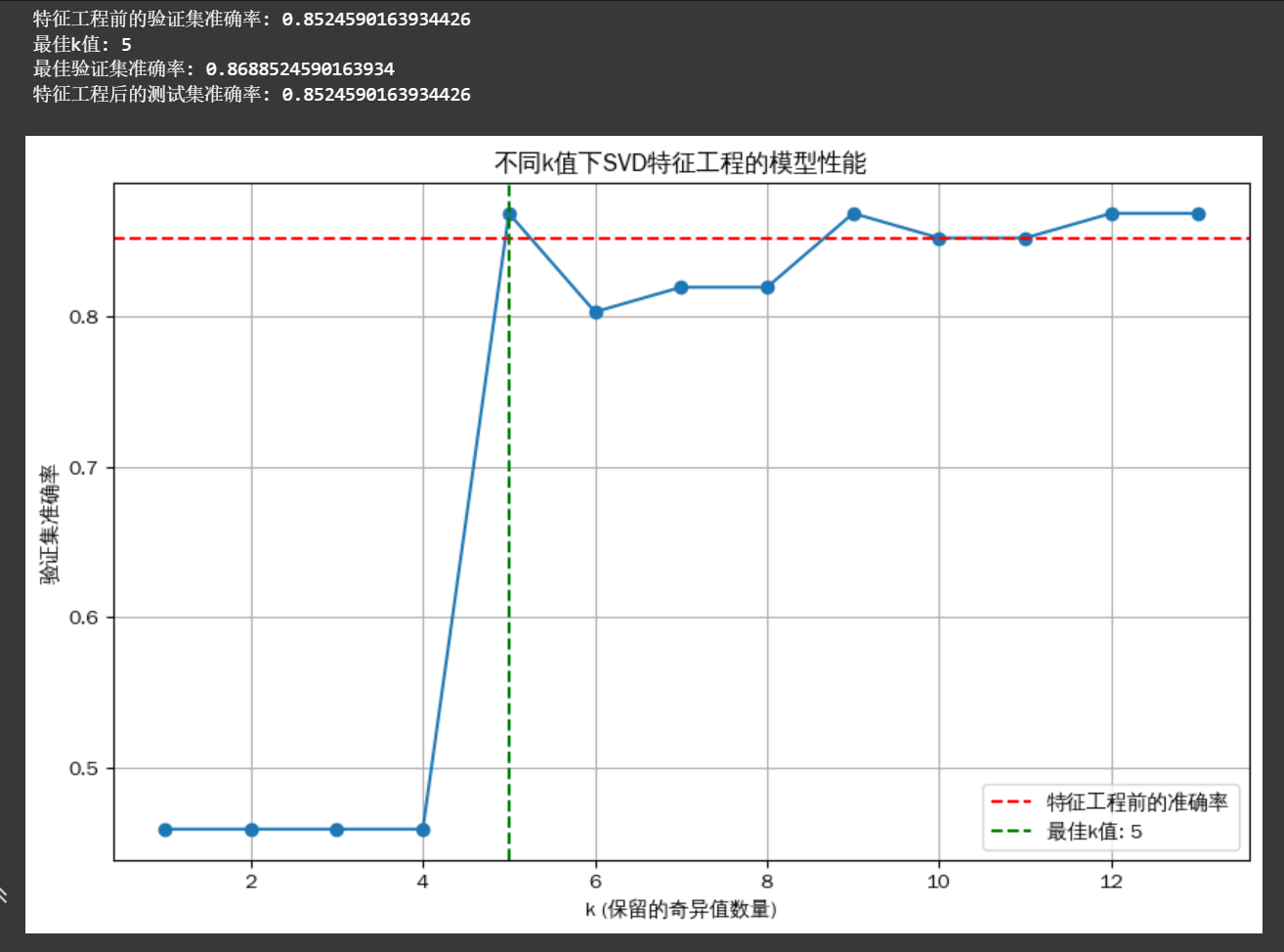
@浙大疏锦行
