CS231n-2017 Lecture4神经网络笔记
神经网络:
我们之前的线性分类器可以接受输入,进而给出评分,这是一种线性变换,再此基础上,我们对这种线性变换结果进行非线性变换,并输入到下一层线性分类器中,这个过程就像是人类大脑神经的运作一样,神经元接受信号,并输出神经递质给下一个神经元,表示是兴奋(正权重)/抑制(负权重)
激活函数:
上文提到的非线性变换,即使用激活函数,显然激活函数是非线性函数
常用的激活函数如下:
1.Sigmoid函数
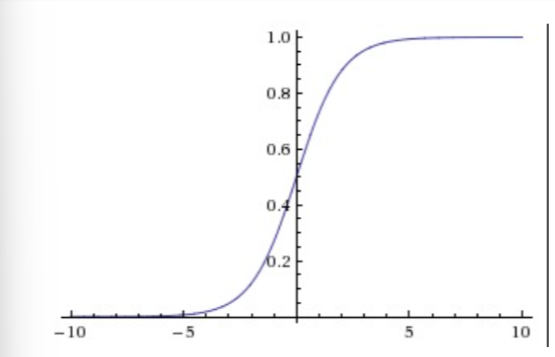
这个函数接受实数值,并将很大的负数变为0(抑制信号),很大的正数变为1(兴奋信号)
但在实际上已经很少使用,主要是因为以下两个缺点:
(1) Sigmoid函数饱和会使梯度消失
当激活函数的输出接近0或者接近1时,这里的局部梯度几乎为0,这就会导致一个问题,在反向传播的时候,我们要求的梯度会与这里的局部梯度相乘,从而导致要求的梯度为0,所谓梯度消失,则这个梯度对应的变量的信号将无法再传递
同时,为了防止这种饱和,需要在初始化权重矩阵时特别小心,否则就会导致很多神经元过饱和,神经网络无法再继续学习
(2) Sigmoid函数的输出不是以0为中心的
由于后续的神经元会以前面神经元的激活函数输出作为输入,导致其接收的输入总是正数,那么在反向传播的时候,会导致梯度要么全为正数,要么全为负数(比如对于 ,会导致
),这会导致梯度下降权重更新的时候忽然很大的正向忽然很大的负向所产生的z字形的下降。不过,在整个batch的数据的梯度被加起来后,对于权重的最终更新会有不同的正负,这样就一定程度地减轻了这个问题
2.Tanh函数
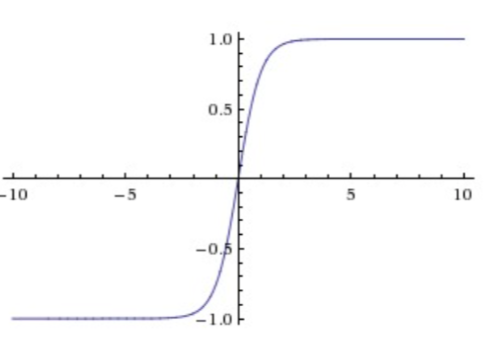
这个函数将实数值压缩到 之间
它也存在饱和问题,但和sigmoid函数不同的是,它的输出是以0为中心的
3.ReLU函数
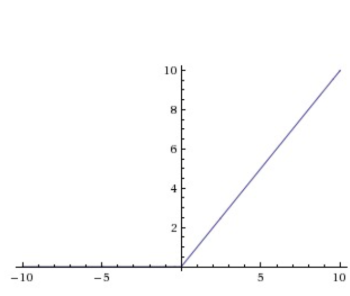
优点:
1.相较于Sigmoid和Tanh,ReLU对随机梯度下降的收敛有巨大的加速作用
2.ReLU的计算资源开销较少,只需要对矩阵进行阈值计算得到
缺点:
当很大的梯度经过ReLU的神经元时,梯度下降将x更新至负数或者接近0,那么就会损失掉这个神经元的梯度,导致其死亡
这种情况在学习率较高的时候出现频率较高,由于步长过长,导致x在一次权重更新时就下降到0
4.Leaky ReLU
为了解决ReLU的死亡问题,我们对其进行改进,使公式变为
其中 是一个小常量
5.Maxout函数
可以发现ReLU是Maxout的特殊情况,即
则Maxout拥有ReLU的所有优点,而没有其缺点
但由于的存在,它每个神经元的参数都增加了一倍
激活函数的选择问题:
通常建议使用ReLU,并注意设置学习率,监控网络中死亡神经元的比例,若死亡比例较高,则可以尝试使用Leaky ReLU或Maxout,也可以尝试tanh,但不推荐sigmoid
神经网络结构:
层状结构:
神经网络被建模成神经元的集合,神经元之间以无环图的形式连接,通常是分层的,最普通的是全连接层(fully-connected layer),全连接层中的神经元与其前后两层的神经元是完全成对连接的,但在同一个全连接层的神经元之间没有连接,如图:
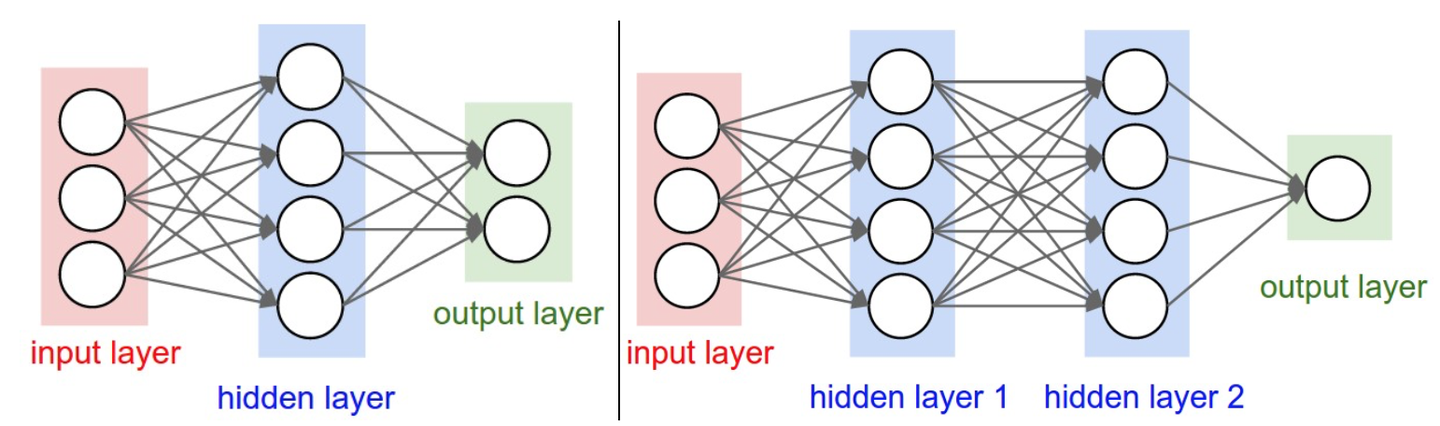
命名规则:
当我们说N层神经网络的时候,不把输入层算作一层
可使用ANN(Artificial Neural Networks)或MLP(Multi-Layer Perceptrons)来指代神经网络
输出层:
输出层通常没有激活函数
网络尺寸:
衡量神经网络尺寸的标准有两个:
1.神经元的个数
2.参数的个数
以上图举例
第一个网络有4+2=6个神经元(不算输入层), 个权重参数,还有4+2=6个偏置,共26个可学习的参数
同理,第二个网络有41个可学习的参数
神经网络前向传播计算举例:
将神经网络组成层状,会方便我们使用矩阵乘法进行前向传播,以上图右边的神经网络举例
输入是 的向量,一个层所有连接的权重可以储存在一个矩阵中,比如第一个隐藏层的权重矩阵是一个
的矩阵
, 偏置是
的向量
, 假设第一层的激活函数为f,则
即可得到第一个隐藏层的输出,后面几层的运算同理
表达能力:
可以这样来理解具有全连接层的神经网络,它们定义了一个由一系列函数组成的函数族,网络的权重就是每个函数的参数,已被证明,给出任意连续函数 和任意
,均存在至少含1个隐藏层的神经网络
, 使得
即神经网络可以近似任何连续函数
既然2层神经网络可以完美近似所有连续函数,那为什么需要将网络做得更深层呢?这是因为浅层网络实际训练效果较差
神经网络在实践中好用,是因为其表达出的函数不仅平滑,而且对于数据的统计特性有很好的拟合
但对于普通神经网络来说,层数并不是越多越好,其会面临梯度消失难以训练的问题,但对于卷积神经网络来说,层数是一个极为重要的因素,一个直观解释是,因为图像具有层次化结构,所以需要多层处理这种数据
如何设置层的数量和尺寸:
更大容量的神经网络可以表达更复杂的函数,但这既是优点也是缺点,优点是其可以分类更复杂的数据,缺点是可能造成对训练数据的过拟合
过拟合指的是网络对数据中的噪声有很强的拟合能力,而没有重视数据间的潜在基本关系(假设的),例如,下图中使用20个隐藏层的网络拟合了所有训练数据,但代价是把决策边界变成了许多不相连的红绿区域,即没有忽略异常点的噪声,而另外两个网络拟合的决策边界就较为宽泛,这样在实际测试中会有更好的泛化能力
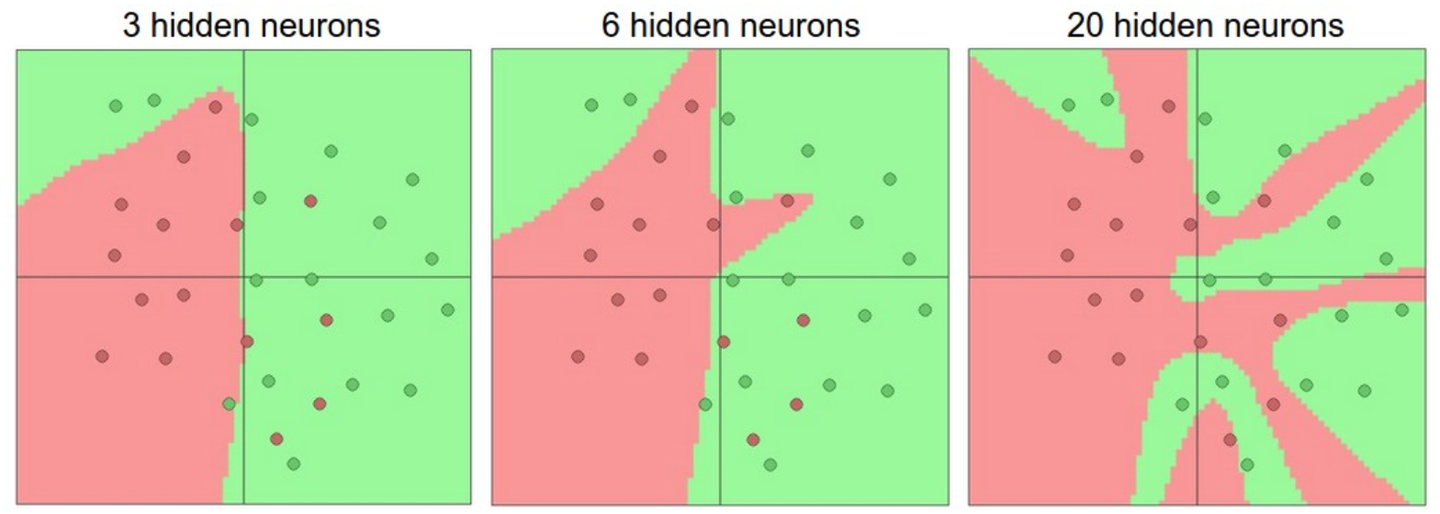
但并不是不提倡使用大容量的神经网络,小网络更难使用梯度下降等局部方法来训练,而大网络效果更好。因此我们应该想别的办法来避免过拟合,例如在Loss函数中加入正则化,下图是20隐藏层网络正则化超参数取不同值时的训练效果