当前位置： 首页 > news >正文

7月21号打卡

news 2025/7/23 15:04:09

特征降维

举个例子来说明：

PCA (无监督)：如果你有一堆人脸图片，PCA会尝试找到那些能最好地概括所有人脸变化的“主脸”（特征向量），比如脸型、鼻子大小等，它不关心这些人脸属于谁。

LDA (有监督)：如果你有一堆人脸图片，并且你知道每张图片属于哪个人（标签）。LDA会尝试找到那些能最好地区分不同人的人脸特征组合。比如，如果A和B的脸型很像，但眼睛差别很大，LDA可能会更强调眼睛的特征，即使脸型方差更大。

PCA是利用最大化方差来实现无监督降维，而LDA则是在此基础上，加入了类别信息，其优化目标就变成了类间差异最大化和类内差异最小化。

import time
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler # 特征缩放
from sklearn.decomposition import PCA # 主成分分析
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA # 线性判别分析# UMAP 需要单独安装: pip install umap-learnfrom sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix

一.PCA

n_components_pca =7
pca_manual = PCA(n_components=n_components_pca, random_state=42)X_train_pca = pca_manual.fit_transform(X_train_scaled_pca)
X_test_pca = pca_manual.transform(X_test_scaled_pca) # 使用在训练集上fit的pcaprint(f"PCA降维后，训练集形状: {X_train_pca.shape}, 测试集形状: {X_test_pca.shape}")
start_time_pca_manual = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_pca = RandomForestClassifier(random_state=42)
rf_model_pca.fit(X_train_pca, y_train)# 步骤 4: 在测试集上预测
rf_pred_pca_manual = rf_model_pca.predict(X_test_pca)
end_time_pca_manual = time.time()print(f"手动PCA降维后，训练与预测耗时: {end_time_pca_manual - start_time_pca_manual:.4f} 秒")print("\n手动 PCA + 随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred_pca_manual))
print("手动 PCA + 随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred_pca_manual))
from sklearn.svm import SVC  # 导入SVM分类器n_components_pca = 7
pca_manual = PCA(n_components=n_components_pca, random_state=42)X_train_pca = pca_manual.fit_transform(X_train_scaled_pca)
X_test_pca = pca_manual.transform(X_test_scaled_pca)print(f"PCA降维后，训练集形状: {X_train_pca.shape}, 测试集形状: {X_test_pca.shape}")
start_time_svm = time.time()
svm_model = SVC(random_state=42)  # 使用默认参数初始化SVM
svm_model.fit(X_train_pca, y_train)
svm_pred = svm_model.predict(X_test_pca)
end_time_svm = time.time()print(f"SVM训练与预测耗时: {end_time_svm - start_time_svm:.4f} 秒")print("\nPCA + SVM 在测试集上的分类报告：")
print(classification_report(y_test, svm_pred))
print("PCA + SVM 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, svm_pred))
模型准确率0 类 F1 分数1 类 F1 分数耗时（秒）
SVM0.870.860.880.0084
随机森林0.850.850.860.1650

二. t-分布随机邻域嵌入 (t-SNE) 

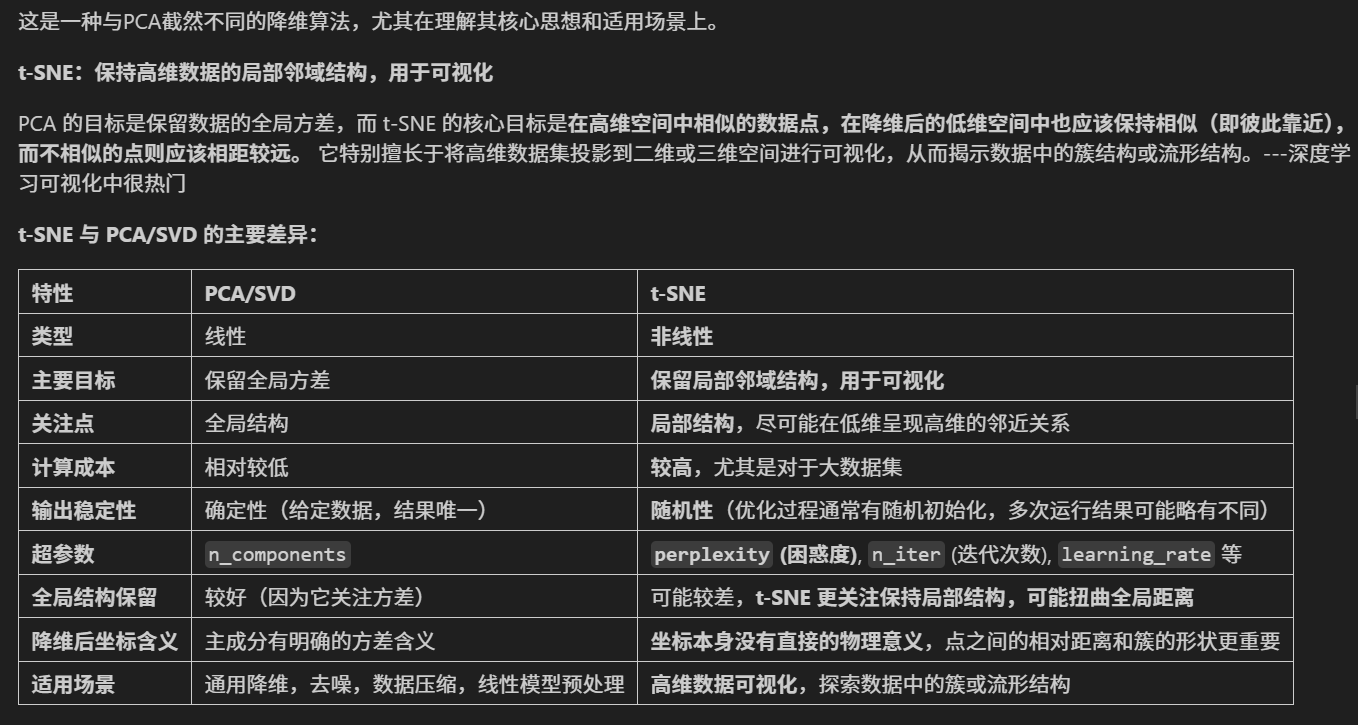
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np
import matplotlib.pyplot as plt # 用于可选的可视化
import seaborn as sns # 用于可选的可视化print(f"\n--- 3. t-SNE 降维 + 随机森林  ---")
print("       标准 t-SNE 主要用于可视化，直接用于分类器输入可能效果不佳。")# 步骤 1: 特征缩放
scaler_tsne = StandardScaler()
X_train_scaled_tsne = scaler_tsne.fit_transform(X_train)
X_test_scaled_tsne = scaler_tsne.transform(X_test) # 使用在训练集上fit的scaler# 步骤 2: t-SNE 降维
# 我们将降维到与PCA相同的维度（例如10维）或者一个适合分类的较低维度。
# t-SNE通常用于2D/3D可视化，但也可以降到更高维度。
# 然而，降到与PCA一样的维度（比如10维）对于t-SNE来说可能不是其优势所在，
# 并且计算成本会显著增加，因为高维t-SNE的优化更困难。
# 为了与PCA的 n_components=10 对比，我们这里也尝试降到10维。
# 但请注意，这可能非常耗时，且效果不一定好。
# 通常如果用t-SNE做分类的预处理（不常见），可能会选择非常低的维度（如2或3）。# n_components_tsne = 10 # 与PCA的例子保持一致，但计算量会很大
n_components_tsne =2  # 更典型的t-SNE用于分类的维度，如果想快速看到结果# 如果你想严格对比PCA的10维，可以将这里改为10，但会很慢# 对训练集进行 fit_transform
tsne_model_train = TSNE(n_components=n_components_tsne,perplexity=30,    # 常用的困惑度值n_iter=1000,      # 足够的迭代次数init='pca',       # 使用PCA初始化，通常更稳定learning_rate='auto', # 自动学习率 (sklearn >= 1.2)random_state=42,  # 保证结果可复现n_jobs=-1)        # 使用所有CPU核心
print("正在对训练集进行 t-SNE fit_transform...")
start_tsne_fit_train = time.time()
X_train_tsne = tsne_model_train.fit_transform(X_train_scaled_tsne)
end_tsne_fit_train = time.time()
print(f"训练集 t-SNE fit_transform 完成，耗时: {end_tsne_fit_train - start_tsne_fit_train:.2f} 秒")# 对测试集进行 fit_transform
# 再次强调：这是独立于训练集的变换
tsne_model_test = TSNE(n_components=n_components_tsne,perplexity=30,n_iter=1000,init='pca',learning_rate='auto',random_state=42, # 保持参数一致，但数据不同，结果也不同n_jobs=-1)
print("正在对测试集进行 t-SNE fit_transform...")
start_tsne_fit_test = time.time()
X_test_tsne = tsne_model_test.fit_transform(X_test_scaled_tsne) # 注意这里是 X_test_scaled_tsne
end_tsne_fit_test = time.time()
print(f"测试集 t-SNE fit_transform 完成，耗时: {end_tsne_fit_test - start_tsne_fit_test:.2f} 秒")print(f"t-SNE降维后，训练集形状: {X_train_tsne.shape}, 测试集形状: {X_test_tsne.shape}")start_time_tsne_rf = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_tsne = RandomForestClassifier(random_state=42)
rf_model_tsne.fit(X_train_tsne, y_train)# 步骤 4: 在测试集上预测
rf_pred_tsne_manual = rf_model_tsne.predict(X_test_tsne)
end_time_tsne_rf = time.time()print(f"t-SNE降维数据上，随机森林训练与预测耗时: {end_time_tsne_rf - start_time_tsne_rf:.4f} 秒")
total_tsne_time = (end_tsne_fit_train - start_tsne_fit_train) + \(end_tsne_fit_test - start_tsne_fit_test) + \(end_time_tsne_rf - start_time_tsne_rf)
print(f"t-SNE 总耗时 (包括两次fit_transform和RF): {total_tsne_time:.2f} 秒")print("\n手动 t-SNE + 随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred_tsne_manual))
print("手动 t-SNE + 随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred_tsne_manual))

 原始数据 → 标准化处理 → t-SNE 降维 → 随机森林训练 → 预测与评估

为什么要标准化？
t-SNE 对数据的 “尺度” 很敏感。比如一个特征的数值范围是 0-1000，另一个是 0-1，t-SNE 会更关注前者，导致结果失真。
标准化后，所有特征的均值为 0、方差为 1，保证每个特征 “公平参与”

标准 t-SNE 主要用于可视化，直接用于分类器输入可能效果不佳

代码错误在于 对测试集单独使用 t-SNE 降维，这会导致训练集和测试集的特征不兼容。正确做法是：

  1. 分类任务用 PCA/LDA 等可复用的降维方法。
  2. t-SNE 仅用于可视化，不参与模型训练。

三.线性判别分析 (LDA)

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
import time
import numpy as np
# 假设你已经导入了 matplotlib 和 seaborn 用于绘图 (如果需要)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 如果需要3D绘图
import seaborn as snsprint(f"\n--- 4. LDA 降维 + 随机森林 ---")# 步骤 1: 特征缩放
scaler_lda = StandardScaler()
X_train_scaled_lda = scaler_lda.fit_transform(X_train)
X_test_scaled_lda = scaler_lda.transform(X_test) # 使用在训练集上fit的scaler# 步骤 2: LDA 降维
n_features = X_train_scaled_lda.shape[1]
if hasattr(y_train, 'nunique'):n_classes = y_train.nunique()
elif isinstance(y_train, np.ndarray):n_classes = len(np.unique(y_train))
else:n_classes = len(set(y_train))max_lda_components = min(n_features, n_classes - 1)if max_lda_components < 1:print(f"LDA 不适用，因为类别数 ({n_classes})太少，无法产生至少1个判别组件。")X_train_lda = X_train_scaled_lda.copy() # 使用缩放后的原始特征X_test_lda = X_test_scaled_lda.copy()   # 使用缩放后的原始特征actual_n_components_lda = n_featuresprint("将使用缩放后的原始特征进行后续操作。")
else:# 实际使用的组件数不能超过LDA的上限，也不能超过我们的目标（如果目标更小）actual_n_components_lda = min(n_components_lda_target, max_lda_components)if actual_n_components_lda < 1: # 这种情况理论上不会发生，因为上面已经检查了 max_lda_components < 1print(f"计算得到的实际LDA组件数 ({actual_n_components_lda}) 小于1，LDA不适用。")X_train_lda = X_train_scaled_lda.copy()X_test_lda = X_test_scaled_lda.copy()actual_n_components_lda = n_featuresprint("将使用缩放后的原始特征进行后续操作。")else:print(f"原始特征数: {n_features}, 类别数: {n_classes}")print(f"LDA 最多可降至 {max_lda_components} 维。")print(f"本次 LDA 将实际降至 {actual_n_components_lda} 维。")lda_manual = LinearDiscriminantAnalysis(n_components=actual_n_components_lda, solver='svd')X_train_lda = lda_manual.fit_transform(X_train_scaled_lda, y_train)X_test_lda = lda_manual.transform(X_test_scaled_lda)print(f"LDA降维后，训练集形状: {X_train_lda.shape}, 测试集形状: {X_test_lda.shape}")start_time_lda_rf = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_lda = RandomForestClassifier(random_state=42)
rf_model_lda.fit(X_train_lda, y_train)# 步骤 4: 在测试集上预测
rf_pred_lda_manual = rf_model_lda.predict(X_test_lda)
end_time_lda_rf = time.time()print(f"LDA降维数据上，随机森林训练与预测耗时: {end_time_lda_rf - start_time_lda_rf:.4f} 秒")print("\n手动 LDA + 随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred_lda_manual))
print("手动 LDA + 随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred_lda_manual))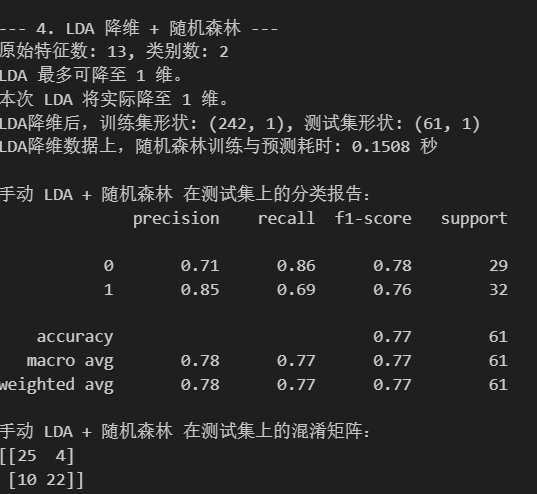

 

 

总结

一、t-SNE 的核心适用场景

仅用于可视化高维数据的分布，主要包括：

  1. 探索性数据分析：直观查看数据是否存在聚类结构（尤其在未知数据上）。
  2. 验证分类合理性：如果计划做分类，先用 t-SNE 可视化，确认数据是否可分（如果 t-SNE 都无法分开，分类器也很难）。
  3. 异常检测：在可视化中，远离簇群的点可能是异常值。
  4. 对比不同数据子集：例如，对比训练集和测试集的分布是否一致。

二、使用原则

  1. 降维维度：

    • 几乎只降到 2D 或 3D（用于平面或立体绘图）。
    • 不要尝试降到更高维度（如 10 维），这违背了 t-SNE 的设计初衷，且计算效率极低。

  2. 仅对训练集使用：

    • t-SNE 不能应用于测试集（如你之前的代码错误）。
    • 如果需要可视化测试集，应与训练集合并后一起降维（但标签分开显示）。

  3. 数据规模：

    • t-SNE 的计算复杂度极高，对大规模数据（如样本数超过 10,000），建议先使用 PCA 降维到 50 维左右，再用 t-SNE 降到 2D。

三、正确使用示例

1. 基础可视化（2D 散点图）

2. 对比不同类别的分布

3. 大规模数据优化（先 PCA 降维）

四、绝对不要做的事

  1. 不要用 t-SNE 降维后训练分类器（如你之前的代码）。
  2. 不要对测试集单独使用 t-SNE（不同数据集的 t-SNE 结果不可比）。
  3. 不要尝试将 t-SNE 结果用于预测（t-SNE 没有 “转换” 功能，只用于可视化）。

总结

t-SNE 是强大的可视化工具，但适用范围很窄。记住：只用于训练集的 2D/3D 可视化，不用于建模。如果需要降维后建模，优先使用 PCA 或其他线性方法。

@浙大疏锦行

http://www.dtcms.com/a/290961.html

相关文章：

  • 破解哈希极化：基于主动路径规划的智算网络负载均衡方案
  • Shell 编程基础入门从认识到实战
  • OSS文件上传（三）：断点续传
  • C语言关键字深度解析：从入门到精通
  • 数字ic后端设计从入门到精通12（含fusion compiler, tcl教学）全定制设计进阶
  • 【LeetCode数据结构】栈的应用——有效的括号问题详解
  • Centos安装最新docker以及ubuntu安装docker
  • ESP32-S3学习笔记＜1＞：ESP-IDF的安装与命令
  • MySQL 核心知识点梳理(2)
  • 贪心算法（基础算法）
  • 鸿蒙DevEco Studio找不到JsonFormat插件
  • 卷积神经网络中的注意力机制：CBAM详解与实践
  • 各种名词解释
  • NISP-PTE基础实操——代码审计
  • 数学建模--层次分析法
  • 17 零基础学webUI | Controlnet精讲（03）-动作姿态类控图详解
  • 孤独感和社交频率啥关系
  • 04-UE蓝图节点基本结构讲解
  • 人形机器人CMU-ASAP算法理解
  • 安全告警研判流程
  • JAVA后端开发—— JWT（JSON Web Token）实践
  • Linux system-timesyncd时间同步机制详解
  • MTSC2025参会感悟：大模型 + CV 重构全终端 UI 检测技术体系
  • 可变形卷积神经网络详解：原理、API与实战
  • 机器学习初学者理论初解
  • 深入浅出：从最小核心到完整架构，全面解析5G用户面协议栈
  • Three.js 全景图（Equirectangular Texture）教程：从加载到球面映射
  • 码分多路复用(CDM）中芯片序列正交和规格化内积的具体含义
  • 耐看点播网页入口 - 追最新电视剧，看热门电影|官网
  • 智能控制权回归：人机协创时代的极简主义编码革命