当前位置：首页 > news >正文

Datawhale 7月学习

news 2025/7/20 13:18:59

一、线性回归的意义

线性回归使理解自变量和因变量之间的关系变得简单，这使得它很重要：机器学习爱好者的起点，使理解数据变得非常简单；有助于预测分析，证明在许多行业都很有用，包括营销、金融甚至医疗保健；许多高级算法（如神经网络、逻辑回归...）的基础；计算效率很高，使其成为回归任务中使用最广泛的统计；在变量之间关系大致呈线性的任务中提供了出色的性能。

二、线性回归

线性回归：一种机器学习算法中常见的监督学习算法，用于定义因变量和对应的至少一个自变量的线性关系。这个过程是通过一条直线拟合训练数据集中真实值与相应的自变量的关系，然后可以用这一条直线可以预测之前训练数据集中没有出现过的一组自变量所对应的结果。【特别注意——这里的因变量和自变量都必须属于实数集，且自变量必须是连续的】

给定数据集D由n个 $(x_{i},y_{i})$ 组成,其中 $x_{i}=(x_{i1},x_{i2},...,x_{ik})^{T }$ k代表属性值, $y_{i}$ 表示是真实值。这里的 $x_{i}$ 表示特征矩阵， $y_{i}$ 表示为真实数值。

线性回归的表达式 $f(x_{i})=wx_{i}+b$ 。通过多次训练模型，旨在得到一个线性模型使得预测值无限逼近于真实值，即让 $f(x_{i})$ 无限接近于 $y_{i}$ 。其中 $w$ 表示模型权重(回归系数)， $b$ 表示偏差可以反映模型中未解释的数据一部分。线性回归模型中的目标函数——MSE，均方误差 $MSE=\sum_{i=1}^{n}(y_{i}-(wx_{i}+b))$

训练过程中线性回归模型如何确定模型权重和偏差？

这里采用梯度下降算法，在线性回归模型中通过随机选择数值来减少目标函数，然后不断迭代更新模型权重和偏差，直到可以把每个点的误差减少到最小值为止。

【梯度下降：通过对目标函数优化以达到最优解最小解的优化算法之一】

如果大家想理解在这个过程中两个参数更新的原理，可以看这个的详细解释梯度下降算法

借助目标函数求解在每个数据点误差的最小值情况下两个参数大小的数学原理推导(这里使用的是最小二乘法原理，即OLS原理。当然，在线性回归问题中用于求解模型的还有贝叶斯回归、最大似然估计、最小化绝对值误差)：

OLS原理是对实数集上的函数求所有参数组成矩阵 $\beta$ 的一阶偏导数，最后令这个·式子等于0就可以求出最优参数值组成的矩阵。凹凸函数可通过求二阶导数来判别:若二阶导数在区间上非负则称为凸函数;若二阶导数在区间上恒大于0,则称为严格凸函数。在这里的目标函数MSE是凸函数，所以可以用OLS原理求解。假设有 n个样本、每个样本有k个特征，模型权重为 $(w,b)^{T}$ ,数据矩阵 $X=(x_{1},1;x_{2},1;...;x_{n},1)$ ，其中 $x_{i}$ 是存储每个样本对应所有特征值的一个行向量，目标值 $y=(y_{1},y_{2},...,y_{n})^{T}$ 。

$J(\beta )=\arg min(y-X\beta )^{T}(y-X\beta)$

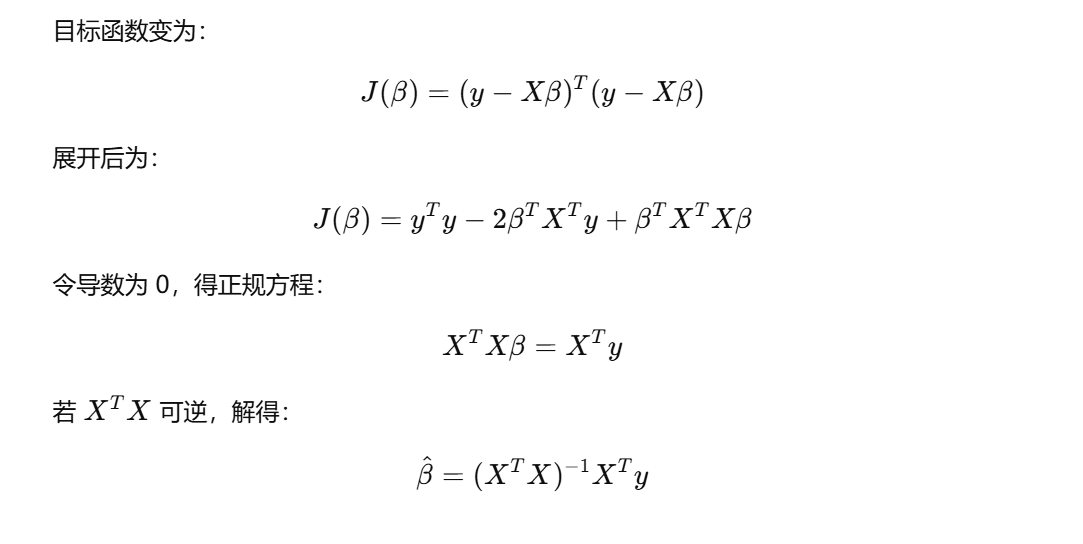
三、实际应用

线性回归模型反应两个变量之间的线性关系，可以用于预测数据。比如：预测房价变化、某种商品的价格变化、广告销售渠道预测......，为了便于理解模型建立——>参数求解——>确定线性回归表达式——>用于预测，广告销售渠道预测问题的分析(这里可以看见数据advertising)：

1、导入python库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
#导入 StatModels 库以执行线性回归
import statsmodels.api as sm
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
import warnings 
warnings.filterwarnings('ignore')  #有助于抑制不必要的警告

2、加载数据集

#把数据导入DataFrame,以表格的形式存储相应的数据
advertising = pd.read_csv( "advertising.csv" )
advertising.head()

3、可视化数据

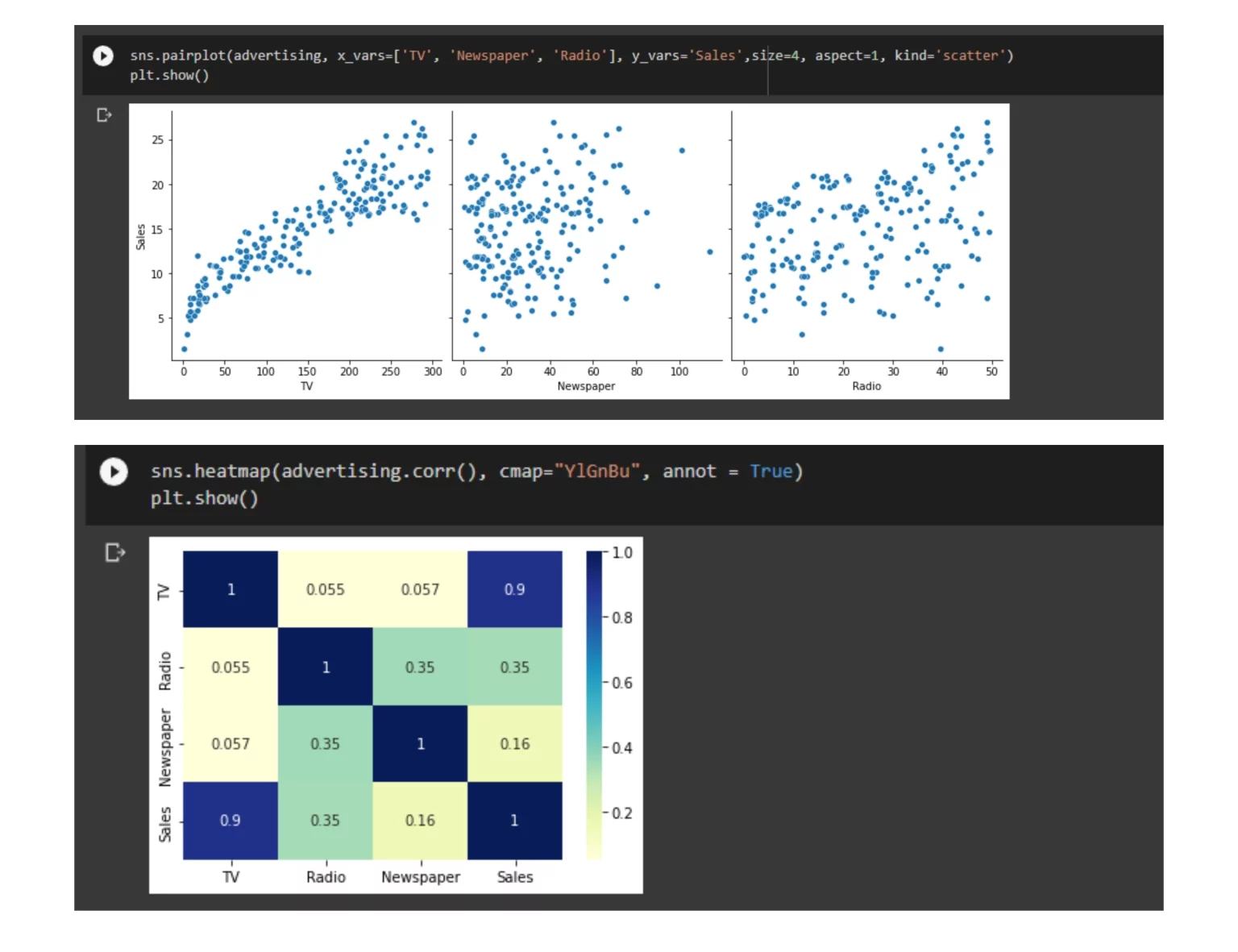
让我们在单个图中绘制目标变量与预测变量的散点图，以获得直觉。此外，为所有变量绘制热图，从散点图和热图中，我们可以观察到“销售”和“电视”与其他产品相比具有更高的相关性，因为它在散点图中显示线性模式并给出 0.9 的相关性。

sns.pairplot(advertising, x_vars=[ 'TV', ' Newspaper.,'Radio' ], y_vars = 'Sales', size = 4, kind = 'scatter' )
plt.show()
sns.heamap( advertising.corr(), cmap = 'YlGnBl', annot = True )
plt.show()

4、执行简单线性回归

在这里，由于 TV 和 Sales 具有更高的相关性，我们将对这些变量执行简单线性回归。我们可以使用 sklearn 或 statsmodels 来应用线性回归。所以我们将继续使用statmodels。在这种情况下，我们首先将特征变量“TV”分配给变量“X”，将响应变量“Sales”分配给变量“y”。库在数据集上拟合一条穿过原点的线。但为了进行拦截，需要手动使用的属性。将常量添加到数据集后，可以继续使用（普通最小二乘法）的属性拟合回归线

X = advertising[ 'TV' ]
y = advertising[ 'Sales' ]
#划分数据集
X_train, X_test, y_train, y_test = train_test_split( X, y, train_size = 0.7, test_size = 0.3, random_state = 100 )
"""
可以使用以下代码检查训练集和测试集的形状
print( X_train.shape )
print( X_test.shape )
print( y_train.shape )
print( y_test.shape )"""#常量添加到数据集后面
X_train_sm = sm.add_constant(X_train)
#使用'OLS'
lr = sm.OLS(y_train, X_train_sm).fit()print(lr.params)  #查看模型权重和偏差大小#现在，让我们看看这个线性回归作的评估指标
print(lr.summary())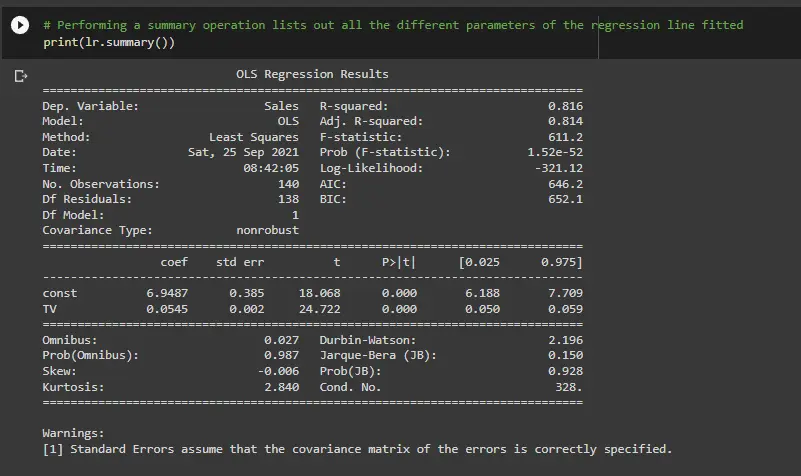

此代码为提供了线性回归的简要摘要。以下是摘要中的一些关键统计数据：

1）、TV 的系数为 0.054，p 值非常低。该系数具有统计意义。因此，这种关联并非纯粹是偶然的。
2）、R – 平方为 0.816这意味着“Sales”中 81.6% 的方差由 “TV” 解释。这是一个不错的 R 平方值。
3）、F 统计量的 p 值非常低（实际上很低）。这意味着模型拟合在统计意义上显著，并且解释的方差并非纯粹是偶然的。

5、测试数据

为了检查测试数据对值的预测程度，我们将使用 sklearn 库检查一些评估指标。当只有一个特征时，我们需要添加一个额外的列，以便成功执行线性回归拟合。

X_test_sm = sm.add_constant(X_test)
y_pred = lr.predict(X_test_sm)
print( "RMSE: ",np.sqrt( mean_squared_error( y_test, y_pred ) )
print( "R-squared: ",r2_score( y_test, y_pred ) )
X_train_lm = X_train_lm.values.reshape(-1,1)
X_test_lm = X_test_lm.values.reshape(-1,1)
print(X_train_lm.shape)
print(X_train_lm.shape)
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit( X_train_lm , y_train_lm )
print( lr.intercept_ )
print( lr.coef_ )

查看全文

http://www.dtcms.com/a/288344.html