[每日随题11] 贪心 - 数学 - 区间DP
整体概述
- 难度:1000 →\rightarrow→ 1400 →\rightarrow→ 1600
P3918 [国家集训队] 特技飞行
-
标签:贪心
-
前置知识:无
-
难度:橙 1000
题目描述:

输入格式:

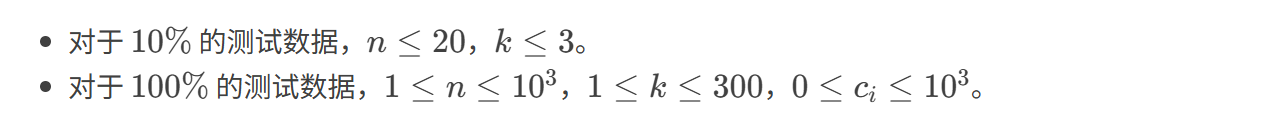
输出格式:

样例输入:
5 2
2 2
样例输出:
12
解题思路:
-
发现一次操作没有贡献,至少要两次操作。同时发现无论操作多少次,总贡献等同于只操作第一次和最后一次带来的贡献。
-
所以我们让价值最大的贡献操作时间最长即可,即将 ccc 从大到小排序,然后依次填充在头尾,模拟一遍计算总贡献即可。
完整代码
#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 1e3+5;
int n,k,a[N],c[N];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin >> n >> k;for(int i=1;i<=k;i++) cin >> c[i];sort(c+1,c+k+1,[&](int x,int y){return x>y;});int res = 0;for(int i=1,j=1;i<=k && j<=n/2;i++,j++)res += ((n-j+1) - j)*c[i];cout << res;return 0;
}
P11465 水上舞者索尼娅
-
标签:数学
-
前置知识:逆元
-
难度:黄 1400
题目描述:

输入格式:


输出格式:

样例输入:
3
2 2
3 1
12 34
样例输出:
12
14
178629506
解题思路:
-
我们发现,对于一张还剩 iii 次的 一串香蕉一串香蕉一串香蕉,在场上由 kkk 个索尼娅的时候,本质是使用了 k+1k+1k+1 张还剩 iii 次的 一串香蕉一串香蕉一串香蕉,随后产生 k+1k+1k+1 张还剩 i−1i-1i−1 次的 一串香蕉一串香蕉一串香蕉。
-
那么总使用次数即 (k+1)+(k+1)2+...+(k+1)n(k+1) + (k+1)^2 + ... + (k+1)^n(k+1)+(k+1)2+...+(k+1)n,用等比数列求和即 (k+1)∗(1−(k+1)n)1−(k+1)=(k+1)∗((k+1)n−1)k\frac {(k+1)*(1-(k+1)^n)} {1-(k+1)} = \frac {(k+1)*((k+1)^n-1)} {k}1−(k+1)(k+1)∗(1−(k+1)n)=k(k+1)∗((k+1)n−1)。
-
注意在模意义下除 kkk 是乘以 kkk 的逆元即可,
完整代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 1e9+7;
int n,k;
inline int qpow(int a,int b){int res = 1;for(;b;b>>=1,a=a*a%mod)if(b&1) res=res*a%mod;return res;
}
inline void solve(){cin >> n >> k;cout << ((k+1)*(qpow(k+1,n)-1))%mod*(qpow(k,mod-2))%mod << '\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int T; cin >> T;while(T--) solve();return 0;
}
P6457 [COCI 2006/2007 #5] IVANA
-
标签:区间DP
-
前置知识:拆环成链
-
难度:绿 1800
题目描述:

输入格式:

输出格式:

样例输入:
3
3 1 5
4
1 2 3 4
8
4 10 5 2 9 8 1 7
样例输出:
3
2
5
解题思路:
-
首先发现是环上的操作,我们先翻个倍拆环成链。
-
由于每次操作都是在已选择的区间的边缘上进行操作,我们考虑区间 DPDPDP,题目所求的是奇数个数更多的玩家获胜,那么我们定义 dpi,jdp_{i,j}dpi,j 表示当前先手取完区间 [i,j][i,j][i,j] 此时先手最多比后手多几个奇数。
-
那么 dpi,j=max(dpi,i−dpi+1,j,dpj,j−dpi,j−1)dp_{i,j} = max(dp_{i,i}-dp_{i+1,j},dp_{j,j}-dp_{i,j-1})dpi,j=max(dpi,i−dpi+1,j,dpj,j−dpi,j−1),全部更新一遍即可。
-
最后统计的时候需要注意,我们需要枚举先手取的起始点 iii,若 dpi,i−dpi+1,i+n−1>0dp_{i,i} - dp_{i+1,i+n-1} \gt 0dpi,i−dpi+1,i+n−1>0 则满足题意则统计答案。
完整代码
#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 205;
int n,m,a[N],dp[N][N];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin >> n; m = n*2;for(int i=1;i<=n;i++) cin >> a[i], a[i+n] = a[i];for(int l=1;l<=m;l++) if(a[l]&1) dp[l][l] = 1;for(int len=2;len<=n;len++){for(int l=1;l<=m-len+1;l++){int r = l+len-1;dp[l][r] = max(dp[l][l]-dp[l+1][r],dp[r][r]-dp[l][r-1]);}}int res = 0;for(int i=1;i<=n;i++) if(dp[i][i] - dp[i+1][i+n-1] > 0) res += 1;cout << res;return 0;
}
