【算法训练营Day13】二叉树part3

平衡二叉树

题目链接：110. 平衡二叉树

平衡二叉树的定义：该二叉树的所有节点的左右子树高度差不大于1

解题逻辑：

这个题和我们前一篇文章说的二叉树的高度是有关的，那么我们是否可以考虑复用求二叉树高度的代码？

一个最主要的问题就是求高度的方法返回值是int类型的，而我们判断二叉树是否平衡肯定是想返回boolean，那么我们可以考虑使用-1当作信号，正常的返回大于等于0的数字代表高度，而如果返回的是-1就说明该节点已经不平衡了。

接下来从递归三部曲来进行分析：

• 方法的参数以及返回值： 参数仍然是节点，返回值为int
• 递归出口：当前节点为null的时候，直接返回0
• 每层递归的逻辑：沿用后序遍历，在拿到左右节点的高度之后，进行如下判断
  • 如果有任意一个高度为-1，那么直接返回-1
  • 如果高度差绝对值小于等于1,则取两者较大值 + 1返回
  • 如果高度差绝对值大于1则返回-1

代码如下：

class Solution {public boolean isBalanced(TreeNode root) {int result = getHeight(root);if (result == -1) return false;return true;}public int getHeight(TreeNode node){if(node == null) return 0;int height1 = getHeight(node.left);if(height1 == -1) return -1;int height2 = getHeight(node.right);if(height2 == -1) return -1;int result = Math.abs(height1 - height2);if(result > 1) return -1;return Math.max(height1, height2) + 1;}
}

二叉树的所有路径

题目链接：257. 二叉树的所有路径

本题我们既然要记录路径，例如：

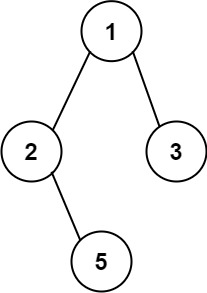
该二叉树的两条路径就是：

• 1 -> 2 -> 5
• 1 -> 3

要达到从根节点一步步指向叶子节点的效果很显然要使用前序遍历（中左右），而光使用前序遍历还是不够的，因为有些元素存在于多条路径之中。要想实现这种效果就需要使用到回溯算法，对节点遍历完之后进行回退操作。

接下来从递归三部曲分析：

• 参数与返回值：不需要返回值，而参数的话需要有当前节点，存放当前路径的列表，存放所有路径的列表
• 递归出口：当遍历到叶子节点的时候，将要将当前路径添加到结果集中
• 单层递归逻辑：将当前节点加入到当前路径的列表
• 回溯逻辑：将节点从当前路径的列表中剔除

代码如下：

class Solution {public List<String> binaryTreePaths(TreeNode root) {Deque<Integer> path = new LinkedList<>();List<String> result = new ArrayList<>();getAllPath(root,path,result);return result;}public void getAllPath(TreeNode node,Deque<Integer> path,List<String> result) {path.add(node.val);if(node.left == null && node.right == null) {StringBuilder pathStr = new StringBuilder();for(Integer item : path) {pathStr.append("->" + item);}result.add(pathStr.substring(2));}if(node.left != null) {getAllPath(node.left,path,result);path.removeLast();}if(node.right != null) {getAllPath(node.right,path,result);path.removeLast();}}
}

左叶子之和

题目链接：404. 左叶子之和

解题逻辑：

本题和上一题的逻辑很相似，也是使用回溯算法。唯一需要注意的点就是在哪里回溯？

因为本题是求所有左子叶之和，所以在选用前序遍历的情况下（中左右），那么在左之后进行回溯即可。

代码如下：

class Solution {public int sumOfLeftLeaves(TreeNode root) {List<Integer> add = new ArrayList<>();getLeftAdd(root,add);int count = 0;for(Integer item : add) {count += item;}return count;}public void getLeftAdd(TreeNode node,List<Integer> add) {if(node == null) return ; getLeftAdd(node.left,add);if(node.left != null && node.left.left == null && node.left.right == null) add.add(node.left.val);     getLeftAdd(node.right,add);}}

完全二叉树的节点个数

题目链接：222. 完全二叉树的节点个数

任选一个遍历方法直接计数就行：

class Solution {public int countNodes(TreeNode root) {CountHelper countHelper = new CountHelper();preRead(root,countHelper);return countHelper.count;}public void preRead(TreeNode node,CountHelper countHelper){if(node == null) return;countHelper.count++;preRead(node.left,countHelper);preRead(node.right,countHelper);}class CountHelper{int count = 0;}}