当前位置：首页 > news >正文

7.16 拓扑排序 | 欧拉回路 |链表排序前缀和

news 2025/7/17 9:37:33

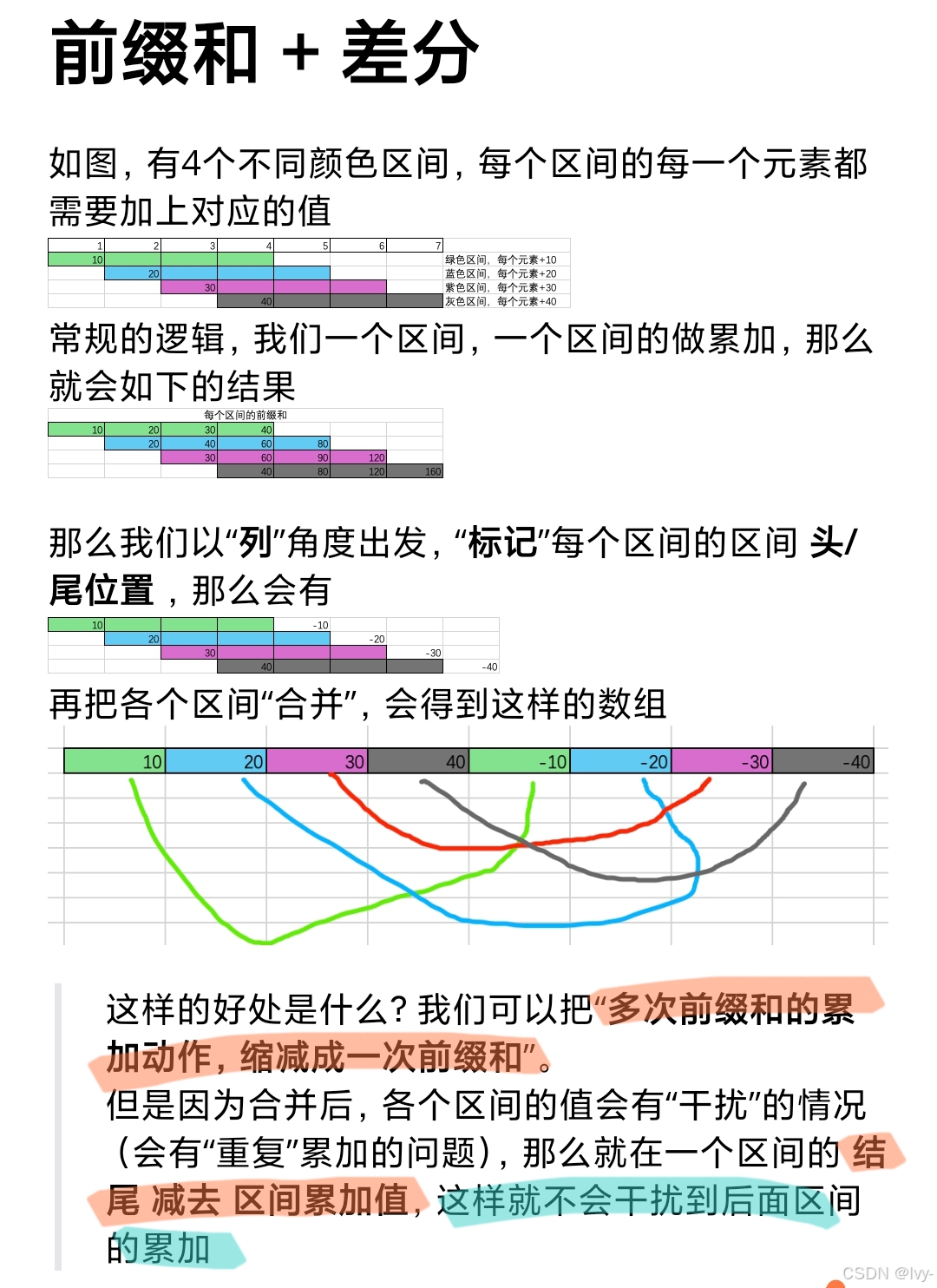
lc1109.前缀和
res[book[0] - 1] += book[2], res[book[1]] -= book[2];
多开一块，记录和上一个的变化后，来累加
res[i] += res[i - 1];

暴力tle

class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n)
{
vector<int> ret(n,0);
for(auto& b:bookings)
{
for(int i=b[0];i<=b[1];i++)
{
ret[i-1]+=b[2];
}
}
return ret;
}
};

class Solution {

public:

vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {

vector<int> res(n+1, 0);

for (auto& book : bookings)

res[book[0] - 1] += book[2], res[book[1]] -= book[2];

res.pop_back();

//多开一块，记录和上一个的变化

for (int i = 1; i < n; ++i)

res[i] += res[i - 1];

return res;

}

};

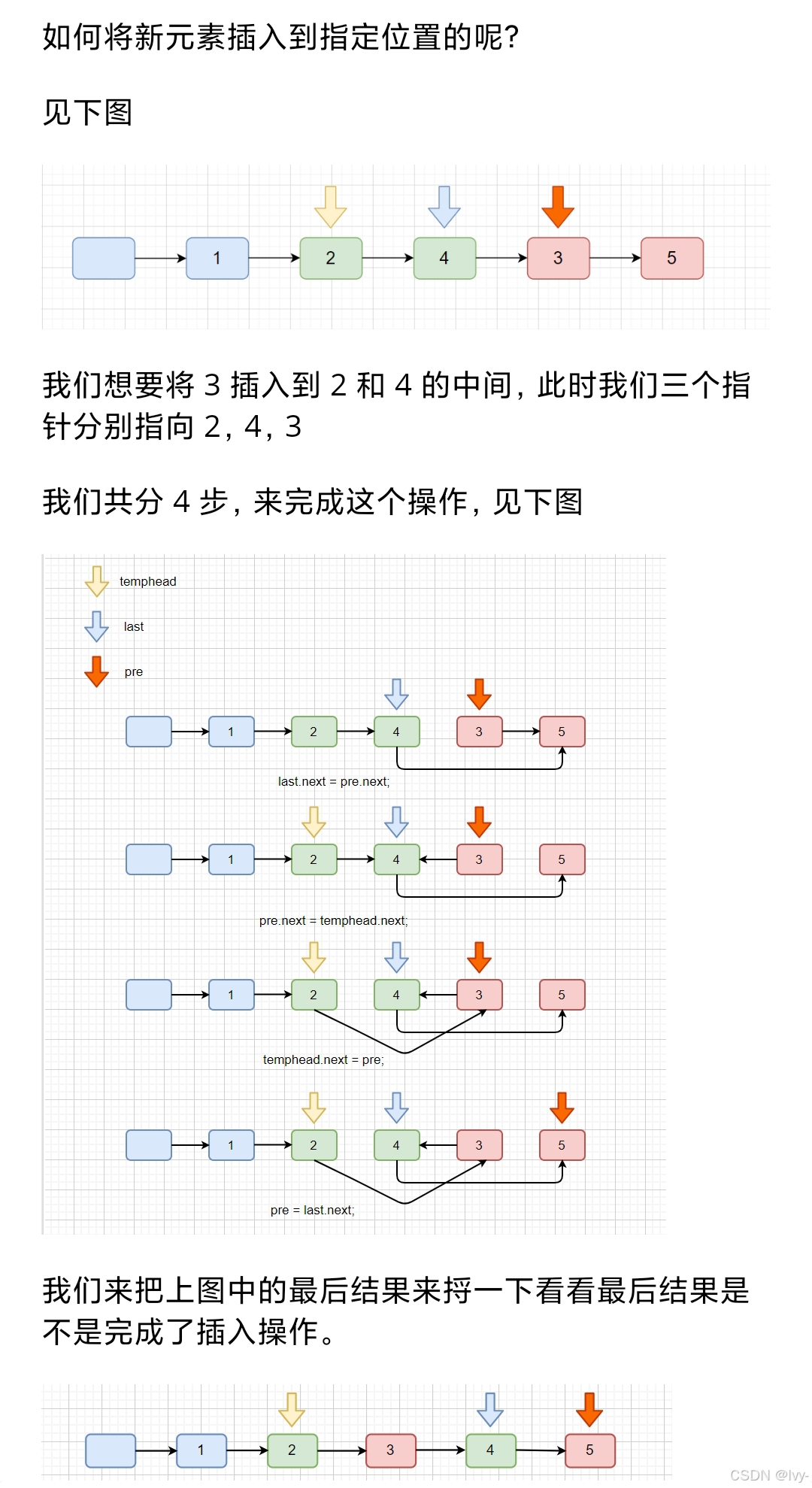
lc147.链表插入排序

lc2065.含返回&限制的最大价值和

class Solution {
public:
int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int max_time) {
int n = values.size();
vector<vector<pair<int, int>>> g(n);
for (auto& e : edges) {
int x = e[0], y = e[1], t = e[2];
g[x].emplace_back(y, t);
g[y].emplace_back(x, t);
}

int ans = 0;
vector<int> vis(n);
vis[0] = true;
auto dfs = [&](auto&& dfs, int x, int sum_time, int sum_value) -> void

{
if (x == 0) {
ans = max(ans, sum_value);
// 注意这里没有 return，还可以继续走
}
for (auto& [y, t] : g[x]) {
if (sum_time + t > max_time) {
continue;
}
if (vis[y]) {
dfs(dfs, y, sum_time + t, sum_value);
} else {
vis[y] = true;
// 每个节点的价值至多算入价值总和中一次
dfs(dfs, y, sum_time + t, sum_value + values[y]);
vis[y] = false; // 恢复现场
}
}
};
dfs(dfs, 0, 0, values[0]);
return ans;
}
};

欧拉回路

lc753.欧拉回路-破解密码箱

能从图中一点出发，不重复地走完所有边，最后回到起点的路径，就是欧拉回路。

每个点的入度==出度，则定为欧拉图

用深度优先搜索（DFS）结合集合去重，构造出满足条件的字符串：

#include <iostream>
#include <string>
#include <unordered_set>
using namespace std;

class Solution {
public:
string crackSafe(int n, int k) {
// n 为 1 时，直接返回 0 到 k - 1 拼接的字符串
if (n == 1) {
string res;
for (int i = 0; i < k; ++i) {
res += to_string(i);
}
return res;
}
unordered_set<string> S; // 用于记录已经用过的 n 长度（或相关）的子串，避免重复走
string ans; // 存储最终要返回的结果字符串
int m = pow(k, n) + n - 1; // 计算结果字符串的总长度

// 定义深度优先搜索函数，参数 a 是当前已经构造的字符串
function<void(string)> dfs = [&](string a) {
if (a.size() == m) { // 如果当前构造的字符串长度达到了目标长度
ans = a; // 把当前字符串赋值给结果
return;
}
// 取当前字符串的后 n - 1 个字符，作为下一次拼接的基础
string o = a.substr(a.size() - (n - 1), n - 1);
for (int i = 0; i < k; ++i) { // 尝试拼接 0 到 k - 1 这些数字
string s = o + to_string(i);
if (S.find(s) == S.end()) { // 如果这个拼接后的子串没在集合里，说明没走过
S.insert(s); // 标记为已走过
dfs(a + to_string(i)); // 继续往下构造字符串
S.erase(s); // 回溯，把标记去掉，尝试其他可能
if (!ans.empty()) { // 如果已经找到结果了，就直接返回，不用再搜了
return;
}
}
}
};

dfs(string(n - 1, '0')); // 初始字符串用 n - 1 个 '0' 开头，开始深度优先搜索
return ans;
}
};

解释

1. 整体功能：
要生成一个特殊字符串，这个字符串能包含所有由 n  位、每位取值是 0  到 k - 1  组成的不同“片段” 。打个比方， n = 2 ， k = 2  时，要涵盖 00 、 01 、 10 、 11  这些两位的组合情况，最终构造出一个把这些片段按规则串起来的长字符串。
2. 特殊情况处理（ n == 1 ）：
如果 n  是 1  ，那直接把 0  到 k - 1  这些数字转成字符拼接起来返回就行。比如 k = 3  ， n = 1  时，就返回 "012"  。
3. 核心逻辑（深度优先搜索 dfs  ）：
- 参数与终止条件： dfs  函数参数 a  是当前已经构造出的字符串。当 a  的长度达到 m （前面计算好的目标总长度），就把 a  赋值给 ans  ，结束当前这条搜索路径。
- 子串截取（ o  的作用）：每次从当前字符串 a  的末尾取 n - 1  个字符作为 o  。这 n - 1  个字符是为了和后面要拼接的数字 i  组成一个新的、长度可能符合我们要去重判断的子串（用来保证每个 n  位的片段只出现一次）。
- 尝试拼接与去重：循环 i  从 0  到 k - 1  ，把 o  和 i  转成的字符拼接成 s  。用集合 S  检查 s  有没有出现过，没出现过就标记（插入集合）、接着递归调用 dfs  往下构造字符串，递归返回后再回溯（从集合移除 s  ）。一旦 ans  被赋值了（找到结果了），就直接返回，停止继续搜索。
- 初始调用：最开始调用 dfs  时，用 n - 1  个 '0'  组成的字符串开头，启动整个深度优先搜索的过程，去尝试构造出符合要求的长字符串。

这样通过深度优先搜索不断尝试拼接数字，结合集合去重，就能构造出涵盖所有 n  位 k  进制组合片段的结果字符串啦

lc3243
优化方向：图的dp

class Solution {
public:
vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
vector<vector<int>> g(n - 1);
for (int i = 0; i < n - 1; i++) {
g[i].push_back(i + 1);
}
vector<int> vis(n - 1, -1);

auto bfs = [&](int i) -> int {
vector<int> q = {0};
for (int step = 1; ; step++) {
vector<int> nxt;
for (int x : q) {
for (int y : g[x]) {
if (y == n - 1) {
return step;
}
if (vis[y] != i) {
vis[y] = i;
nxt.push_back(y);
}
}
}
q = move(nxt);
}
};

vector<int> ans(queries.size());
for (int i = 0; i < queries.size(); i++) {
g[queries[i][0]].push_back(queries[i][1]);
ans[i] = bfs(i);
}
return ans;
}
};

图的dp

class Solution {

public:

vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {

vector<vector<int>> from(n);

vector<int> f(n);

iota(f.begin(), f.end(), 0);

vector<int> ans(queries.size());

for (int qi = 0; qi < queries.size(); qi++) {

int l = queries[qi][0], r = queries[qi][1];

from[r].push_back(l);

if (f[l] + 1 < f[r]) {

f[r] = f[l] + 1;

for (int i = r + 1; i < n; i++) {

f[i] = min(f[i], f[i - 1] + 1);

for (int j : from[i]) {

f[i] = min(f[i], f[j] + 1);

}

ans[qi] = f[n - 1];

}

return ans;

}

};

lcr113

解决“课程安排”问题的，简单说就是找一个合理的上课顺序，满足先修课要求。

核心思路

用“拓扑排序”的方法：先上没有先修课的，上完一门课后，把它的后续课程的先修要求减一，直到所有课都排好，或者发现排不了（有循环依赖）。

步骤拆解

1. 建图和统计先修课数量：
- 用 graph 记录每个课程的后续课程（比如上完课A才能上B，就记A→B）。
- 用 inDegress 记录每个课程需要的先修课数量（比如B需要1门先修课A，就记为1）。
2. 找起点：
- 把所有没有先修课（ inDegress 为0）的课程放进队列，这些是可以先上的。
3. 按顺序选课：
- 从队列里选一门课，放进结果列表。
- 这门课的后续课程，先修课数量减一（因为这门课已经上完了）。
- 如果某后续课程的先修课数量变成0，就把它放进队列，接下来可以上。
4. 检查结果：
- 如果结果里的课程数量等于总课程数，说明能排好，返回结果。
- 否则说明有循环依赖（比如A要先上B，B要先上A），返回空列表。

比如有3门课，要求先上0才能上1，先上0才能上2，那代码会返回 [0,1,2] 或 [0,2,1] ，都是合理的顺序。

class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
unordered_map<int, vector<int>> graph;
vector<int> inDegress(numCourses, 0);
for (auto& pre : prerequisites) {
graph[pre[1]].push_back(pre[0]);
inDegress[pre[0]]++;
}

vector<int> ret;
queue<int> que;
for (int i = 0; i < inDegress.size(); ++i) {
if (inDegress[i] == 0) {
que.push(i);
}
}

while (!que.empty()) {
int node = que.front();
que.pop();
ret.push_back(node);
for (auto& n : graph[node]) {
inDegress[n]--;
if (inDegress[n] == 0) {
que.push(n);
}
}
}

if (ret.size() != numCourses) {
return {};
}
return ret;
}
};

子序列dp

lc3202
利用取余后，交替出现的性质

“找出整数数组 nums 中最长有效子序列长度”问题的

1. 整体思路

要找满足条件的最长子序列，条件是子序列中相邻两个数的和对 k 取余的结果都相等。

代码通过动态规划的思路，用一个二维数组 f 来记录状态，逐步更新并找到最长有效子序列的长度。

2. 变量和数组含义

- ans ：用来保存最终找到的最长有效子序列的长度，初始为 0 。

- f ：是一个 k×k 的二维数组， f[a][b] 可以理解为：以对 k 取余后结果为 a 的数开头，接着一个对 k 取余后结果为 b 的数时，能形成的有效子序列的长度。

3. 循环过程

- 外层循环（遍历 nums 数组）：

每次取出数组里的一个数 x ，先把 x 对 k 取余（因为我们关心的是和对 k 取余的结果，取余后计算更方便）。

- 内层循环（遍历 0 到 k - 1 ）：

对于当前取余后的 x ，遍历 y （ y 从 0 到 k - 1 ）。 f[y][x] = f[x][y] + 1 这一步是核心：

- 可以想象成，之前有以 x 开头、 y 接着的情况（对应 f[x][y] ），现在反过来，以 y 开头、 x 接着，就能形成新的序列，长度就是之前 f[x][y] 的长度加 1 。

- 然后用 f[y][x] 去更新 ans ，保证 ans 始终是当前找到的最长有效子序列长度。

4. 举个简单例子辅助理解

比如 nums = [1,2,3] ， k = 2 ：

- 处理 x = 1 （ 1 % 2 = 1 ）：

内层循环 y 从 0 到 1 。此时 f 里的值都是初始的 0 ，所以 f[0][1] = f[1][0] + 1 = 0 + 1 = 1 ， f[1][1] = f[1][1] + 1 = 0 + 1 = 1 ，然后 ans 会被更新为 1 。

- 处理 x = 2 （ 2 % 2 = 0 ）：

内层循环 y 从 0 到 1 。当 y = 0 时， f[0][0] = f[0][0] + 1 = 0 + 1 = 1 ；当 y = 1 时， f[1][0] = f[0][1] + 1 = 1 + 1 = 2 ，这时候 ans 会被更新为 2 。

- 后续再继续处理 x = 3 （ 3 % 2 = 1 ），不断更新 f 和 ans ，最终得到最长有效子序列的长度。

简单来说，代码就是利用二维数组 f 记录不同余数开头和接着的序列长度情况，通过不断遍历数组元素，更新这些状态，从而找到最长有效子序列的长度，巧妙地利用动态规划思路解决了问题。不过要注意，这种实现背后的数学逻辑是基于子序列相邻和取余相等的条件，通过这样的状态转移来覆盖可能的有效子序列情况。