[NOIP][C++] 树的重心

树的重心

定义

对于一个树，树的重心定义为：删掉某点 i 后，若剩余 k 个连通分量，那么定义 d(i) 为这些连通分量中点的个数的最大值，所谓重心，就是使得 d(i) 最小的点 i。

基于以上定义，一个树的重心可能会有一个或者两个。

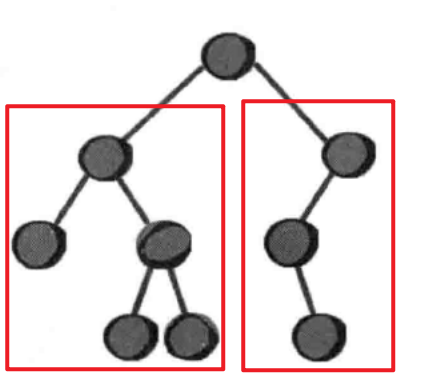
如图所示，这棵树无点权、无边权、无向。
假设我们删掉最上面的点，剩下的2个子树大小分别为5和3，那么取较大值d(i)=5。
能够使 d(i) 最小的点，则为重心。

求法

dfs求重心代码：（C++）

#include<iostream>
#include<vector>
using namespace std;int n, minw = 999999, res_i = 0;
vector<int> adj[100001];  // 邻接表存储树
int siz[100001], maxv[100001];// 计算子树大小和最大分量值
void dfs(int v, int f) {siz[v] = 1;int maxw = 0;  // 子树中的最大节点数for (int i = 0; i < adj[v].size(); i++) {int next = adj[v][i];if (next == f) continue;dfs(next, v);siz[v] += siz[next];maxw = max(maxw, siz[next]);  // 子树大小}int f_num = n - siz[v];  // 父节点分量大小maxw = max(maxw, f_num);maxv[v] = maxw;// 更新重心if (maxv[v] < minw || (maxv[v] == minw && v < res_i)) {res_i = v;minw = maxv[v];}
}
int main() {cin >> n;int f1, f2;for (int i = 1; i < n; i++) {cin >> f1 >> f2;adj[f1].push_back(f2);  // 邻接表存边（双向）adj[f2].push_back(f1);}dfs(1, 0);cout << res_i << endl;return 0;
}

输入输出样例 #1

输入 #1

4
1 2 
2 3 
3 4

输出 #1

2