2025 XYD Summer Camp 7.14 模考

时间

• 8:30 开 T1 稍微推了推做出来了，过样例之后开始看 T2
• 想了一会儿推了一个计算答案的式子，写完之后发现错了
• 9:00 手模一下发现式子错完了
• 9:40 终于把正确的式子推好了
• 10:00 过了大样例
• T3 联想到一个 trick 秒了，10:30 写完 spj 过了大样例
• 然后一直在做 T4，30 分暴力写完了之后又把特殊性质那一档码完了，可惜最后 10min 没调出来
• 笑点解析：结束前 2min 发现 T1 假了，只能祈祷不要挂太多分

成绩

题解 & 错因

T1

给定一个长度为 $n$ 的序列 $a$，要求构造一个 $01$ 数组 $b$，满足：
$$b_i=\{\begin{array}{cc}0& \text{if }{\sum }_{j=1}^{i-1}{b}_i\le a_i\\ 1& \text{if }{\sum }_{j=1}^{i-1}{b}_i=a_i\end{array}$$
求 ${\sum }_{i=1}^n{b}_i$ 的最大值。

$1\le n\le 2\times 10^5$，

首先考虑 $b_i=1$ 的位置的 $a_i$ 一定形如 $0,1,2,\cdots$ 这样的序列，因此 $\forall a_i=a_j,i<j$ 只有 $b_j$ 可能为 $1$。在这些可能的位置上贪心填 $1$ 即可。

• 错因：当 $b_i=0$ 的时候直接把限制扔了。

#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 2e5 + 5;
int n, a[maxn], pos[maxn];
bool MemoryED; int main() {scanf("%d", &n);for (int i = 1; i <= n; i ++)scanf("%d", &a[i]);for (int i = 1; i <= n; i ++)if (i > pos[a[i]]) pos[a[i]] = i;int ans = 0;for (int i = 1; i <= n; i ++)if (i == pos[a[i]] && ans == a[i]) ans ++;printf("%d\n", ans);return 0;
}

T2

给定 $n,c$，求所有长度为 $n$ 的正整数序列 $a$，满足 $a$ 中所有元素不超过 $c$，且 $a_i$ 是 $a_{i+1}$ 的倍数（也可以相等）。

$1\le n,c\le 5\times 10^7$。

考虑枚举 $a_n$ 即最大的数，先筛出 $5\times 10^7$ 以内的质数，用 dfs 枚举每个质数的次数就可以同时维护出 $a_n$ 质因数分解的结果。现在的限制就是 $\forall i\in [1,n-1]$，$a_i$ 质因数分解后，每个质因子的次数不超过 $a_{i+1}$ 的质因子次数，相当于对于 $a_n$ 的每个质因子的指数，进行 $n-1$ 轮操作，每次减去非负整数，求最后指数非负的方案数，可以用 xtr 寒假讲的一个套路直接用组合数算答案（预处理阶乘逆元后 $O(1)$ 回答）；注意到不同质因子贡献是独立的，整个的答案只要简单乘起来即可。时间复杂度 $O(n+c)$。

#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0) << "KB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 5e7 + 55, P = 998244353;
const int B = 5e7 + 50;
int n, lim;
int p[maxn >> 2], cnt = 0; bool vis[maxn];
int fac[maxn], inv[maxn];
namespace ModOptions_normal {int add(int x, int y) { return (x + y) % P; } void addto(int &x, int y) { (x += y) %= P; }int mul(int x, int y) { return 1ll * x * y % P; } void multo(int &x, int y) { x = mul(x, y); }int qp(int x, int y) {int res = 1; for (; y; y >>= 1, multo(x, x))if (y & 1) multo(res, x);return res;} int divv(int x, int y) { return 1ll * x * qp(y, P - 2) % P; } void divto(int &x, int y) { x = divv(x, y); } int sub(int x, int y) { return (x + P - y) % P; } void subto(int &x, int y) { x = sub(x, y); }
} using namespace ModOptions_normal;
void init() {for (int i = 2; i <= 5e7; i ++) {if (!vis[i]) p[++ cnt] = i;for (int j = 1; 1ll * i * p[j] <= 5e7 && j <= cnt; j ++) {vis[i * p[j]] = 1;if (i % p[j] == 0) break;}} fac[0] = inv[0] = 1;for (int i = 1; i <= B; i ++) fac[i] = mul(fac[i - 1], i);inv[B] = divv(1, fac[B]);for (int i = B - 1; i; i --)inv[i] = mul(inv[i + 1], i + 1);
} int C(int i, int j) {if (i < j) return 0;return mul(fac[i], mul(inv[j], inv[i - j]));
} int ans = 0;
void dfs(int now, int pid, int m, int now_ans) {if (now > lim) return ;addto(ans, now_ans);if (pid > cnt) return ;for (int nxt_pid = pid; nxt_pid <= cnt; nxt_pid ++) {if (1ll * now * p[nxt_pid] > lim) break;for (int c = 1, nxt_now = now; ; c ++) {if (1ll * nxt_now * p[nxt_pid] > lim) break;nxt_now *= p[nxt_pid], dfs(nxt_now, nxt_pid + 1, m + c, mul(now_ans, C(n + c - 1, n - 1)));}}
}
bool MemoryED; int main() { // open(3);cerr << cost_space << '\n';scanf("%d %d", &n, &lim), init();dfs(1, 1, 1, 1), printf("%d\n", ans);return 0;
}

T3

给定一张 $n$ 个点 $m$ 条边的无向图，边有边权，求所有 $1$ 到 $n$ 的最短路中最大的边权极差，即对于所有最短路 $p$，求
$$\underset{e\in p}{\max }{w}_e-\underset{e\in p}{\min }{w}_e$$
的最大值。

$2\le n\le 10^5$，$1\le m\le 2\times 10^5$。保证无重边。

不妨考虑钦定最大值的边 $(u,v)$（首先显然要求这条边在一条最短路上），问题就变成求从 $1$ 到 $u$ 和从 $v$ 到 $n$ 的所有最短路中最小边权的最小值，这个直接正反两遍 dijkstra 即可。接下来貌似还要求 $(u,v)$ 得是这条拼起来的路径上边权最大的边，不过考虑若这条路径是最优解，这条路径上真正的最大边权的边也一定会拿到这条路径里算一次，也就是说 $(u,v)$ 如果不是最大边权的边，那么它的贡献就会被最大边权的边顶掉。所以直接枚举 $(u,v)$ 即可。复杂度 $O(n\log n)$。std 好像是线性的，能过就行。

#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5, maxm = 2e5 + 5;
int n, m;
struct Edge { int to, nxt, val; };
struct Graph {Edge e[maxm << 1];int head[maxn], ecnt = 1;void addEdge(int u, int v, int w) { e[++ ecnt] = Edge { v, head[u], w }, head[u] = ecnt; }
} G;
int pre_dis[maxn], pre_mn[maxn], pre[maxn];
bool vis[maxn];
priority_queue<pair<pair<int, int>, int> >q;
void pre_dijkstra() {for (int i = 1; i <= n; i ++)pre_dis[i] = pre_mn[i] = inf, vis[i] = 0;pre_dis[1] = 0, pre_mn[1] = inf, q.push(mk(mk(0, -inf), 1));while (!q.empty()) {int u = q.top().second; q.pop();if (vis[u]) continue; vis[u] = 1;for (int i = G.head[u]; i; i = G.e[i].nxt) {int v = G.e[i].to, w = G.e[i].val;if (pre_dis[v] > pre_dis[u] + 1 || (pre_dis[v] == pre_dis[u] + 1 && pre_mn[v] > min(w, pre_mn[u]))) {pre_dis[v] = pre_dis[u] + 1, pre_mn[v] = min(w, pre_mn[u]), pre[v] = u;if (!vis[v]) q.push(mk(mk(-pre_dis[v], -pre_mn[v]), v));}}}
}
int suf_dis[maxn], suf_mn[maxn], suf[maxn]; 
void suf_dijkstra() {for (int i = 1; i <= n; i ++)suf_dis[i] = suf_mn[i] = inf, vis[i] = 0;suf_dis[n] = 0, suf_mn[n] = inf, q.push(mk(mk(0, -inf), n));while (!q.empty()) {int u = q.top().second; q.pop();if (vis[u]) continue; vis[u] = 1;for (int i = G.head[u]; i; i = G.e[i].nxt) {int v = G.e[i].to, w = G.e[i].val;if (suf_dis[v] > suf_dis[u] + 1 || (suf_dis[v] == suf_dis[u] + 1 && suf_mn[v] > min(w, suf_mn[u]))) {suf_dis[v] = suf_dis[u] + 1, suf_mn[v] = min(w, suf_mn[u]), suf[v] = u;if (!vis[v]) q.push(mk(mk(-suf_dis[v], -suf_mn[v]), v));}}}
} void pre_output(int u) {if (u == 0) return ;pre_output(pre[u]), printf("%d ", u);
} void suf_output(int u) {if (u == 0) return ;printf("%d ", u), suf_output(suf[u]);
}
bool MemoryED; int main() { // open(2 copy);scanf("%d %d", &n, &m);for (int i = 1, u, v, w; i <= m; i ++)scanf("%d %d %d", &u, &v, &w), G.addEdge(u, v, w), G.addEdge(v, u, w);pre_dijkstra(), suf_dijkstra(); int ans = 0, ans_u, ans_v;for (int i = 2; i <= G.ecnt; i ++) {int u = G.e[i].to, v = G.e[i ^ 1].to;if (pre_dis[u] + suf_dis[v] + 1 > pre_dis[n]) continue;if (ans <= G.e[i].val - min(min(pre_mn[u], suf_mn[v]), G.e[i].val)) {ans = G.e[i].val - min(min(pre_mn[u], suf_mn[v]), G.e[i].val);ans_u = u, ans_v = v;}} printf("%d\n", pre_dis[n]), pre_output(ans_u), suf_output(ans_v);return 0;
}

T4

给定 $n$ 个点的二叉树，每个点 $u$ 有一个标记 xu∈{ −1,0,1 }x_u\in\set{-1,0,1}xu​∈{−1,0,1}；现在会对这棵树进行若干次遍历并生成一个序列 $p$，遍历的方法是：

• 从根节点开始，一开始 $p$ 为空；
• 假设访问到 $u$，按照其标记分类讨论：
  • $x_u=-1$，那么先在 $p$ 最后面加上 $u$，然后递归左子树，最后递归右子树。（点 $u$ 进行先序遍历）
  • $x_u=0$，那么先递归左子树，然后在 $p$ 最后面加上 $u$，最后递归右子树。（点 $u$ 进行中序遍历）
  • $x_u=1$，那么先递归左子树，然后递归右子树，最后在 $p$ 最后面加上 $u$。（点 $u$ 进行后序遍历）
• 若递归到空子树直接返回。

$Q$ 次询问，每次询问形如：

• 给定 $[l,r]$ 和一个 $x^{\prime }$，对于所有 $i\in [l,r]$ 令 $x_i\leftarrow x^{\prime }$；
• 对这棵树进行一次遍历，给定点 $u$，求 $u$ 在 $p$ 中的位置。

$1\le n,Q\le 10^5$。

Part1 答案咋算

考虑这么一棵树，$u,v$ 分别是 $fa$ 的左儿子和右儿子。考虑 $fa$ 分别进行前序遍历、中序遍历、后序遍历时对于 $u,v$ 的子树的影响。图中中括号的部分即为 $u,v$ 的子树。假设 $fa$ 一开始是中序遍历，那么当 $fa$ 变成前序遍历时，可以发现 $u$ 整颗子树向后挪了一步；当 $fa$ 变成后序遍历的时候，$v$ 整颗子树向前挪了一步。

设 $f(u)$ 表示 $u$ 在 $p$ 中的位置。也就是说，对于 $u$ 的整颗子树 $t{r}_u$，从所有祖先都是中序遍历开始，每有一个祖先 $anc$（包括点 $u$）满足 $anc$ 是其父亲的左儿子，并且采用先序遍历，那么 $\forall v\in t{r}_u$，$f(v)$ 的值都会加一；每有一个祖先 $anc$（包括点 $u$）满足 $anc$ 是其父亲的右儿子，并且采用后序遍历，那么 $\forall v\in t{r}_u$，$f(v)$ 的值都会减一。也就是说，我们需要对于每个点 $u$ 维护出其祖先中分别满足上述两种条件的祖先的数量，这样就可以简单的根据 $u$ 的标记快速得出 $f(u)$。假设我们得出在中序遍历下点 $u$ 的位置是 $f_0(u)$，维护出的 $u$ 的偏移量是 $\Delta$；那么 $u$ 进行中序遍历的答案就是 $f_0(u)+\Delta$，其他两种情况只需要分别减去左子树大小或加上右子树大小即可。

Part2 怎么维护

不妨考虑每个点对其子树的贡献。我们设 $ta{g}_1(u)$ 表示 $u$ 有几个祖先 $anc$ 满足 $anc$ 是其父亲的左儿子，并且采用先序遍历；$ta{g}_2(u)$ 表示 $u$ 有几个祖先 $anc$ 是其父亲的右儿子，并且采用后序遍历。对于点 $u$：

• 如果 $u$ 是其父亲 $f{a}_u$ 的左儿子，且 $x_u=-1$，那么 $u$ 就对 $\forall v\in t{r}_u$（也包括 $u$）的 $ta{g}_1(u)$ 有 $1$ 的贡献；
• 如果 $u$ 是其父亲 $f{a}_u$ 的右儿子，且 $x_u=1$，那么 $u$ 就对 $\forall v\in t{r}_u$（也包括 $u$）的 $ta{g}_2(u)$ 有 $1$ 的贡献。

不妨考虑所有修改的区间长度都为 $1$ 的部分分，那就是对 $ta{g}_1,ta{g}_2$ 中 $u$ 的子树部分进行一个子树加减（删掉旧标记的贡献，加上新标记的贡献），询问就是单点查，用差分树状数组维护 dfn 上的区间和即可。扩展到原问题，我们考虑进行分块。

• 修改：
  • 对于一个整块，也就是说更新块内的所有点标记都相同。不妨维护一个 $cn{t}_l(k,i)$ 表示对于点 $i$，其祖先（和点 $i$）中有多少个点 $anc$ 在块 $k$ 中且是 $anc$ 的父亲的左儿子；同理维护一个 $cn{t}_r(k,i)$ 表示 $i$ 祖先中是右儿子且在块 $k$ 内的祖先的个数。那对点 $i$ 的贡献就很好算了，记 $ta{g}_k$ 表示块 $k$ 的标记都是 $ta{g}_k$，那么当 $ta{g}_k=-1$ 时这个块就对任意点 $u$ 有 $cn{t}_l(k,u)$ 的偏移量贡献；类似当 $ta{g}_k=1$ 时就有 $-cn{t}_r(k,u)$ 的偏移量贡献。
  • 对于一个散块，直接考虑把整个块原来的信息扬了，暴力把每个点最新的标记求出来，然后每个块整两个树状数组表示这个块中的点对整棵树的贡献，按照之前的方法把贡献重新算好即可。
  • 也就是说，当这个块是整块的时候我们看 $cn{t}_l,cn{t}_r$ 和 $tag$ 的信息，否则看两个树状数组的信息。
• 查询：按照上面说的枚举每个块查询即可。可能需要特判一下根节点，反正我判了。

这个东西时间复杂度 $O(n\sqrt{n}\log n)$，luqyou 根据此做法获得了 68pts，前途貌似不是很光明……

Part3 优化！

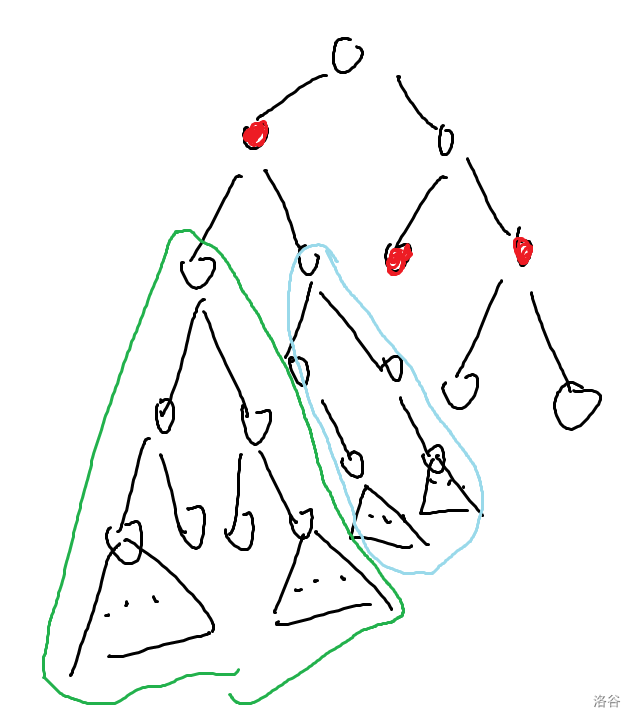
考虑这么一棵树，其中红色的点是当前块内的点。考虑这两个分别用绿色和浅蓝色圈起来的两棵子树，可以发现在两个树状数组中，它们的值是一样的！也就是说，对于块 $k$ 和一个块外点 $u$，我们只需要找到 $u$ 中深度最深的在块里的祖先（如果没有就说明这个块对 $u$ 没有贡献）$anc$，用 $anc$ 维护的答案再简单根据自己在 $anc$ 的左右子树和 $anc$ 此时的标记做一些微调就得到了 $u$ 的答案！再考虑一个块内点的答案，也是按照其块内祖先的答案加上自己的贡献计算的！

我们不妨把块中的点拿到原树上去建出一个虚树，那么树状数组只需维护这个虚树的子树和就可以了；对于块中点直接查树状数组，其他点找到自己在原树的祖先中深度最深的虚树中的点，查这个点的答案并按照上面说的改一改即可。现在时间复杂度优化到了 $O(n\sqrt{n}\log \sqrt{n})$！可是 1000ms 的时限让 under_the_time 感到头疼……

Part4 优化！！

这个复杂度还是有点悬。注意到树状数组的操作实际上是在支持我们动态对块中某个点改标记，但是本来整个块都被扬了，每个点的新标记也都已经确定，为啥一定要在线呢？我们在虚树上先计算出每个点单独对子树的贡献存在这个点上，然后做个祖先和就可以了！这样时间复杂度 $O(n\sqrt{n})$ 足以通过本题……吗？

// 在线做法
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5;
int n, Q, f[maxn], son[maxn][2], fa[maxn], clo, siz[maxn]; short x[maxn];
void init_dfs(int u) {siz[u] = 1;if (son[u][0])fa[son[u][0]] = u, init_dfs(son[u][0]), siz[u] += siz[son[u][0]];f[u] = ++ clo;if (son[u][1])fa[son[u][1]] = u, init_dfs(son[u][1]), siz[u] += siz[son[u][1]];
} const int maxm = 205, maxl = 505;
int getway(int u) { return son[fa[u]][1] == u; }
short get_x(int u);
namespace FastIn {int read() {char c = getchar(); int f = 1;for (; c < '0' || c > '9'; c = getchar())if (c == '-') f = -f;int s = 0;for (; c >= '0' && c <= '9'; c = getchar())s = (s << 1) + (s << 3) + (c ^ 48);return s * f;} short sread() {char c = getchar(); short f = 1;for (; c < '0' || c > '9'; c = getchar())if (c == '-') f = -f;short s = 0;for (; c >= '0' && c <= '9'; c = getchar())s = (s << 1) + (s << 3) + (c ^ 48);return s * f;}
} using namespace FastIn;
struct BLOCK {int L, R;int id[maxn], vir_cnt;int cnt_left[maxn], cnt_right[maxn];int tag1[maxl << 1], tag2[maxl << 1];int vir_son[maxl << 1][2], vir_fa[maxl << 1];int vir_root; pair<int, bool> anc[maxn];int real_id[maxl << 1];int build(int u, int now_anc, int way) {if (u != 1)cnt_left[u] = cnt_left[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 0), cnt_right[u] = cnt_right[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 1);if (L <= u && u <= R) now_anc = u;else anc[u] = mk(now_anc, way);int res = 0, l = 0, r = 0;if (son[u][0]) l = build(son[u][0], now_anc, now_anc == u ? 0 : way);if (son[u][1]) r = build(son[u][1], now_anc, now_anc == u ? 1 : way);if (l && r || L <= u && u <= R)  {res = id[u] = ++ vir_cnt, real_id[res] = u;if (l) vir_fa[l] = res, vir_son[res][0] = l;if (r) vir_fa[r] = res, vir_son[res][1] = r;} else if (l || r) res = (l | r);return res;} short tag;void update(int u) {if (vir_fa[u]) tag1[u] += tag1[vir_fa[u]], tag2[u] += tag2[vir_fa[u]];if (vir_son[u][0]) update(vir_son[u][0]);if (vir_son[u][1]) update(vir_son[u][1]);} void chg_tag(int l, int r, int new_tag) {for (int i = L; i <= R; i ++) {tag1[id[i]] = tag2[id[i]] = 0;if (tag != 2) x[i] = l <= i && i <= r ? new_tag : tag;else if (l <= i && i <= r) x[i] = new_tag;} tag = 2;} int get_virway(int u) {return vir_son[vir_fa[u]][1] == u;}void rebuild() {for (int i = L; i <= R; i ++) {if (id[i] == vir_root || real_id[vir_fa[id[i]]] < L || real_id[vir_fa[id[i]]] > R) continue;if (get_virway(id[i]) == 0 && get_x(real_id[vir_fa[id[i]]]) == -1) tag1[id[i]] = 1;if (get_virway(id[i]) == 1 && get_x(real_id[vir_fa[id[i]]]) == 1) tag2[id[i]] = 1;} update(vir_root);}
} b[maxm]; int bel[maxn];
short get_x(int u) { if (b[bel[u]].tag == 2) return x[u];return b[bel[u]].tag;
}
bool MemoryED; int main() { // open(uoj7);n = read(), Q = read();for (int i = 1; i <= n; i ++)son[i][0] = read(), son[i][1] = read(), x[i] = 0;init_dfs(1); int m = maxl - 5, k = 1;for (int i = 1; i <= n; i += m, k ++) {b[k].L = i, b[k].R = min(n, i + m - 1), b[k].vir_cnt = 0;for (int j = i; j < i + m && j <= n; j ++)bel[j] = k;b[k].vir_root = b[k].build(1, 0, 0), b[k].tag = -1;} k --; for (int _ = 1, op, l, r, u; _ <= Q; _ ++) {op = read();if (op == 1) {l = read(), r = read(); short new_x = sread();if (bel[l] == bel[r]) b[bel[l]].chg_tag(l, r, new_x), b[bel[l]].rebuild();else {b[bel[l]].chg_tag(l, b[bel[l]].R, new_x), b[bel[r]].chg_tag(b[bel[r]].L, r, new_x);for (int i = bel[l] + 1; i < bel[r]; i ++)b[i].tag = new_x;b[bel[l]].rebuild(), b[bel[r]].rebuild();}} else {u = read(); short x_u = get_x(u);if (u == 1) { printf("%d\n", x_u == -1 ? 1 : x_u == 0 ? f[u] : n); continue; }int ans = x_u == -1 ? f[u] - siz[son[u][0]] : x_u == 0 ? f[u] : f[u] + siz[son[u][1]];// cout << "pre ans: " << ans << '\n';for (int i = 1; i <= k; i ++) {// cout << b[i].L << ' ' << b[i].R << ':';if (b[i].tag != 2) {ans += (b[i].tag == -1) * b[i].cnt_left[u] - (b[i].tag == 1) * b[i].cnt_right[u];// cout << (b[i].tag == -1) * b[i].cnt_left[u] << ' ' << (b[i].tag == 1) * b[i].cnt_right[u] << '\n';} else if (b[i].L <= u && u <= b[i].R) {ans += b[i].tag1[b[i].id[u]] - b[i].tag2[b[i].id[u]];// cout << b[i].tag1[u] << ' ' << b[i].tag2[u] << '\n';} else {auto [anc, way] = b[i].anc[u];if (anc == 0) continue;ans += b[i].tag1[b[i].id[anc]] + (way == 0 && get_x(anc) == -1) - (b[i].tag2[b[i].id[anc]] + (way == 1 && get_x(anc) == 1));// cout << b[i].tag1[anc] + (way == 0 && get_x(anc) == -1) << ' ' << (b[i].tag2[anc] + (way == 1 && get_x(anc) == 1)) << '\n';}} printf("%d\n", ans);}} cerr << cost_time << '\n';return 0;
}

Part5 优化！！！

实测发现这么做空间复杂度常数爆炸，即使使用 short 也无力通过最后 5 个点。我们考虑把操作和询问离线下来，然后先枚举块再枚举操作和询问，每次只考虑操作对这个块的影响以及这个块对答案的贡献。其实稍微改改就好了，常数显著优化。

// 离线做法
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0) << "KB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5;
int n, Q, f[maxn], son[maxn][2], fa[maxn], clo, siz[maxn]; short x[maxn];
void init_dfs(int u) {siz[u] = 1;if (son[u][0])fa[son[u][0]] = u, init_dfs(son[u][0]), siz[u] += siz[son[u][0]];f[u] = ++ clo;if (son[u][1])fa[son[u][1]] = u, init_dfs(son[u][1]), siz[u] += siz[son[u][1]];
} const int maxm = 205, maxl = 505;
int getway(int u) { return son[fa[u]][1] == u; }
short get_x(int u);
namespace FastIn {int read() {char c = getchar(); int f = 1;for (; c < '0' || c > '9'; c = getchar())if (c == '-') f = -f;int s = 0;for (; c >= '0' && c <= '9'; c = getchar())s = (s << 1) + (s << 3) + (c ^ 48);return s * f;} short sread() {char c = getchar(); short f = 1;for (; c < '0' || c > '9'; c = getchar())if (c == '-') f = -f;short s = 0;for (; c >= '0' && c <= '9'; c = getchar())s = (s << 1) + (s << 3) + (c ^ 48);return s * f;}
} using namespace FastIn;
struct BLOCK {int L, R;short id[maxn], vir_cnt; int real_id[maxl << 1];short cnt_left[maxn], cnt_right[maxn];short tag1[maxl << 1], tag2[maxl << 1];short vir_son[maxl << 1][2], vir_fa[maxl << 1];short vir_root; pair<int, bool> anc[maxn];short build(int u, int now_anc, bool way) {if (u != 1)cnt_left[u] = cnt_left[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 0), cnt_right[u] = cnt_right[fa[u]] + (L <= fa[u] && fa[u] <= R && getway(u) == 1);if (L <= u && u <= R) now_anc = u;else anc[u] = mk(now_anc, way);short res = 0, l = 0, r = 0;if (son[u][0]) l = build(son[u][0], now_anc, now_anc == u ? 0 : way);if (son[u][1]) r = build(son[u][1], now_anc, now_anc == u ? 1 : way);if (l && r || L <= u && u <= R)  {res = id[u] = ++ vir_cnt, real_id[res] = u;if (l) vir_fa[l] = res, vir_son[res][0] = l;if (r) vir_fa[r] = res, vir_son[res][1] = r;} else if (l || r) res = (l | r);return res;} short tag;void update(short u) {if (vir_fa[u]) tag1[u] += tag1[vir_fa[u]], tag2[u] += tag2[vir_fa[u]];if (vir_son[u][0]) update(vir_son[u][0]);if (vir_son[u][1]) update(vir_son[u][1]);} int get_virway(int u) {return vir_son[vir_fa[u]][1] == u;}void rebuild(int l, int r, short new_tag) {for (int i = L; i <= R; i ++) {tag1[id[i]] = tag2[id[i]] = 0;if (tag != 2) x[i] = l <= i && i <= r ? new_tag : tag;else if (l <= i && i <= r) x[i] = new_tag;} tag = 2;for (int i = L; i <= R; i ++) {if (id[i] == vir_root || real_id[vir_fa[id[i]]] < L || real_id[vir_fa[id[i]]] > R) continue;if (get_virway(id[i]) == 0 && get_x(real_id[vir_fa[id[i]]]) == -1) tag1[id[i]] ++;if (get_virway(id[i]) == 1 && get_x(real_id[vir_fa[id[i]]]) == 1) tag2[id[i]] ++;} update(vir_root);}
} b; 
// 以上基本不变
short get_x(int u) { if (b.tag == 2) return x[u];return b.tag;
} struct Query {int op, l, r, u; short new_x;
} que[maxn]; int ans[maxn];
bool MemoryED; int main() { open(uoj13);// cerr << cost_space << '\n';n = read(), Q = read();for (int i = 1; i <= n; i ++)son[i][0] = read(), son[i][1] = read(), x[i] = 0;for (int i = 1; i <= Q; i ++) {auto &[op, l, r, u, new_x] = que[i];op = read();if (op == 1) l = read(), r = read(), new_x = sread();else u = read();}init_dfs(1); short m = maxl - 5;for (int _ = 1; _ <= n; _ += m) {for (int i = 1; i <= b.vir_cnt; i ++)b.tag1[i] = b.tag2[i] = 0, b.vir_fa[i] = 0, b.vir_son[i][0] = b.vir_son[i][1] = 0;for (int i = 1; i <= n; i ++)b.anc[i] = mk(0, 0), b.id[i] = b.cnt_left[i] = b.cnt_right[i] = x[i] = 0;b.L = _, b.R = min(n, _ + m - 1), b.vir_cnt = b.vir_root = 0;b.vir_root = b.build(1, 0, 0), b.tag = -1;for (int q = 1; q <= Q; q ++) {auto [op, l, r, u, new_x] = que[q];if (op == 1) {if (l <= b.L && b.R <= r) { b.tag = new_x; continue; }if (r < b.L || b.R < l) continue;b.rebuild(l, r, new_x);} else {int &ans = :: ans[q];if (u == 1) {if (b.L <= u && u <= b.R) {short x_u = get_x(u);ans += x_u == -1 ? 1 : x_u == 0 ? f[u] : n;} continue;} if (b.L <= u && u <= b.R) {short x_u = get_x(u);ans += x_u == -1 ? f[u] - siz[son[u][0]] : x_u == 0 ? f[u] : f[u] + siz[son[u][1]];}if (b.tag != 2) {ans += (b.tag == -1) * b.cnt_left[u] - (b.tag == 1) * b.cnt_right[u];} else if (b.L <= u && u <= b.R) {ans += b.tag1[b.id[u]] - b.tag2[b.id[u]];} else {auto [anc, way] = b.anc[u];if (anc == 0) continue;ans += b.tag1[b.id[anc]] + (way == 0 && get_x(anc) == -1) - (b.tag2[b.id[anc]] + (way == 1 && get_x(anc) == 1));// cout << b[i].tag1[anc] + (way == 0 && get_x(anc) == -1) << ' ' << (b[i].tag2[anc] + (way == 1 && get_x(anc) == 1)) << '\n';}}}} for (int i = 1; i <= Q; i ++)if (que[i].op == 2) printf("%d\n", ans[i]);return 0;
}
/*
6 6
2 0
3 0
4 0
5 0
6 0
0 0
2 6
1 2 4 -1
1 1 6 -1
1 2 4 1
1 1 6 -1
2 6
*/

Part6 一些细节

• 存储虚树相关信息的一些数组都可以开成 short，因为虚树点数一共不超过 short 的范围。
• 块外点存块内点最近的祖先时必须保证这个祖先在块内（在虚树上不等于在块上，实际上这个虚树只是用来在重构块信息后用来统计祖先和的），而且还要记录它在这个祖先的哪个子树里。
• 当你重构整个块之后、重新计算 $ta{g}_1,ta{g}_2$ 时，应当按照虚树上的结构判断而不是原树结构，也类似的需要判断这对父子是否也都在块中，否则会出现一个点在多个虚树中被统计多次的问题。（参考代码中 rebuild 的部分）xyd 数据太水了导致我一开始写错都能 AC。
• 精细实现！精细实现！精细实现！