LSTM入门案例(时间序列预测)
需求
假如我有一个时间序列,例如是前113天的价格数据(训练集),然后我希望借此预测后30天的数据(测试集),实际上这143天的价格数据都已经有了。这里为了简单,每一天的数据只有一个价格维度(转化成矩阵形式就是1列),但实际上每一天的数据也可以是多维的特征,转化成矩阵就是多列。
预测思路
首先训练模型去预测下一天数据的能力,训练完后,我们使用历史数据预测第114天的数据,预测后,我们暂时将第114天的数据看做真实数据,放入历史数据中,再用它预测第115天的数据,依次类推,最终预测完后30天的数据。
本实现的关键点
1. 数据预处理:归一化很重要,可以加速训练过程并提高模型性能
2. 模型结构:LSTM + 全连接层的组合用于回归预测
3. 训练过程:使用MSE损失和Adam优化器
4. 预测方式:滚动预测,保持隐藏状态的连续性
一、LSTM神经元结构
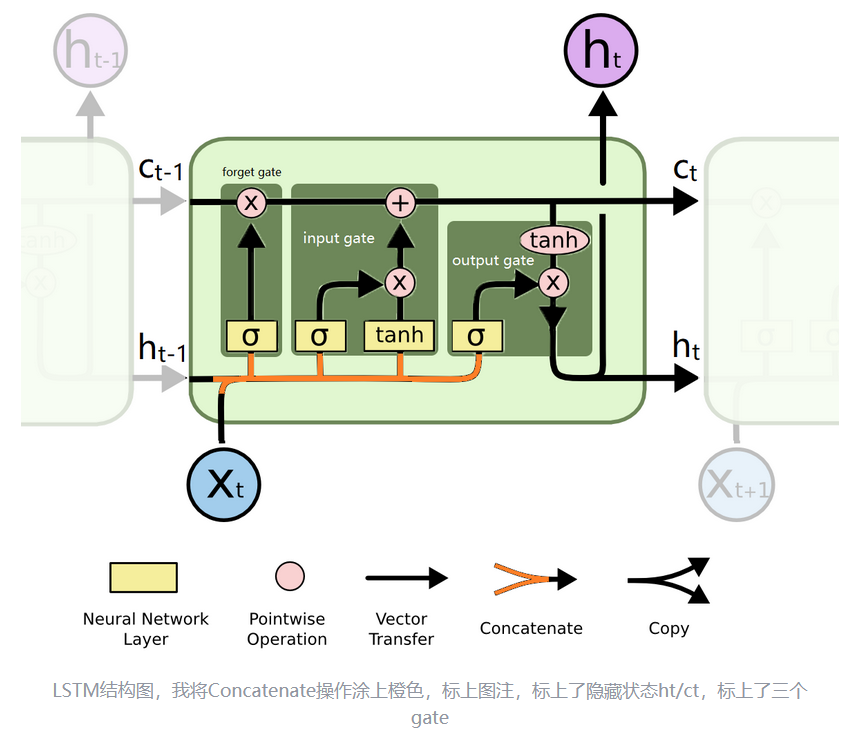


二、定义LSTM模型
下面我们定义LSTM回归模型,它包括:
1. LSTM层:处理时间序列数据并捕捉时间依赖关系
2. 回归层:将LSTM的输出映射到预测值
我们会使用torch.nn.LSTM()加载LSTM层。其参数定义如下:

input(seq_len, batch_size, input_dim)
参数有:
seq_len:序列长度,在NLP中就是句子长度,一般都会用pad_sequence补齐长度
batch_size:每次喂给网络的数据条数,在NLP中就是一次喂给网络多少个句子
input_dim:特征维度,和前面定义网络结构的input_size一致。
output,(ht, ct) = net(input)
output: 最后一个状态的隐藏层的神经元输出
ht:最后一个状态的隐含层的状态值
ct:最后一个状态的隐含层的遗忘门值
请注意,虽然通常情况下张量的第一个维度是批次大小batch size,但是PyTorch建议我们输入循环网络的时候张量的第一个维度是序列长度,而第二个维度才是批次数量。
那么输入此LSTM的 input.size() == (seq_len, batch_size, inp_dim)
在我们的LSTM时间序列预测任务中:
seq_len:时间序列的长度,在这里使用前113天的价格数据进行训练,则 seq_len == 113。
batch_size:同个批次中输入的序列条数。
inp_dim:输入数据的维度,在这里价格一个维度,则 inp_dim == 1。如果是自然语言处理 (NLP) ,那么:
seq_len 将对应句子的长度
batch_size 同个批次中输入的句子数量
inp_dim 句子中用来表示每个单词(中文分词)的矢量维度
接下来根据LSTM的输入,我们可以确定LSTM的参数:
rnn = nn.LSTM(inp_dim, mid_dim, num_layers)
# inp_dim 是LSTM输入张量的维度,我们已经根据我们的数据确定了这个值是1。
# mid_dim 是LSTM三个门 (gate) 的网络宽度,也是LSTM输出张量的维度。
# num_layers 是使用多少个LSTM对数据进行预测,然后将他们的输出堆叠起来。(一般设置两层LSTM,默认参数是1层)
input = torch.randn(seq_len, batch_size, inp_dim)
output = rnn(input)
assert output.size() == (seq_len, batch_size, mid_dim)
为了进行时间序列预测,我们在LSTM后面接上两层全连接层(1层亦可),同时改变最终输出张量的维度,我们只需要预测价格这一个值,因此out_dim 为1。在LSTM后方的全连接层也可以看做是一个回归操作 regression。
在LSTM后面接上两层全连接层,为何是两层: 理论上足够宽,并且至少存在一层具有任何一种“挤压”性质的激活函数的两层全连接层就能拟合任何连续函数。最先提出这个理论证明的是 Barron et al., 1993,使用了UAT (Universal Approximation Theorem),指出了可以在compact domain拟合任意多项式函数。”
实际上对于过于复杂的连续函数,这个「足够宽」不容易满足。并且拟合训练数据并让神经网络具备足够的泛化性的前提是:良好的训练方法(比如批次训练数据满足 独立同分布 (i.i.d.),良好的损失函数,满足Lipschitz连续 etc.)
reg = nn.Sequential(
nn.Linear(mid_dim, mid_dim), # 全连接层,将LSTM输出映射到mid_dim维度
nn.Tanh(), # 激活函数,将输出映射到[-1, 1]之间
nn.Linear(mid_dim, out_dim), # 全连接层,将LSTM输出映射到out_dim维度
) # regression回归input = output_of_LSTM
[seq_len, batch_size, mid_dim]= input.shape
input = input.view(seq_len * batch_size, mid_dim) # 将输出重塑为2D
output = reg(input) # 通过回归层
output = output.view(seq_len, batch_size, out_dim) # 重塑回原始形状
定义LSTM模型的完整代码如下:
class RegLSTM(nn.Module):def __init__(self, inp_dim, out_dim, mid_dim, mid_layers):"""初始化LSTM回归模型参数:inp_dim: 输入维度out_dim: 输出维度mid_dim: LSTM隐藏层维度mid_layers: LSTM层数"""super(RegLSTM, self).__init__()# LSTM层,输入维度为inp_dim,隐藏状态维度为mid_dim,层数为mid_layersself.rnn = nn.LSTM(inp_dim, mid_dim, mid_layers) # 回归层,将LSTM输出映射到预测值self.reg = nn.Sequential(nn.Linear(mid_dim, mid_dim), # 全连接层,将LSTM输出映射到mid_dim维度nn.Tanh(), # 激活函数,将输出映射到[-1, 1]之间nn.Linear(mid_dim, out_dim), # 全连接层,将LSTM输出映射到out_dim维度) def forward(self, x):"""前向传播参数:self.rnnx: 输入数据,形状为 [seq_len, batch_size, inp_dim]返回:输出预测,形状为 [seq_len, batch_size, out_dim]"""# 获取LSTM输出,y形状为 [seq_len, batch_size, mid_dim]y = self.rnn(x)[0] # y, (h, c) = self.rnn(x) # 获取输出的形状seq_len, batch_size, hid_dim = y.shape# 将输出重塑为2D,便于全连接层处理y = y.view(-1, hid_dim) # 通过回归层y = self.reg(y) # 重塑回原始形状y = y.view(seq_len, batch_size, -1) return ydef output_y_hc(self, x, hc):"""带隐藏状态的前向传播,用于预测时保持状态连续性参数:x: 输入数据hc: 上一步的隐藏状态和单元状态元组 (h, c)返回:y: 输出预测hc: 更新后的隐藏状态和单元状态"""# 传递隐藏状态和单元状态y, hc = self.rnn(x, hc)# 与forward相同的处理步骤seq_len, batch_size, hid_dim = y.size() # 获取输出y的形状y = y.view(-1, hid_dim) # 将输出y重塑为2D,便于全连接层处理y = self.reg(y) # 通过回归层y = y.view(seq_len, batch_size, -1) # 重塑回原始形状return y, hc# 示例:LSTM的输入输出维度
print("LSTM输入格式: [seq_len, batch_size, feature_dim]")
print("示例: 5个时间步,3个样本,每个样本10个特征 -> [5, 3, 10]")
forward方法:
LSTM层的输入与输出:out, (ht,Ct)=lstm(input,(h0,C0)),其中
一、输入格式:lstm(input,(h0, C0))
1、input为(seq_len,batch,input_size)格式的tensor,seq_len即为time_step
2、h0为(num_layers * num_directions, batch, hidden_size)格式的tensor,隐藏状态的初始状态
3、C0为(seq_len, batch, input_size)格式的tensor,细胞初始状态
二、输出格式:output,(ht,Ct)
1、output为(seq_len, batch, num_directions*hidden_size)格式的tensor,包含输出特征h_t(源于LSTM每个t的最后一层)
2、ht为(num_layers * num_directions, batch, hidden_size)格式的tensor,
3、Ct为(num_layers * num_directions, batch, hidden_size)格式的tensor,

输入:input,(h_0, c_0)



输出:output,(h_n, c_n)



在LSTM内部,有h和c,可以理解为hidden和cell。模型中定义了两个函数forward()和output_y_hc,可以理解为forward()函数在训练后预测时,会扔掉h和c,每次预测都用同一个h和c(可能是训练时最后一次的h和c,可能是随机的),output_y_hc()会一直返回h和c,从而下一次预测可以把h和c在带进去,一直用最新的h和c。
模型构造函数接受四个参数:inp_dim, out_dim, mid_dim, mid_layers,其中inp_dim, mid_dim, mid_layers是nn.LSTM()构造时传入的3个参数,输入维度是inp_dim,在这里是1,输出维度是mid_dim,这里可以自己定义。后面再跟两个全连接层,第一个全连接层是mid_dim to mid_dim,第二个全连接层是mid_dim to out_dim,也就是说,模型最后的输出维度是out_dim,在本问题中,我们希望预测的是每天的价格,所以out_dim也是1。
REGLSTM这个类里面定义的成员函数output_y_hc,有什么作用?
我们需要保存LSTM的隐藏状态(hidden state),用于恢复序列中断后的计算。举例子,我有完整的序列 seq12345:
- 我输入seq12345 到LSTM后,我能得到6,即seq123456。
- 我也可以先输入 seq123 以及默认的隐藏状态hc,得到4和新的hc。然后我接着把 seq45 以及 hc一起输入到LSTM,我也能得到6,即seq123456。
(hc 指 h和c,是两个张量,本文开头的LSTM结构图注明了何为 h与c)
注意:
- 对于双向 LSTM,正向和反向分别是方向 0 和 1。当输出层拆分时,以
batch_first=False:output.view(seq_len, batch, num_directions, hidden_size)为例。 - 对于双向 LSTM,h_n 与输出的最后一个元素并不等价;前者包含最终的向前和向后隐藏状态,而后者包含最终的向前隐藏状态和初始的向后隐藏状态。
batch_first参数对于非批处理的输入会被忽略。proj_size应该小于hidden_size。
三、数据预处理
3.1 定义数据预处理函数
在模型训练之前,需要对训练集的train_x和train_y都要进行归一化。
train_x, train_x_minmax = minmaxscaler(train_x)
train_y, train_y_minmax = minmaxscaler(train_y)
在模型预测过程,需要对测试集的test_x进行归一化,对predict_y进行反归一化。
test_x = preminmaxscaler(test_x, train_x_minmax[0], train_x_minmax[1])
predict_y = unminmaxscaler(predict_y, train_x_minmax[0], train_y_minmax[1])
划分数据集 --> 对训练集的x和y进行归一化 --> 模型训练 --> 保存模型
循环预测训练集之后的数据:
使用定长的timestep序列数据作为输入来预测下一个数据点--> 对测试集的test_x进行归一化 --> 获取最后一个时间步的预测值test_y[-1].item() --> 对预测值predict_y进行反归一化 --> 将预测结果加入数据集当作真实数据并进行下一步数据点的预测
我们的数据是好几百,我们可以先预处理一下。对x和y,我们进行归一化,之后在模型训练好进行预测的时候,我们还要反归一化将数据还原。对于x和y我们分别归一化。之后在预测的时候,对于输入的x,我们要用训练集x的最大和最小值进行归一化处理,对于预测得到的y,我们要用训练集y的最大和最小值进行反归一化。所以我们要保存着训练集中x和y的最大值与最小值。
直接对全部数据进行归一化处理是不正确的,归一化的时候不应该把测试用的数据也包括进去。
为了提高神经网络的训练效果,我们需要对数据进行归一化处理。下面定义三个函数:
1. `minmaxscaler`: 将数据归一化到[0,1]区间
2. `preminmaxscaler`: 使用已知的最小值最大值对新数据进行归一化
3. `unminmaxscaler`: 将归一化的数据反归一化回原始范围
def minmaxscaler(data):"""将数据归一化到[0,1]区间参数:data: 输入数据返回:scaled_data: 归一化后的数据(min_val, max_val): 用于反归一化的最小值和最大值"""min_val = np.min(data)max_val = np.max(data)scaled_data = (data - min_val) / (max_val - min_val)return scaled_data, (min_val, max_val)def preminmaxscaler(data, min_val, max_val):"""使用已知的最小值和最大值对数据进行归一化参数:data: 输入数据min_val: 最小值max_val: 最大值返回:scaled_data: 归一化后的数据"""scaled_data = (data - min_val) / (max_val - min_val)return scaled_datadef unminmaxscaler(data, min_val, max_val):"""将归一化的数据反归一化参数:data: 归一化的数据min_val: 原始数据的最小值max_val: 原始数据的最大值返回:原始数据"""return data * (max_val - min_val) + min_val# 测试归一化函数
test_data = np.array([1, 5, 10, 15, 20])
normalized_data, (min_val, max_val) = minmaxscaler(test_data)
print("原始数据:", test_data)
print("归一化数据:", normalized_data)
print("反归一化数据:", unminmaxscaler(normalized_data, min_val, max_val))
输出结果:
preminmaxscaler是在预测的时候,我们用训练集的最大最小值去做归一化。
unminmaxscaler就是反归一化。
3.2 准备数据集
- 经过尝试,LSTM对输入的时间序列长度似乎没有要求,也就是说我可以输入100天的历史数据进行训练,我也可以输入50天的历史数据进行训练。之后在训练完进行预测的时候,我也可以输入任意天数的历史数据预测未来的数据。
- 由于数据较少,我们只设置1个batch,也就是一次就把所有训练数据输入进去,然后迭代多个epoch进行训练。
- 我们使用113天的历史数据训练模型,预测后30天的数据。
方法1:只输入一条历史序列进行训练:
最简单的训练模式,我们把113天的历史数据一次性输入到模型中进行训练。113天的历史序列长这样:[112., 118., 132., 129. …… 362., 348., 363.]
那这就是输入模型的x。那么输入模型的y是什么样呢?由于我们希望的是预测后一天的数据,所以我们每次都取后一天的数据,同样构成一个113天的序列,序列长这样:[118., 132., 129., 121. …… 348., 363., 435.]
这就是输入模型的y。可以看到y就是x后移了1天。这里我认为,如果我们想预测后两天你的数据,那么我们的y就可以是x后移2天。
我们构造好了输入数据的x和y,现在要把它们整理成模型希望的数据格式。LSTM希望的输入数据是3维,[seq_len, batch_size, inp_dim]:
seq_len是时间步,也就是每个序列的长度。
batch_size是序列个数,也就是我们希望同时处理多少个序列。
inp_dim是输入数据维度,也就是对于每个时间序列,每一天的数据维数。
对于本问题,我们输入的是一个113天的历史序列,因此batch_size是1。每一天都只有一个价格数据,因此inp_dim也是1。而seq_len就是113。
对于y,y也是一个113天的序列,维度是1,数据格式也是[113, 1, 1]。只不过对应的seq_len具体的值往后移了一位。
# 加载数据 - 时间序列数据(示例可能为区块链或金融数据)
bchain = np.array([112., 118., 132., 129., 121., 135., 148., 148., 136., 119., 104.,118., 115., 126., 141., 135., 125., 149., 170., 170., 158., 133.,114., 140., 145., 150., 178., 163., 172., 178., 199., 199., 184.,162., 146., 166., 171., 180., 193., 181., 183., 218., 230., 242.,209., 191., 172., 194., 196., 196., 236., 235., 229., 243., 264.,272., 237., 211., 180., 201., 204., 188., 235., 227., 234., 264.,302., 293., 259., 229., 203., 229., 242., 233., 267., 269., 270.,315., 364., 347., 312., 274., 237., 278., 284., 277., 317., 313.,318., 374., 413., 405., 355., 306., 271., 306., 315., 301., 356.,348., 355., 422., 465., 467., 404., 347., 305., 336., 340., 318.,362., 348., 363., 435., 491., 505., 404., 359., 310., 337., 360.,342., 406., 396., 420., 472., 548., 559., 463., 407., 362., 405.,417., 391., 419., 461., 472., 535., 622., 606., 508., 461., 390.,432.], dtype=np.float32)# 转为列向量,形状变为(144, 1)
bchain = bchain[:, np.newaxis] # np.newaxis 用于增加列维度,将一维数组转换为二维数组# 查看数据形状
print("数据形状:", bchain.shape)
print("前10个数据点:", bchain[:10].flatten())# 绘制原始数据
plt.figure(figsize=(12, 6))
plt.plot(bchain, 'b-')
plt.title('原始时间序列数据')
plt.xlabel('时间步')
plt.ylabel('值')
plt.grid(True)
plt.show()
输出结果: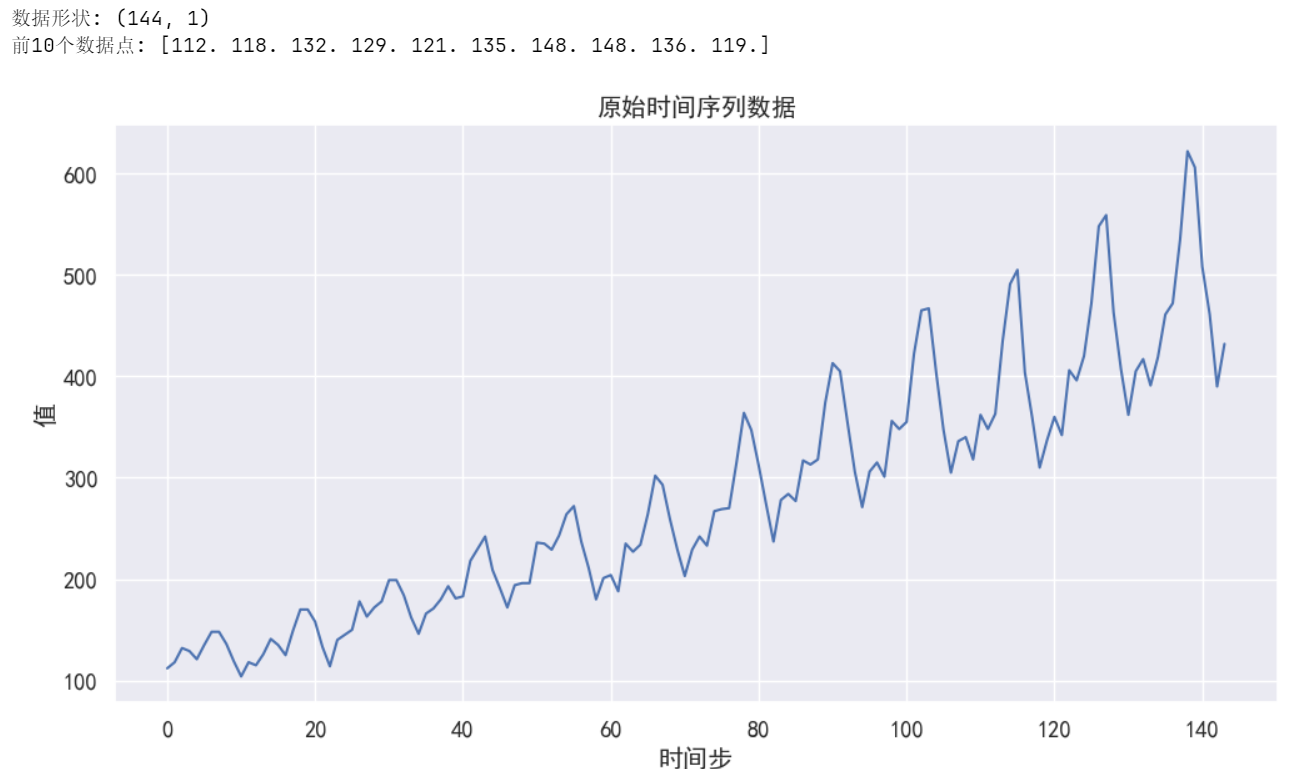
注意:了解np.newaxis的作用、用法
【Numpy】基础学习:一文了解np.newaxis的作用、用法-CSDN博客
【Python】np.newaxis()函数用法详解_np.newaxis函数-CSDN博客
方法2:输入多条短的历史序列进行训练:
我们也可以将使用类似于滑动窗口的方法,从原始数据里选取多段相同长度的序列,作为一条条的历史序列x,当然也要搭配y序列(就是把x序列右移一步)。
我们选定历史序列长度为40,一共选了25个序列,代码如下:
# 第二种操作,用滑动窗口的方法构造数据集
# 将训练数据转换为张量train_x_tensor = torch.tensor(train_x, dtype=torch.float32, device=device)train_y_tensor = torch.tensor(train_y, dtype=torch.float32, device=device)# 使用滑动窗口构造多条序列,窗口长度为40,步长为3window_len = 40batch_x = [] # 存储输入序列batch_y = [] # 存储目标序列for end in range(len(train_x_tensor), window_len, -3):# 添加一段历史序列到batch_xbatch_x.append(train_x_tensor[end-window_len:end])# 添加对应的目标序列到batch_ybatch_y.append(train_y_tensor[end-window_len:end])# 检查构造的序列数量print(f"构造的序列数量: {len(batch_x)}")# 使用pad_sequence将数据整理成LSTM希望的格式# 将多条序列整理成 [seq_len, batch_size, feature_dim] 格式batch_x = pad_sequence(batch_x) # 形状变为 [40, batch_size, 1]batch_y = pad_sequence(batch_y) # 形状变为 [40, batch_size, 1]print(f"batch_x的形状: {batch_x.shape}") # [40, num_sequences, 1]print(f"batch_y的形状: {batch_y.shape}") # [40, num_sequences, 1]
注意:因为pytorch要求timestep必须定长,基本上网上搜到的其他所有pytorch的lstm入门教程都是定长的timestep,如果遇到的案例中使用的是不定长的timestep,需借助pad_sequence成定长的timestep来训练。(但是我整个实验流程都是用的定长的timestep,可忽略这一点)
如果同一批次里面训练序列长度不统一,直接在末尾补0的操作不优雅,我们需要借助torch 自带的工具 pad_sequence的协助,放入pad_sequence 的序列必须从长到短放置,随着反向传播的进行,PyTorch 会逐步忽略完成梯度计算的短序列。具体解释请看PyTorch官网。
「构建用于训练的序列」:要避免输入相同起始裁剪位点的序列用于训练。
我们通过pad_sequence将数据整理成LSTM希望的格式。
比如我们本来有3条历史序列,分别是[1, 2, 3],[4, 5, 6],[7, 8, 9],但是我们将它们整理成的格式为:
原本是: 整理成:
[[1, 2, 3], [[[1], [4], [7]],
[4, 5, 6], [[2], [5], [8]],
[7, 8, 9]] [[3], [6], [9]]]
这样,每一列是一个序列,一共有3个历史序列。每一行是一个时间步,这样整理数据,模型就能一行一行的处理,从而同时处理3个序列。
对于训练用的x和y,我们都整理成一样的格式。只不过在一般的情境中,x的维度要高一点,比如每一天(也就是一个时间步),一共有n个数据表示,也就是说x的维度是n,也就是说在定义LSTM的时候,input_size是n。假如我们有m个序列,每个序列有z个时间步,最后的x要整理成[z, m, n]。
3.3 数据处理与准备
接下来,我们将数据处理成适合LSTM模型训练的格式:
1. 分割数据为输入(X)和目标(Y)
2. 划分训练集和测试集
3. 对数据进行归一化处理
# 设置模型参数
inp_dim = 1 # 输入维度
out_dim = 1 # 输出维度
mid_dim = 8 # LSTM隐藏层维度
mid_layers = 1 # LSTM层数# 准备输入和目标数据
# data_x是从第一个到倒数第二个数据点,data_y是从第二个到最后一个数据点
# 这里我们预测下一个时间步的值
data_x = bchain[:-1, :] # 形状: (143, 1)
data_y = bchain[+1:, :] # 形状: (143, 1)# 查看输入和输出的形状
print("输入数据形状 data_x:", data_x.shape)
print("输出数据形状 data_y:", data_y.shape)# 划分训练集(前113个数据点)
train_size = 113
train_x = data_x[:train_size, :] # 形状: (113, 1)
train_y = data_y[:train_size, :] # 形状: (113, 1)
test_x = data_x[train_size:, :] # 形状: (30, 1)
test_y = data_y[train_size:, :] # 形状: (30, 1)print("训练集 train_x:", train_x.shape)
print("训练集 train_y:", train_y.shape)
print("测试集 test_x:", test_x.shape)
print("测试集 test_y:", test_y.shape)# 数据归一化处理
train_x, train_x_minmax = minmaxscaler(train_x)
train_y, train_y_minmax = minmaxscaler(train_y)# 可视化数据集划分
plt.figure(figsize=(12, 6))
plt.plot(range(len(data_x)), data_x, 'b-', label='原始数据')
plt.axvline(x=train_size, color='r', linestyle='--', label='训练集/测试集分割点')
plt.title('数据集划分')
plt.xlabel('时间步')
plt.ylabel('值')
plt.legend()
plt.grid(True)
plt.show()
输出结果: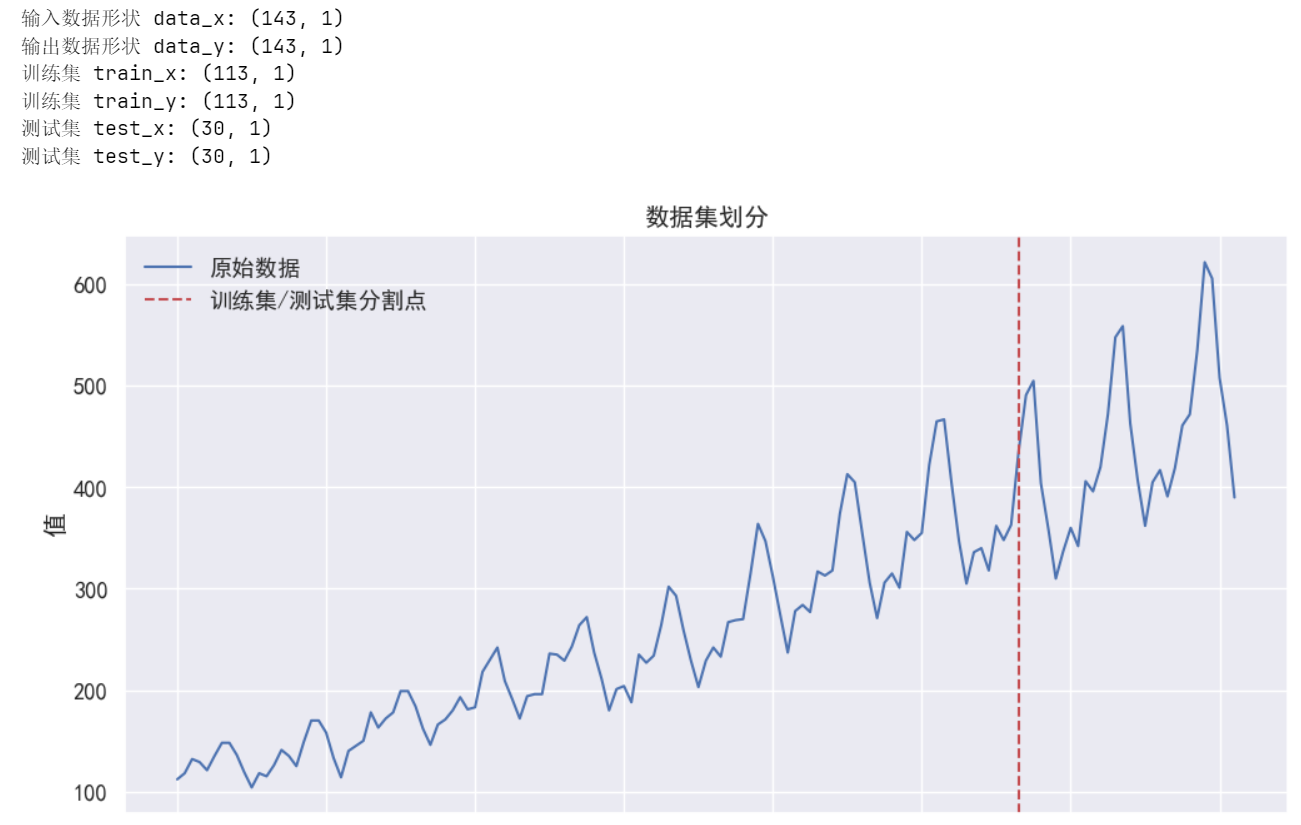
四、模型训练
4.1 准备PyTorch训练数据
有了训练用的x和y,我们就可以将其输入到模型进行训练。代码如下:
将数据转换为PyTorch张量,并设置好LSTM需要的数据格式:
# 设置设备(GPU或CPU)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备: {device}")# 准备训练数据,添加batch维度
# LSTM输入格式: [seq_len, batch_size, feature_dim]
batch_x = train_x[:, np.newaxis, :] # 形状: [113, 1, 1],表示113个时间步,1个样本,每个样本1个特征
batch_y = train_y[:, np.newaxis, :] # 形状: [113, 1, 1]
batch_x = torch.tensor(batch_x, dtype=torch.float32, device=device)
batch_y = torch.tensor(batch_y, dtype=torch.float32, device=device)print("训练输入 batch_x 形状:", batch_x.shape)
print("训练目标 batch_y 形状:", batch_y.shape)输出结果:

4.2 初始化模型、损失函数和优化器
# 初始化模型
model = RegLSTM(inp_dim, out_dim, mid_dim, mid_layers).to(device)
print(model)# 设置损失函数和优化器
loss_fn = nn.MSELoss() # 均方误差损失函数
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2) # Adam优化器
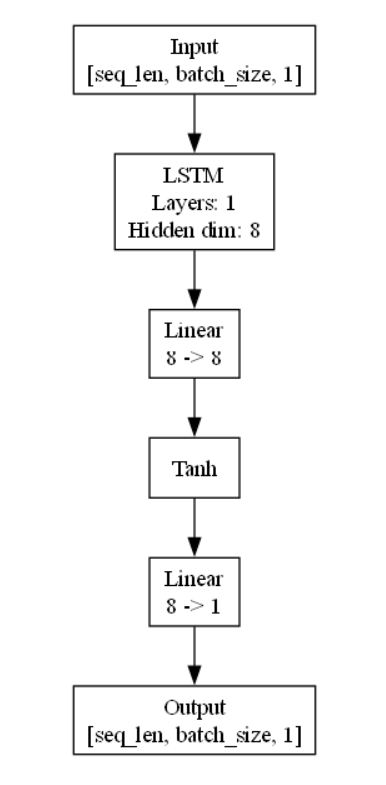
模型结构图如下所示:
4.3 训练模型
我们将训练800个epoch,每10个epoch打印一次损失值:
# 训练模型
print("训练开始...")
losses = [] # 记录损失值,用于绘图epochs = 801
for e in range(epochs):# 前向传播out = model(batch_x) # 将输入数据batch_x传递给模型,得到预测输出out# 计算损失loss = loss_fn(out, batch_y) # 计算预测输出out与真实输出batch_y之间的损失losses.append(loss.item()) # 将损失值添加到losses列表中# 反向传播和优化optimizer.zero_grad() # 清空梯度loss.backward() # 计算梯度optimizer.step() # 更新参数# 每10个epoch打印一次损失if e % 10 == 0:print('Epoch: {:4}, Loss: {:.5f}'.format(e, loss.item()))# 保存模型
torch.save(model.state_dict(), './net.pth')
print("模型已保存至: './net.pth'")# 绘制损失曲线
plt.figure(figsize=(10, 5))
plt.plot(losses)
plt.title('训练损失曲线')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.yscale('log') # 使用对数尺度更容易观察损失下降
plt.grid(True)
plt.show()
数据结果: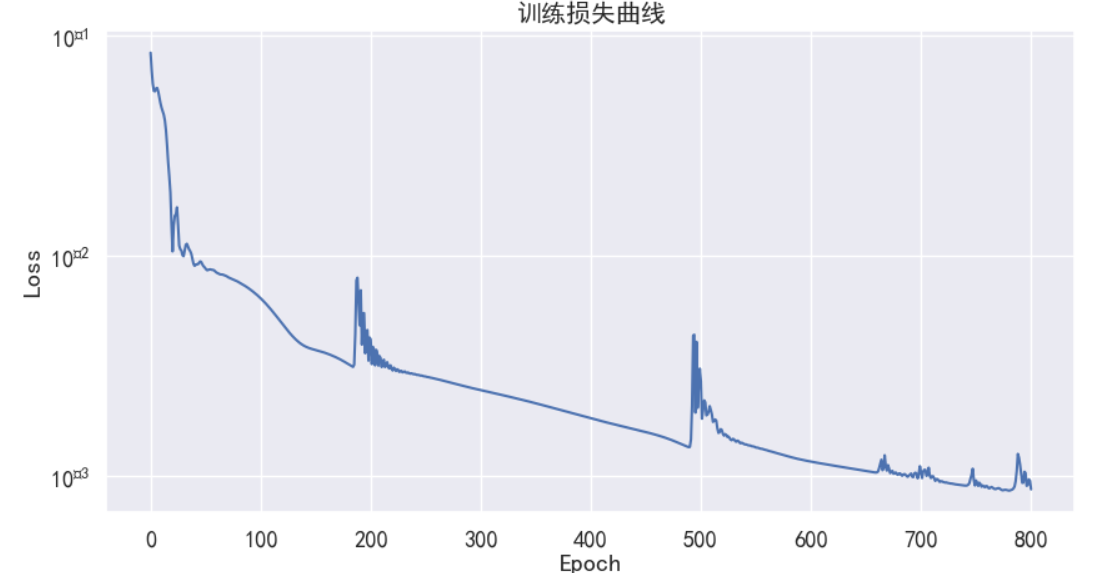
4.4 使用模型进行预测
预测的时候,我们还是要输入一个序列x,得到一个输出序列y。由于在训练时输出序列是输入序列右移一步,因此对于得到的y,其最后一个值就是我们预测的下一天的数据。
对于输入的序列x,序列长度任意,我在尝试的时候发现序列长度长一点和短一点(甚至序列长度是1),预测的效果好像没有差别,这可能证明LSTM的预测效果并不好。我也不太清楚。
现在使用训练好的模型对测试集进行预测:
# 模型预测
print("开始预测...")
new_data_x = data_x.copy()
new_data_x[train_size:] = 0 # 清除训练集之后的数据,用于存放预测结果test_len = 40 # 使用前40个数据点来预测下一个eval_size = 1 # 评估批量大小
# 初始化LSTM隐藏状态和单元状态为零
zero_ten = torch.zeros((mid_layers, eval_size, mid_dim), dtype=torch.float32, device=device)# 循环预测训练集之后的数据
for i in range(train_size, len(new_data_x)):# 获取前test_len个数据点作为输入test_x = new_data_x[i-test_len:i, np.newaxis, :]# 归一化test_x = preminmaxscaler(test_x, train_x_minmax[0], train_x_minmax[1])batch_test_x = torch.tensor(test_x, dtype=torch.float32, device=device)# 如果是第一个预测点,使用初始隐藏状态# 否则,使用上一次预测的隐藏状态继续预测if i == train_size:test_y, hc = model.output_y_hc(batch_test_x, (zero_ten, zero_ten))else:# 仅使用最近的两个时间步来更新状态test_y, hc = model.output_y_hc(batch_test_x[-2:], hc)# 获取完整的预测结果test_y = model(batch_test_x)# 获取最后一个时间步的预测值predict_y = test_y[-1].item()# 反归一化predict_y = unminmaxscaler(predict_y, train_x_minmax[0], train_y_minmax[1])# 保存预测结果new_data_x[i] = predict_yprint(f"预测时间步 {i}, 预测值: {predict_y:.2f}, 真实值: {data_x[i, 0]:.2f}")# 计算测试集的均方误差
test_predictions = new_data_x[train_size:]
test_actual = data_x[train_size:]
mse = np.mean((test_predictions - test_actual) ** 2)
print(f"测试集均方误差 (MSE): {mse:.2f}")
- new_data_x中,前113天是历史数据,后30天是我们要预测的,因此其值都设置为0。
- 我们每次输入40天的数据,并希望预测得到下一天,这样依次将114天、115天直到最后一天的数据预测出来。
- test_x是我们每次输入的40天的历史序列,将其整理成[40, 1, 1]的格式,并进行归一化,然后输入模型。
- 得到的test_y也是一个40天的序列,最后一个值就是我们预测的下一天的值。使用反归一化将其还原,就是预测的下一天的值。我们将其添加到new_data_x的相应位置中。
- hc就是模型的隐状态,这样不断返回模型隐状态,再输入到模型中,应该是效果会比较好。这个我不太清楚。
4.5 可视化预测结果
# 可视化结果
plt.figure(figsize=(12, 6))
plt.plot(new_data_x, 'r', label='预测值')
plt.plot(data_x, 'b', label='真实值', alpha=0.3)
plt.axvline(x=train_size, color='g', linestyle='--', label='训练/测试分界线')
plt.legend(loc='best')
plt.title('LSTM时间序列预测结果')
plt.xlabel('时间步')
plt.ylabel('值')
plt.grid(True)
plt.savefig('prediction_result.png')
plt.show()
print("预测结果已保存至: 'prediction_result.png'")# 放大查看测试集部分
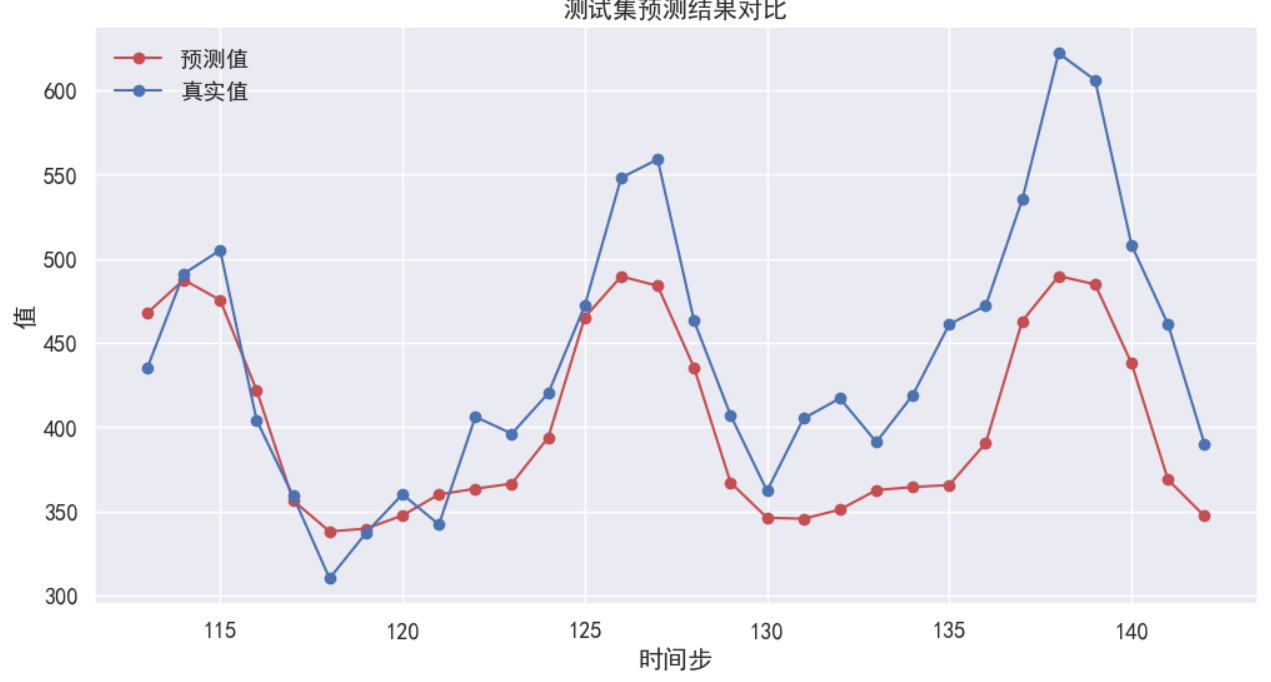
plt.figure(figsize=(12, 6))
plt.plot(range(train_size, len(data_x)), new_data_x[train_size:], 'r-o', label='预测值')
plt.plot(range(train_size, len(data_x)), data_x[train_size:], 'b-o', label='真实值')
plt.title('测试集预测结果对比')
plt.xlabel('时间步')
plt.ylabel('值')
plt.legend(loc='best')
plt.grid(True)
plt.show()
数据结果: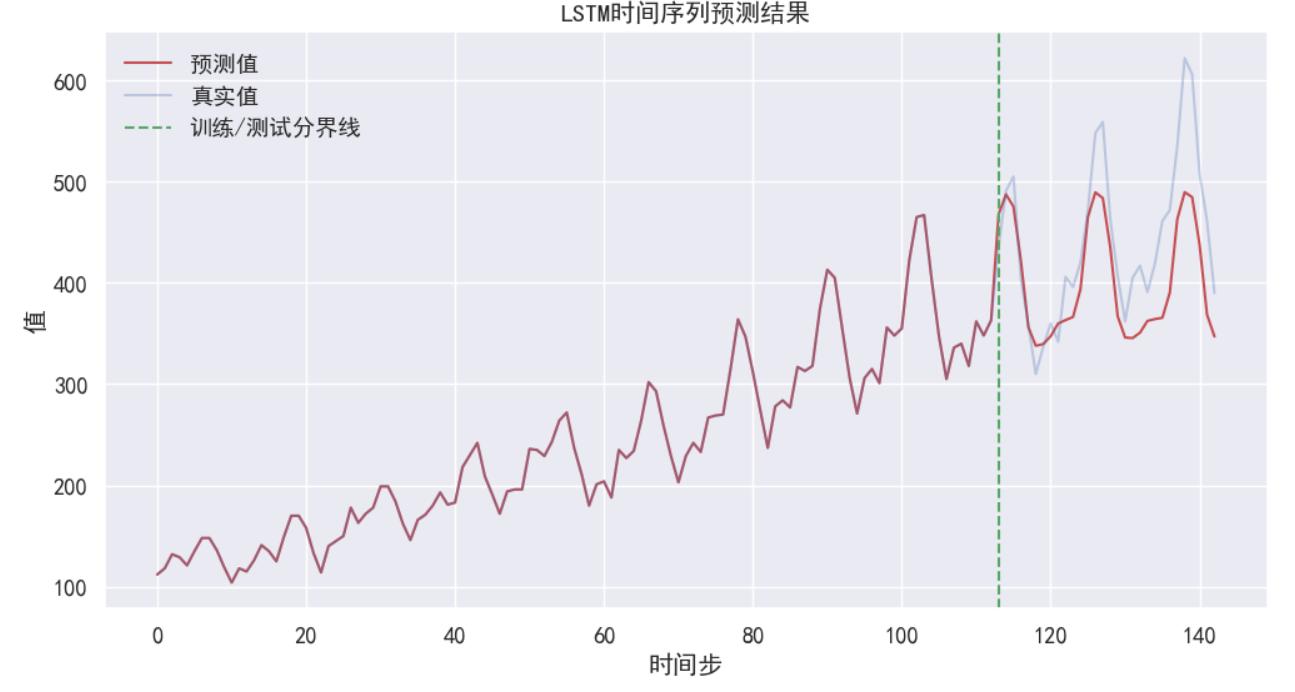
进一步改进方向
1. 调整网络结构(层数、隐藏单元数)
2. 尝试不同的窗口大小
3. 添加更多特征
4. 使用更复杂的损失函数
5. 应用正则化技术防止过拟合
参考文章:
使用LSTM进行简单时间序列预测(入门全流程,包括如何整理输入数据)_lstm 时间序列-CSDN博客
https://zhuanlan.zhihu.com/p/94757947