贝塞尔曲线的切矢量

贝塞尔曲线的切矢量（切线向量）表示曲线在某一点处的方向导数，即曲线在该点的瞬时变化方向。切矢量的计算依赖于贝塞尔曲线的参数方程及其导数。

贝塞尔曲线的定义

一个 n 阶贝塞尔曲线的参数方程为：
$$\mathbf{B}(t)=\sum _{i=0}^n{\mathbf{P}}_i\cdot B_{i,n}(t),t\in [0,1]$$
其中：

• ${\mathbf{P}}_i$ 是控制点，
• $B_{i,n}(t)=\left(\genfrac{}{}{0ex}{}{n}{i}\right)t^i(1-t{)}^{n-i}$ 是伯恩斯坦基多项式。

切矢量的计算

切矢量是贝塞尔曲线的一阶导数 ${\mathbf{B}}^{\prime }(t)$，其表达式为：
$${\mathbf{B}}^{\prime }(t)=\frac{d}{dt}\mathbf{B}(t)=\sum _{i=0}^n{\mathbf{P}}_i\cdot B_{i,n}^{\prime }(t)$$
其中，伯恩斯坦基多项式的导数为：
$$B_{i,n}^{\prime }(t)=n\left[B_{i-1,n-1}(t)-B_{i,n-1}(t)\right]$$
因此，贝塞尔曲线的切矢量可表示为：
$${\mathbf{B}}^{\prime }(t)=n\sum _{i=0}^{n-1}({\mathbf{P}}_{i+1}-{\mathbf{P}}_i)B_{i,n-1}(t)$$

特殊情况

1. 起点 $t=0$ 的切矢量：
   $${\mathbf{B}}^{\prime }(0)=n({\mathbf{P}}_1-{\mathbf{P}}_0)$$
   即切矢量方向为 ${\mathbf{P}}_1-{\mathbf{P}}_0$

2. 终点 $(t=1$) 的切矢量：
   $${\mathbf{B}}^{\prime }(1)=n({\mathbf{P}}_n-{\mathbf{P}}_{n-1})$$
   方向为 ${\mathbf{P}}_n-{\mathbf{P}}_{n-1}$。

几何意义

• 切矢量 ${\mathbf{B}}^{\prime }(t)$ 表示曲线在参数 (t$ 处的运动方向。
• 如果${\mathbf{B}}^{\prime }(t)=0$（零矢量），则该点可能是尖点或曲线在该点停滞（需进一步分析高阶导数）。

示例（二次贝塞尔曲线）

对于二阶贝塞尔曲线：
$$\mathbf{B}(t)=(1-t{)}^2{\mathbf{P}}_0+2t(1-t){\mathbf{P}}_1+t^2{\mathbf{P}}_2$$
其切矢量为：
$${\mathbf{B}}^{\prime }(t)=2(1-t)({\mathbf{P}}_1-{\mathbf{P}}_0)+2t({\mathbf{P}}_2-{\mathbf{P}}_1)$$
在 $t=0$ 和$t=1$ 处：
$${\mathbf{B}}^{\prime }(0)=2({\mathbf{P}}_1-{\mathbf{P}}_0),{\mathbf{B}}^{\prime }(1)=2({\mathbf{P}}_2-{\mathbf{P}}_1)$$

Matlab实现

% 定义控制点（示例：3 阶贝塞尔曲线）
P = [0, 0; 1, 2; 3, 1; 4, 3]; % 4 个控制点 → 3 阶贝塞尔曲线% 参数 t 的采样点
t = linspace(0, 1, 100)';% 计算贝塞尔曲线和切矢量
[B, dB] = bezier_curve(P, t);% 绘制初始图形
figure;
hold on;
plot(P(:,1), P(:,2), 'ro-'); % 控制点及控制多边形
% h_curve = plot(B(:,1), B(:,2), 'b-', 'LineWidth', 2); % 贝塞尔曲线
h_tangent = quiver(B(1,1), B(1,2), dB(1,1)/10, dB(1,2)/10, 'r', 'LineWidth', 2, 'MaxHeadSize', 1); % 初始切矢量
title('贝塞尔曲线及其切矢量动画');
xlabel('x');
ylabel('y');
grid on;
axis equal;% 动画显示切矢量
for k = 1:length(t)% 更新切矢量位置set(h_tangent, 'XData', B(k,1), 'YData', B(k,2), 'UData', dB(k,1)/10, 'VData', dB(k,2)/10);% 可选：绘制切矢量的轨迹plot(B(k,1), B(k,2), 'bo', 'MarkerSize', 5);pause(0.05); % 控制动画速度drawnow;
endfunction [B, dB] = bezier_curve(P, t)% P: 控制点矩阵，大小为 (n+1) x 2（二维情况）% t: 参数 t ∈ [0,1]% B: 曲线上的点% dB: 切矢量n = size(P, 1) - 1; % 阶数 = 控制点数 - 1B = zeros(length(t), 2);dB = zeros(length(t), 2);for k = 1:length(t)tk = t(k);% 计算贝塞尔曲线上的点 B(t)B(k, :) = [0, 0];for i = 0:nB(k, :) = B(k, :) + P(i+1, :) * nchoosek(n, i) * tk^i * (1-tk)^(n-i);end% 计算切矢量 dB(t)if n >= 1dB(k, :) = [0, 0];for i = 0:n-1dB(k, :) = dB(k, :) + n * (P(i+2, :) - P(i+1, :)) * nchoosek(n-1, i) * tk^i * (1-tk)^(n-1-i);endendend
end

运行结果：

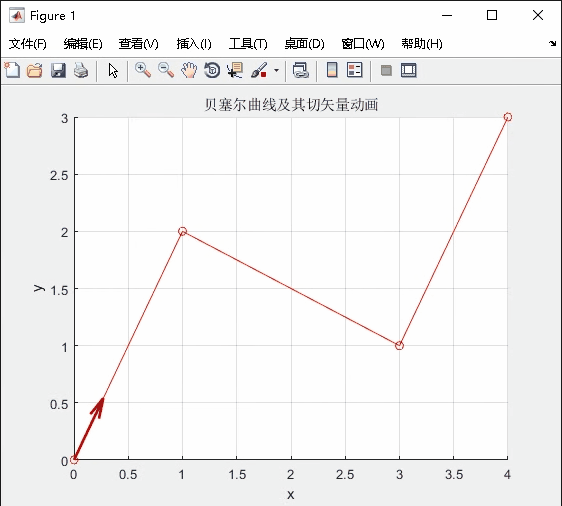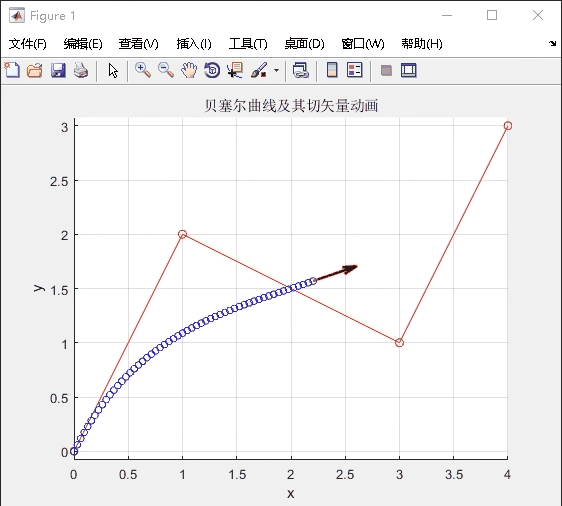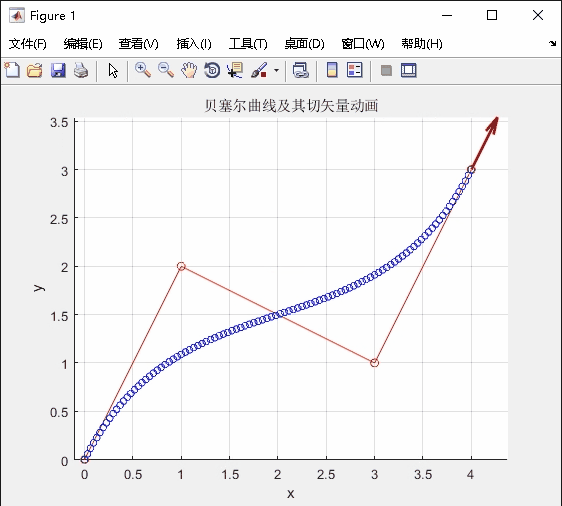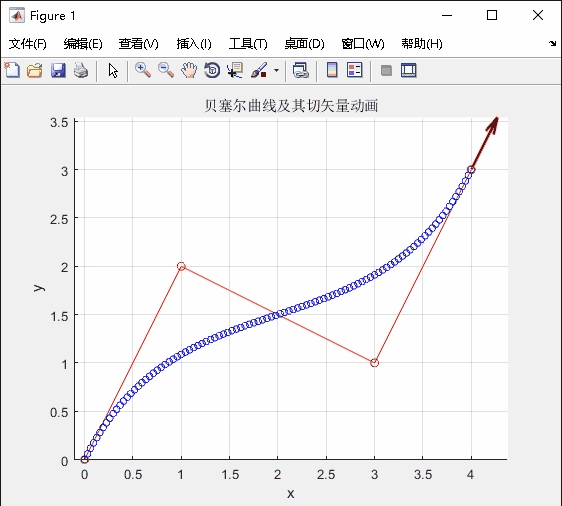
应用

• 曲线平滑性：若相邻贝塞尔曲线段在连接点的切矢量共线，则曲线在该点光滑（G1 连续）。
• 运动控制：在动画或路径规划中，切矢量可用于确定物体的运动方向。

通过计算切矢量，可以分析贝塞尔曲线的局部几何性质，并用于优化设计、插值和碰撞检测等场景。