5.5.1_哈夫曼树

知识总览：

重点是哈夫曼树的构造和哈夫曼树的编码

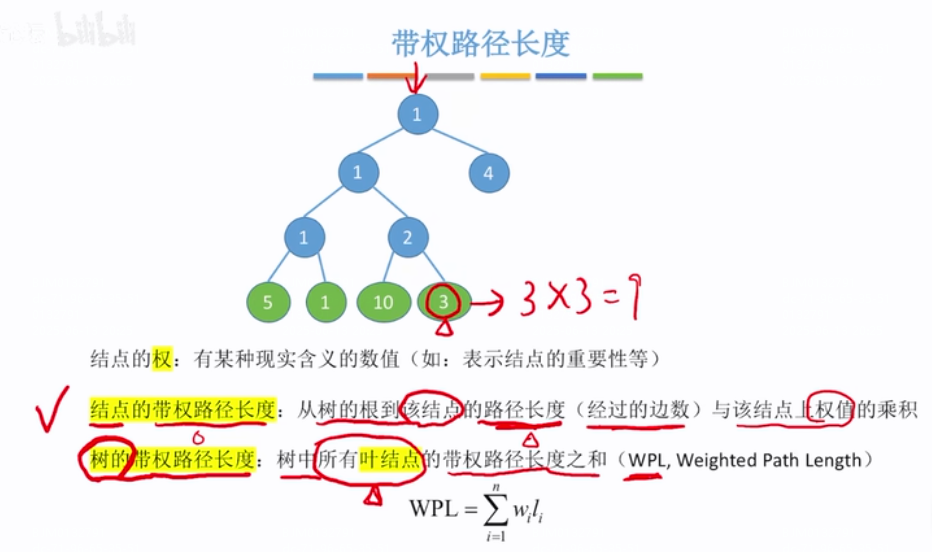
带权路径长度：

节点的权：给树里边的节点赋上一个叫权的东西，然后给权赋予现实意义。如给某个节点赋的权值大小就是表示节点在树里边的重要性

节点的带权路径长度：从根节点到该节点经过了几条边x该节点上的权值=节点的带权路径长度。如下最下边的权值为3的节点，从根节点(权值为1的节点)到该节点有3条边，且该节点权值为3，则该节点带权路径长度=3*3=9

树的带权路径长度(WPL)：为该树的所有的叶节点的带权路径长度之和

哈夫曼树：

哈夫曼树定义：把含有n个带权叶节点的多个二叉树中的树的带权路径长度(wpl)最小的二叉树成为哈夫曼树，也叫最优二叉树【多个相同带权叶节点的二叉树可以构造多种形态的，如下就是4个相同权值的叶节点的不同形态的二叉树，每种形态的二叉树的带权路径长度WPL可能不同，把WPL最小的叫哈夫曼树，如下最小带权路径长度的值为25的即中间的2个二叉树就是哈夫曼树】

如下树的带权路径长度WPL：

只看叶节点，第一个截图的第一个二叉树，叶节点的权值为1，从根节点到权值为1的叶节点有2条边，即该叶节点的带权路径长度=2*1=2，叶节点的权值为3，从根节点到权值为3的叶节点有2条边，即该叶节点的带权路径长度=2*3=6，叶节点的权值为4，从根节点到权值为4的叶节点有2条边，即该叶节点的带权路径长度=2*4=8，叶节点的权值为5，从根节点到权值为5的叶节点有2条边，即该叶节点的带权路径长度=2*5=10，则树带权路径长度为叶节点的带权路径长度之和=2+6+8+10=26

第一个截图的第2个二叉树，叶节点的权值为1，从根节点到权值为1的叶节点有3条边，即该叶节点的带权路径长度=3*1=3，叶节点的权值为3，从根节点到权值为3的叶节点有3条边，即该叶节点的带权路径长度=3*3=9，叶节点的权值为4，从根节点到权值为4的叶节点有2条边，即该叶节点的带权路径长度=2*4=8，叶节点的权值为5，从根节点到权值为5的叶节点有1条边，即该叶节点的带权路径长度=1*5=5，则树带权路径长度为叶节点的带权路径长度之和=3+9+8+5=25

剩下的同

给定权值节点构造哈夫曼树：

 如下给定权值为12237的叶子节点构造哈夫曼树：

第一轮：找2个权值最小的叶子节点补充一个根节点构造一棵树，新树根节点权值=这俩叶子节点的权值之和，如当前权值最小的为1的a和2的c、2的e，可选1的a和2的c(也可选2的2)+一个根节点构造一棵树，新树根节点权值=1+2=3,再选剩余节点(剩余节点包括当前新树根节点)权值最小的2个节点+补充一个根节点构造一棵树

第2轮：新树根节点权值=3，3的b权值也是3，另外一个剩余权值最小的是2的e，选新树根节点(也可选3的b)+2的e+补充一个根节点构造一棵树，新树根节点权值=上一个根节点权值+叶节点权值=3+2=5，再选剩余节点(剩余节点包括当前新树根节点)权值最小的2个节点+补充一个根节点构造一棵树【也可选e和b先结合成一棵树，则这棵树根节点权值= 2+3=5,都可以】

第3轮：新树根节点权值=5，剩余权值最小的是3的b，即这俩+补充一个根节点构造一棵树，新树根节点权值=上一个根节点权值+叶节点权值=5+3=8，再选剩余节点(剩余节点包括当前新树根节点)权值最小的2个节点+补充一个根节点构造一棵树

第3轮：新树根节点权值=8，剩余权值最小的是d的7(就剩这个叶节点了)，即这俩+补充一个根节点再构造一棵树，新树根节点权值=上一个根节点权值+叶节点权值=8+7=15，再选剩余节点(剩余节点包括当前新树根节点)权值最小的2个节点+补充一个根节点构造一棵树

第4轮：无剩余叶节点结束

构造的哈夫曼树的带权路径长度=叶节点的带权路径长度之和，即根节点(权值15)->d节点边数1，权值7，根节点(权值15)->b节点边数2，权值3，根节点(权值15)->e节点边数3，权值2,根节点(权值15)->a节点边数4，权值1，根节点(权值15)->c节点边数4，权值2，即wpl=1*7+2*3+3*2+4*1+4*2=31

结论：

1.开始给出的节点都会变成哈夫曼树叶节点，权值越小的离根节点越远，边数越多，即路径长度越大

2.哈夫曼树节点总数为2n-1【一共有n个节点，每一次两两结结合合并成一棵树，需要合并n-1次，每次合并都会补充增加一个根节点，即一共补充了n-1个根节点，开始给的权值的节点都在哈夫曼树的叶子节点上，其他补充的节点都为非终端节点，所以一共有n+n-1=2n-1个节点】

3.哈夫曼树不存在度为1的节点（目测只有度为0或度为2的节点）

4.哈夫曼树形态并不相同，但是只要是哈夫曼树，带权路径长度一定最小且相等，也是最优的

另外一种形态的哈夫曼树构造(看图2)：

首先选权值最小的2个节点即1的a和2的c(或2的e)，补充一个根节点变成一棵树，树的根节点权值=1+2=3,可以再选剩余节点权值最小的(注意剩余节点权值最小的包括刚刚构造的树的根节点3)，即2的2是最小的，2的e可以和刚构造的树的根节点再加一个根节点构造成一棵树，也可选和3的b构造成一棵树，现在选2的e和3的b+补充一个根节点构造一个树，这个树的根节点权值=2+3=5，此时剩余节点权值为3的根节点、权值为5的根节点、7的d，则权值最小的2个节点是3和5,3和5再加1个根节点构造成一棵树，此时新树根节点权值=3+5=8,8和剩余7的d再加一个根节点构造成一棵树，即新树根节点权值=8+7=15，哈夫曼树WPL=1*7+3*1+3*2+3*2+3*3=31，即即使哈夫曼树形态和上一个并不相同，但是WPL值还是相同的【注意，求哈夫曼树的WPL只求叶子节点的权值，即开始给出的权值的节点的带权路径长度，不求后来每合并一个节点就补充一个节点的带权路径长度】

哈夫曼编码：

定义：用构造哈夫曼树的方法来确定字符集的一种编码方案，字符集中的每个字符都要是哈夫曼树的叶子节点，各个字符出现的频度作为节点的权值，可以把哈夫曼树的左指针看作二进制的0，右指针看作二进制的1(也可以把右指针看成0，左指针看成1，都可以)，因为给定节点构造哈夫曼树的形态不唯一，所以哈夫曼编码也不唯一，但是WPL相等，可以用于数据的压缩

电视上发电报的利用的是哈夫曼编码 0/1

固定长度编码：每个字符用相等长度的二进制位表示，如下：

小渣和老渣敲桌子传答案，不同声响代表ABCD不同答案(让我想起了泰国的一个电影天才枪手)，如果每种情况都用0和1组成的8个固定字符表示太长，即小渣要敲不同声响的桌子8次才能传递一个答案太低效，因为只涉及到4种情况，0和1用两位字符长度就可全部表示出来，故用2个字符表示每种答案，则如下所示表示情况，100道题的不同答案的用01表示的二进制长度之和=80*2+10*2+8*2+2*2=200bit，这种情况类似于树的带权路径长度，把80、10、20、8、2这些答案的个数看成树叶节点权值，把每个答案的二进制长度的表示看成是从根节点到这些叶节点的边的个数，WPL树的带权路径长度即为这100道题答案的二进制字符长度。80题选C，80即为树的叶节点权值，10题选A，10位另外一个叶节点权值，其他同，从根节点向左走表示0，向右走表示1（也可从右走表示0，从左走表示1，都无所谓），即B答案01表示是从根节点先向左走再向右走到达B即01即为从根节点到叶节点B的边数，C答案10，即从根节点先往右走再往左走到达C即10即边长为2，带权路径长度求法和100道题的不同答案的用01表示的二进制长度之和相同。

从固定长度编码--->可变长度编码，可变长度编码：允许对不同字符用不等长的二进制位表示，如下：

如果要让传递答案的二进制长度尽可能的小，即给定了几个节点的权值，每个节点的表示即为根节点到每个节点的边长，则即为求构造哈夫曼树。目前权值有80、10、8、2，先让权值最小的2个节点+补充1个根节点构造一棵树即选8和2，新树根节点权值=8+2=10，剩余节点为新树根节点10、80、10，则让新树根节点10和10+1个根节点构造一棵树，即新树根节点权值=10+10=20，再让新树根节点和80+1个根节点构造一棵树，即新树根节点权值=80+20=100，则如下所示wpl=80*1+10*2+2*3+8*3=130bit，即比上边200bit位又减少了70bit，即如下构造的哈夫曼树中，根节点到C节点路径中有1条边，即C答案用1个二进制位0表示，根节点到C节点路径中有1条边且边上表示0，即C答案用1个二进制位0表示，根节点到A节点路径中分别经过了1和0边，即A答案用2个二进制位10表示，根节点到D节点路径经过了1、1、0边，即D答案用3个二进制位110表示，根节点到B节点路径经过了1、1、1边，即B答案用3个二进制位111表示，即每个字符的二进制位表示不是等长的，即为可变长度编码

总结：把某些现实问题转成求哈夫曼树的带权路径长度表示，即把一些现实问题转成哈夫曼树的带权路径长度定义

假如把可变长度编码中的A答案用1个二进制位1表示，是否能成功：

如果把A答案用1个二进制位1表示，则哈弗曼树改变如下图所示(倒数第3、4张图)，权值10对应的A节点由原来的叶子节点变成C节点的兄弟节点，则此时假如小渣给老渣传答案：CAAABD会传0 111 111 110，则拆解答案可能为0/111/111/110，0-》C，111即可拆解为AAA也可拆解为B，111-》即可拆解为AAA也可拆解为B，110-》D，即答案拆解可能为CBBD答案错误，即因为A答案用编码1表示，和B答案的111以及D答案的110编码都有重合，导致答案有歧义，增加了读编码的难度和准确性，这样的编码为非前缀编码

未改变A答案前即A用10表示：CAAABD会传，0 10 10 10 111 110,完全很清晰，没有一个编码和其他任何编码重叠的可能，如0只能是C答案，10也只能是A答案，也不能看成是101因为没有这样的编码，剩下就是111110，很明显拆成111即B答案，110拆成D答案，因为这也才能和已经定义好的编码对应上

对于一个字符集要设计可变长度编码，所有的字符集中的字符对应到编码树里边都必须是叶子节点，不能是分支节点

前缀编码：没有一个字符的编码是另外一个字符编码的前缀，即不会产生歧义，称为前缀编码

 

知识回顾： 

 

。。。。。。。。。。。