卷积神经网络的参数量及尺度变化计算

前言

本篇博客主要介绍卷积基本概念，卷积神经网络的参数量计算、参数量优化的一些方法（VGG思想，1×1卷积核的应用）、输出图像尺寸的计算，同时也介绍了转置卷积（反卷积）中该如何计算输出图像的尺寸大小。

1.卷积

在深度学习的世界里，卷积操作如同一位默默耕耘的幕后英雄，支撑起图像识别、自然语言处理等众多领域的技术突破。无论是识别交通标志的自动驾驶系统，还是能理解人类语言的智能助手，背后都离不开卷积操作的强大力量。那么，卷积操作究竟是什么？
从数学角度来看，卷积是一种数学运算，用于描述两个函数如何通过某种方式相互作用，产生一个新的函数。在离散的数字信号处理场景下，卷积可以简单理解为两个序列通过特定的乘法和累加运算，得到一个新的序列，具体计算方式可以总结为8个字：翻褶、移位、相乘、相加，具体可见我之前博客的介绍卷积演示系统
而在计算机视觉领域，卷积与之类似，不同的是，处理的数据维度略有不同。
以3×3卷积核为例，其计算公式可以表示为;
$$g(x,y)=\sum _{i=-1}^1\sum _{j=-1}^{1}f(x-i)(x-j)\ast w(i,j)$$
其中w(i,j)表示卷积核，f(x,y)输入图像，g(x,y)为输出图像。
由于在训练过程中，学习的参数是w(i,j)，因此加不加入翻褶区别并不大，因此在视觉领域一般不对卷积和进行翻褶操作。计算公式为：
$$g(x,y)=\sum _{i=-1}^1\sum _{j=-1}^{1}f(x+i)(x+j)\ast w(i,j)$$
这一操作准确来说应该称之为相关操作，但视觉领域一般并不区分这两种操作，统一称之为卷积操作。

2.参数量的计算

在计算机视觉领域，卷积核不仅具有宽和高，还具有深度，常写成宽度×高度×深度的形式。
卷积核的参数不仅包括核中存储的权值，还包括一个偏置值。

2.1案例一

下面通过一个简单的例子介绍如何计算卷积和的参数量，这里定义如下网络：

import torch.nn as nn
class Net1(nn.Module):def __init__(self):super(Net1, self).__init__()self.conv1 = nn.Conv2d(1, 32, 5, padding=1)def forward(self, x):x = self.conv1(x)return x

该网络包括一个卷积层，输入通道数为1，输出通道数为32，卷积核大小为5×5，计算该层的参数量。
解释：因为输入通道数为1，因此卷积核大小可以表示为5×5×1，输出通道数为32，表明该层使用32个卷积核，同时每个卷积核有一个偏置值，因此参数量为：5×5×1×32+32=832。
通过代码验证可得：

from ptflops import get_model_complexity_infomodel = Net1()
ops, params = get_model_complexity_info(model, (1, 512, 512), as_strings=True,print_per_layer_stat=False, verbose=True)
params,5*5*1*32+32

运行结果：

这时可以看到，卷积操作的参数量核输入图像的尺寸大小无关，上述输入图像尺寸为1×512×512，如果使用全连接网络的话，那么此时输入层的结点个数为512×512=262144，如果隐含层结点个数为8，那么此时全连接网络的参数量为262144×8+8，之所以加8，是因为隐含层每个神经元都有一个偏置。
这是可以看到，卷积神经网络相对于全连接网络的优势，权值共享，参数量小。
为什么称权值共享呢？因为每个特征图的计算依赖于同一个卷积核。

2.2案例二

为了避免你还未理清如何计算参数量这里再举一个例子，网络结构如下：

class Net2(nn.Module):def __init__(self):super(Net2, self).__init__()self.conv1 = nn.Conv2d(8, 32, 3, padding=1)def forward(self, x):x = self.conv1(x)return x

该网络包括一个卷积层，输入通道数为8，输出通道数为32，卷积核大小为3×3，计算该层的参数量。
解释：因为输入通道数为8，因此卷积核大小可以表示为3×3×8，输出通道数为32，表明该层使用32个卷积核，同时每个卷积核有一个偏置值，因此参数量为：3×3×8×32+32=2336。
代码验证：

model = Net2()
ops2, params2 = get_model_complexity_info(model, (8, 256, 256), as_strings=True,print_per_layer_stat=False, verbose=True)
params2,3*3*8*32+32

运行结果：

3.奇怪的优化思想

在卷积这一块，有很多优化思想，来所谓的减少参数量，这里主要介绍两种主流思想。

3.1使用小核卷积替换大核卷积

该思想来源于VGG网络的设计思想，论文地址：VGG网络模型，众所周知，之所以使用大核卷积，是为了获得更大的感受野，捕获更大的局部依赖关系。
前提知识：使用两个3×3的卷积核的感受野和一个5×5的卷积核的感受野大小一致。
这里我们定义两个网络，一个使用小核卷积，另一个使用大核卷积，假设每个卷积操作前后图像的深度保持不变。
大核卷积网络结构：

import torch.nn as nn
class Net1(nn.Module):def __init__(self):super(Net1, self).__init__()self.conv1 = nn.Conv2d(32, 32, 5, padding=2)def forward(self, x):x = self.conv1(x)return x

参数量：

小核卷积网络结构：

class Net3(nn.Module):def __init__(self):super(Net3, self).__init__()self.conv1 = nn.Conv2d(32, 32, 3, padding=1)self.conv2 = nn.Conv2d(32, 32, 3, padding=1)self.relu = nn.ReLU()def forward(self, x):x = self.conv1(x)x = self.relu(x)x = self.conv2(x)x = self.relu(x)return x

参数量：

从结果来看，小核卷积参数量更小，但能够和大核卷积达到相同的感受野。这就是为什么越来越多的网络结构使用小核卷积替换大核卷积。

3.2卷积核1×1的应用

这里直接举两个例子来介绍：
未使用1×1的卷积核：

class Net4(nn.Module):def __init__(self):super(Net4, self).__init__()self.conv1 = nn.Conv2d(256, 512, 3, padding=1)def forward(self, x):x = self.conv1(x)return x

参数量：

使用1×1卷积核：

class Net5(nn.Module):def __init__(self):super(Net5, self).__init__()self.conv1 = nn.Conv2d(256, 32, 1)self.conv2 = nn.Conv2d(32, 512, 3, padding=1)def forward(self, x):x = self.conv1(x)x = self.conv2(x)return x

参数量：

从结果来看，使用1×1的卷积核减少通道数，能够在一定程度上减少参数量，但在减少参数量的同时，输入的信息量也随之减少，如果输入的信息是一个稀疏矩阵的话，那么该方法确实适合减少参数量。

4.输出图像尺寸的计算

前面所说，都是考虑的是卷积的参数量，接着讨论输出图像尺寸如何计算。
卷积主要分为三种，Full convolution、Same convolution、valid convolution，这里主要介绍用处较多的一种，即Same convolution

4.1Same convolution

主要是设置padding参数的值
网络结构：

class Net6(nn.Module):def __init__(self):super(Net6, self).__init__()self.conv2 = nn.Conv2d(32, 512, 3, padding='same')def forward(self, x):x = self.conv2(x)return x

运行测试：

import torch
model = Net6()
I=torch.randn(32,128,128)
model(I).shape

运行结果：

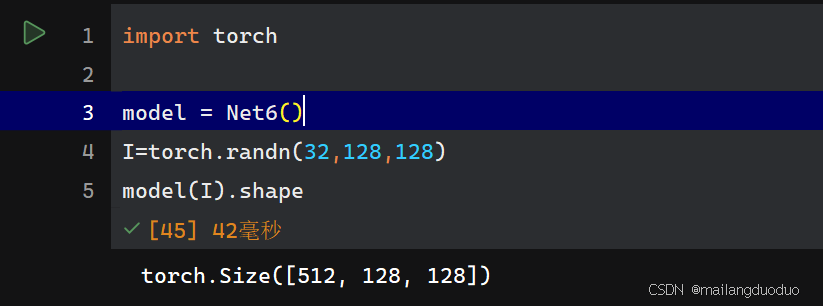
解释：输入图像的尺寸为32×128×128，通过网络结构可以看出，该层使用512个卷积核，因此输出通道数为512，因为padding参数设置的是same，输出会保持图像的尺寸大小。
有时并不将其设置为same，而是设置一个具体的值，这里只是因为设置了same，其自动计算了一个具体的值代入进去了而已。

4.2具体计算规则

输出图像的尺寸，不仅和填充列数有关，还和卷积核大小以及卷积步长有关。具体计算公式如下：
$$W_2=\frac{(W_1-F+2P)}{S}+1$$
$$H_2=\frac{(H_1-F+2P)}{S}+1$$
其中，$W_1、H_1$表示输入图像的尺寸大小，$W_2、H_2$表示输出图像的尺寸大小，F为卷积核尺寸，S为卷积步长，P为零填充数量。
下面举一个详细的例子说明。
网络结构为：

class Net7(nn.Module):def __init__(self):super(Net7, self).__init__()self.conv2 = nn.Conv2d(32, 512, 5, padding=1,stride=2)def forward(self, x):x = self.conv2(x)return x

输出结果：

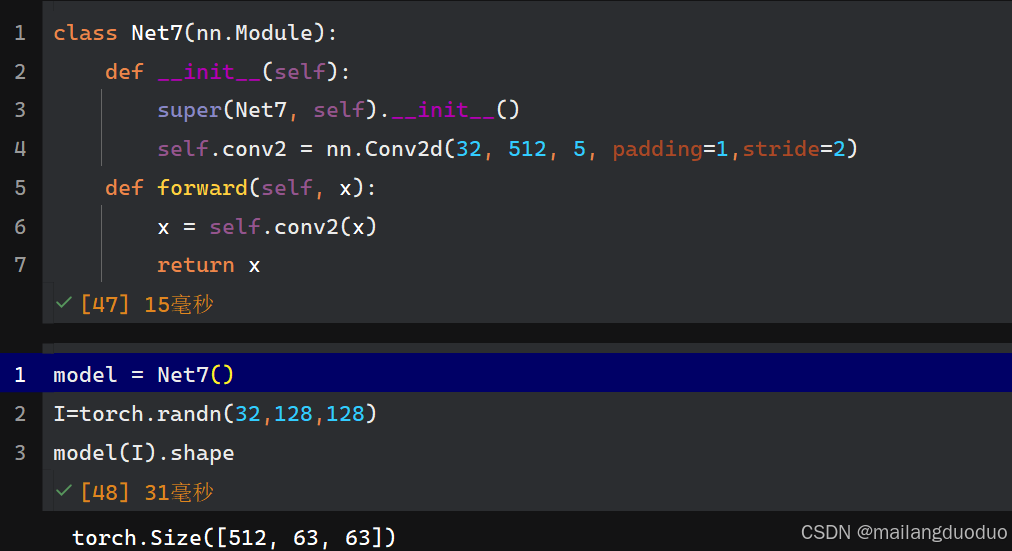
解释：根据公式计算即可，(128-5+2*1)/2+1=63，除法运算一律向下取整。输出通道数和卷积核个数512保持一致，因此输出形状为512×63×63。

4.3转置卷积

转置卷积（Transposed Convolution），又称反卷积（Deconvolution），具体计算方式也是卷积的逆运算。
由卷积计算公式为：
$$W_2=\frac{(W_1-F+2P)}{S}+1$$
$$H_2=\frac{(H_1-F+2P)}{S}+1$$
转置卷积，与其计算方式相反，相当于反函数的关系。
$$W_1=S\times (W_2-1)-2P+F$$
$$H_1=S\times (H_2-1)-2P+F$$
其中，$W_1、H_1$表示输出图像的尺寸大小，$W_2、H_2$表示输入图像的尺寸大小，F为卷积核尺寸，S为卷积步长，P为零填充数量。
下面举一个详细的例子说明。

class Net8(nn.Module):def __init__(self):super(Net8, self).__init__()# 转置卷积self.conv_transpose = nn.ConvTranspose2d(in_channels=32, out_channels=16, kernel_size=3, stride=2, padding=1)def forward(self, x):x = self.conv_transpose(x)return x

输出结果：

解释：根据公式计算即可，2*(128-1)-2*1+3，输出通道数和卷积核个数16保持一致，因此输出形状为16×255×255。

小结

通过本篇博客，相比你也能够计算卷积神经网络中图像尺寸如何变化的，快去找一个深层的网络试试看吧，看它的尺寸变化是否和你想的一样呢？可以试试本篇博客设计的网络模型——Unet语义分割模型