当前位置：首页 > news >正文

GESP 七级实操题

news 2025/9/17 15:19:24

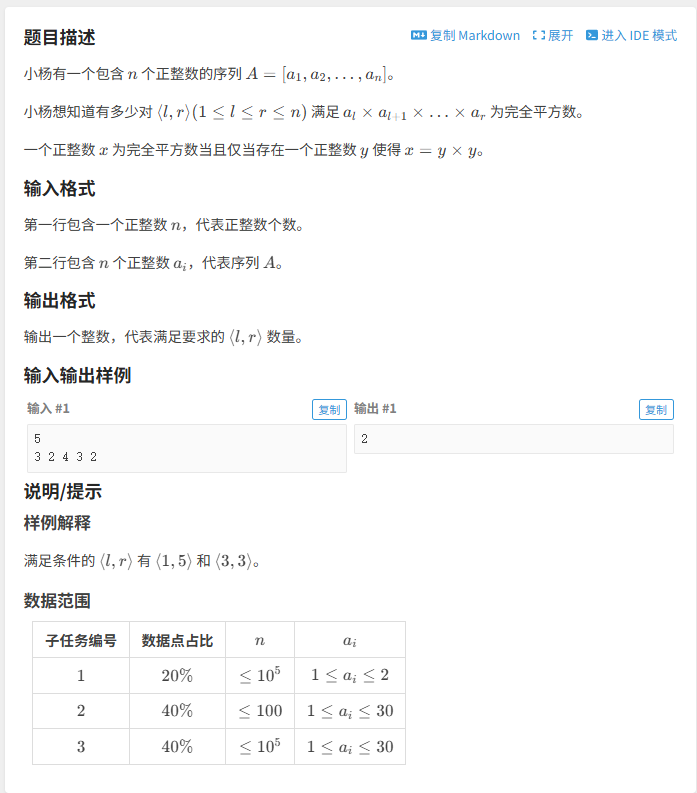
洛谷 P10724 [GESP202406 七级] 区间乘积

P10724 [GESP202406 七级] 区间乘积 - 洛谷

完全平方数定义：

若x是完全平方数，则x = y × y（y $\in$ N）。
若x是完全平方数，对x进行质因数分解，质因数的指数是偶数。

时间：O(n)求解，不能for循环嵌套。

方法一：用二进制位表示质数的情况（ai ≤ 30，30以内的质数有10个），考虑一个非完全平方数和多少相乘变成完全平方数。

#include <iostream>
#include <cmath>
using namespace std;typedef long long LL;const LL Maxn = 1e5 + 5;
const LL Maxp = 10;
const LL Maxa = 30 + 5;LL v_prime[Maxp] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29};
LL nums[(1 << Maxp) + 5], vct[Maxa];void getVct() {LL x = 0;for (LL i = 1; i <= 30; ++i) {x = i;for (LL j = 0; j < Maxp; ++j) {while (x % v_prime[j] == 0) {x /= v_prime[j];vct[i] ^= (1 << j);}}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);LL n, x, res = 0, prexor = 0;cin >> n;getVct();nums[0] = 1;for (LL i = 1; i <= n; ++i) {cin >> x;prexor ^= vct[x];res += nums[prexor];nums[prexor]++;;}cout << res;return 0;
}

洛谷 P11965 [GESP202503 七级] 等价消除

P11965 [GESP202503 七级] 等价消除 - 洛谷

代码如下：

// 2025.05.26 T1#include <iostream>
#include <string>
#include <unordered_map>
using namespace std;typedef long long LL;LL ump[(1 << 26) + 5];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);LL n;string str;cin >> n >> str;LL num = 0, res = 0;ump[0] = 1;for (LL j = 0; j < n; ++j) {num ^= (1 << ((LL) str[j] - 'a'));res += ump[num];++ump[num];}cout << res;return 0;
}

有26个字母，所以可用二进制表示每个字母的状态，题目中多个数据范围很大，一个数据范围很小，考虑二进制。

洛谷 P10287 [GESP样题七级] 最长不下降子序列

P10287 [GESP样题七级] 最长不下降子序列 - 洛谷

时间：O(n)求解，遍历一遍图就要求出结果。

转化成线性结构：

最长不降子序列一般在线性结构上求解，通过遍历，将有向无环图转换成线性结构。
考虑dfs，发现只有在指向节点x的节点的最长不降子序列的长度确定之后，才能确定到x的最长不下降子序列的长度，否则会有后效性。
满足拓扑排序的前提，将图通过拓扑排序，转换成线性结构，在线性结构上求解最长不降子序列，在拓扑排序的过程中，本身就形成了线性结构，那么边排序边求到当前点的最长不降子序列。

代码如下：

#include <iostream>
#include <queue>
#include <cmath>
using namespace std;typedef long long LL;const LL Maxn = 1e5 + 5;
const LL Maxm = 1e5 + 5;
const LL MVal = 10 + 5;vector<LL> grid[Maxn];
LL v_value[Maxn], Rdeg[Maxn], dp[Maxn][MVal];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);LL n, m, u, v;cin >> n >> m;for (LL i = 1; i <= n; ++i)  cin >> v_value[i];for (LL i = 1; i <= m; ++i) {cin >> u >> v;grid[u].emplace_back(v);++Rdeg[v];}queue<LL> que;for (LL i = 1; i <= n; ++i) {if (Rdeg[i] == 0)  que.push(i);dp[i][v_value[i]] = 1;}LL cur = 0;while (!que.empty()) {cur = que.front(); que.pop();for (auto v : grid[cur]) {if ((--Rdeg[v]) == 0)  que.push(v);for (LL i = 1; i <= 10; ++i) {if (i <= v_value[v])  dp[v][v_value[v]] = max(dp[v][v_value[v]], dp[cur][i] + 1);dp[v][i] = max(dp[v][i], dp[cur][i]);}}}LL res = 0;for (LL i = 1; i <= n; ++i) {for (LL j = 1; j <= 10; ++j)res = max(res, dp[i][j]);}cout << res;return 0;
}

总结：