【CF】Day80——Codeforces Round 872 (Div. 2) C⭐D (思维 + 模拟 | 树 + 思维 + 组合数学 + 分数取模)
C. LuoTianyi and the Show
题目:

 思路:
思路:
简单思维题
题目告诉我们一堆步骤,但是其实很简单就能看出来一些端倪
首先我们一定可以放入所有的 xi > 0 的点,且在此基础上我们可以选择放入全部的 x = -1 的点和 x = -2 的点
证明:以左边举例,假设前 i - 1 个数都填上了,如果当前点 i 没有对应的 x = i 点,那么就消耗 x = -1 的点,否则消耗 x = i 的点
因此这是两种答案,那么如果两个都放呢?
由于两个都要放,那么显然就要以一个点做分界点,然后将所有的 -1 放入左边,所有的 -2 放入右边,为什么呢?由于 -1 一定是放在最左边的左边,那么肯定是一直往左走,右边同理,类似于洪水一般,最终我们一定能将所有的 -1 用掉(如果 -1 的数量大于空位,那么就要取 min)
因此我们可以使用前缀和先把所有 x > 0 的位置标成1求前缀和,然后枚举分界点算奉献即可
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"void solve()
{int n, m;cin >> n >> m;vector<int> a(n);int one = 0,two = 0;vector<int> x(m + 1,0);int res = 0;for (int i = 0; i < n; i++){cin >> a[i];if (a[i] == -1){one++;}else if(a[i] == -2){two++;}else{if (x[a[i]] == 0){res++;}x[a[i]]=1;}}int ans = res;vector<int> sum(m + 1, 0);for (int i = 1; i <= m; i++){sum[i] = sum[i - 1];sum[i] += x[i];}for (int i = 1; i <= m; i++){if (x[i]){int left = min(sum[i-1] + one,i-1);int right = min(sum[m] - sum[i] + two, m - i);int temp = 1 + left + right;ans = max(ans, temp);}}cout << max({ ans,min(res + one,m),min(res + two,m) }) << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(false);int t = 1;cin >> t;while (t--){solve();}return 0;
}D. LuoTianyi and the Floating Islands
题目:

 思路:
思路:
结论题,还是主考数学
这一题其实相当于考了一个中位数定理,我们来分析一下
如果是奇数,那么一定是只有一个点最小,即中间的点
如果是偶数,那么就一定是左边有 k/2 个点,右边也有 k/2 个点
那么对于奇数情况的期望显然是 1,因为每一种选择只有一种好岛,所有肯定是 1
而偶数情况怎么算呢?如果我们直接算边的话显然有点麻烦,那我们就转化为算边好了
我们定义一个 pi 为节点 i 和其父节点都是好点的期望,那么既然 i 和其父节点都满足了都是好点,那么左右两边一定都有 k/2 个点,所以对于这条边,我们有 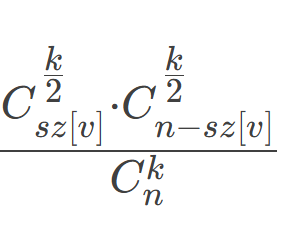
这么多的奉献,那么最后的答案就是累加上所有的边的奉献即可。。。吗?
实则不然,由于 pi 的定义是和其父节点有关,当其父节点不是好点时,那么其奉献就是 0,但实际上每一种情况都一定会有一种可能,所以结果是

因为当多个好节点连在一起时才会形成路径,此时 pi 才有奉献,否则一定没有
或者这样说,由于我们算边的贡献时只有边,而点的数量是边数+1,所以每次算的时候都会少1(即少了单独的情况),那么根据数学可知,由于每个结果都少了 1,那么 EX ~ (X, P) 就会变成EX‘ = EX + 1
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"const int MOD = 1e9 + 7;int n, k;
int fac[200005];
int infac[200005];
int ksm(int a, int b)
{a %= MOD;int res = 1;while (b) {if (b & 1)res = res * a % MOD;a = a * a % MOD;b >>= 1;}return res;
}
void Init()
{fac[0] = infac[0] = 1;for (int i = 1; i <= n; i++){fac[i] = fac[i - 1] * i % MOD;}infac[n] = ksm(fac[n], MOD - 2);for (int i = n-1; i >= 1; i--){infac[i] = infac[i + 1] * (i + 1) % MOD;}
}int C(int a, int b)
{return (a < b || b < 0) ? 0 : fac[a] * infac[b] % MOD * infac[a-b] % MOD;
}void solve()
{cin >> n >> k;vector<vector<int>> g(n + 1);for (int i = 0; i < n - 1; i++){int u, v;cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}if (k % 2){cout << "1\n";return;}int p = 0;vector<int> sonsize(n + 1, 0);auto dfs = [&](auto self, int fa, int se) -> void {sonsize[se] = 1;for (auto& son : g[se]){if (son == fa) continue;self(self, se, son);sonsize[se] += sonsize[son];p = (p + C(sonsize[son], k / 2) * C(n - sonsize[son], k / 2) % MOD) % MOD;}};Init();dfs(dfs, 0, 1);int q = C(n, k);//最后加 1 是因为我们算的是边的期望,但是题目要的是点cout << ((p % MOD * ksm(q, MOD - 2)) % MOD + 1) % MOD << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(false);int t = 1;while (t--){solve();}return 0;
}