材料力学速通

材料力学速通

公式速通

拉伸

正应力：

$$\sigma =\frac{F_N}{A}$$

拉伸变形：

$$\Delta l=\frac{F_N\text{d}x}{EA}$$

剪切

$$\tau =\frac{F_s}{A}$$

挤压

$${\sigma }_{bs}=\frac{F_{bs}}{A_{bs}}$$

扭转

等直圆轴在某截面内$\rho$处的切应力公式：

$$\tau =\frac{T\rho }{T_p}$$

其中：

$T$为扭矩，$\rho$为截面内某一点，$T_p={\int }_A{\rho }^2\text{A}$

扭转变形的相对转角公式：

$$\text{d}\phi =\frac{T}{G{I}_p}\text{d}x$$

弯曲

载荷集度、剪力与弯矩之间的关系：

$$q(x)=\frac{\text{d}{F}_s(x)}{\text{d}x}$$

$$F_s(x)=\frac{\text{d}M(x)}{\text{d}x}$$

1. 无载荷作用，剪力变化率为$0$，即剪力图为水平直线，弯矩图为直线，剪力为正则弯矩图为倾斜向上的直线，反之为倾斜向下的直线；

2. 有均布载荷作用，剪力变化率不变，即剪力图为有斜率的直线，当剪力有变号零点时，剪力图出现极值点，反之保持凹凸性不变的无极值点的二次函数图像；

3. 集中力作用，导致剪力突变，突变量与集中力大小相等，方向相同，弯矩图出现"尖点"；

4. 集中力偶作用，导致弯矩突变，突变量与集中力偶大小相等，方向相同。

5. 弯矩的极值通常发生在剪力为零的点，或集中力作用且两侧剪力变号的点。

弯曲应力的计算：

纯弯曲正应力
$$\sigma =\frac{My}{I_z}$$

横力弯曲切应力

$$\tau =\frac{F_s{S}_z^{\ast }}{I_{z}b}$$

其中$y$代表距离中性层的位置，$b$为截面宽度，$S_z^{\ast }$为位置$y$以下部分对中性轴的静矩。

弯曲变形下：

$$w^{\prime \prime }=\frac{M(x)}{EI}$$

挠曲线的近似微分方程需要满足边界条件与连续性条件。即对于边界约束。若限制挠度方向位移，其挠度就为$0$，若边界有约束力偶，则转角为$0$.

莫尔圆

$${\left({\sigma }_{\alpha }-\frac{{\sigma }_x+{\sigma }_y}{2}\right)}^2+{\tau }_{\alpha }^2={\tau }_{xy}^2+{\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2$$

强度校核理论

1. 第一强度理论：
   $${\sigma }_1\le [\sigma ]$$
2. 第二强度理论:
   $${\sigma }_1-\mu ({\sigma }_2+{\sigma }_3)\le [\sigma ]$$
3. 第三强度理论:

$${\sigma }_1-{\sigma }_3\le [\sigma ]$$

4. 第四强度理论

$$\sqrt{\frac{1}{2}\sum _{cyc}[{\sigma }_i-{\sigma }_j{]}^2}\le [\sigma ]$$

组合变形

在线性小变形条件下，复杂变形可由基本变形类型叠加形成。

1. 拉伸或压缩与弯曲组合：当$EI$比较大时，可以忽略轴向力的引起的弯矩。
2. 偏心压缩时的中性轴方程：

$$\frac{y_F{y}_0}{i_z^2}+\frac{z_F{z}_0}{i_y^2}=-1$$

3. 弯扭组合圆轴截面的危险点为二向应力状态，边缘点：
   $$\sigma =\frac{M}{W_z}$$
   $$\tau =\frac{T}{W_t}$$

压杆稳定

临界压力公式：
$$F_{cr}=\frac{{\pi }^{2}EI}{(\mu l{)}^2}$$

柔度定义为：
$$\lambda =\frac{\mu l}{i}$$
只有当柔度大于或者等于$\pi \sqrt{\frac{E}{{\sigma }_p}}$,欧拉拉公式适用。

例题

一

求最大弯矩有最小值时候的铰链$C$位置。

解

对$AC$和$CD$刚体进行分析：

$$F_A=q(l-x)+\frac{1}{2}qx$$
$$M_A=\frac{1}{2}qx(l-x)+\frac{1}{2}q(l-x{)}^2$$
$$F_B=\frac{1}{2}qx$$
$$F_C=\pm \frac{1}{2}qx$$

作剪力图（示例）：

显然，在$C$处的弯矩为0，则：

$A$处的弯矩负向最大，零点处的弯矩正向最大：

$$\begin{array}{rl}|M_A|& =\frac{1}{2}qx(l-x)+\frac{1}{2}q(l-x{)}^2\\ |M_D|& =\frac{1}{8}q{x}^2\end{array}$$

令$|M_A|=|M_D|$ ，即：

$$\frac{1}{2}qx(l-x)+\frac{1}{2}q(l-x{)}^2=\frac{1}{8}q{x}^2$$

得到：

$$x=(2\sqrt{2}-2)l$$

二

简支梁受均布载荷作用，求最底层纤维伸长量。

解

弯矩：

$$M(x)=\frac{q}{2}x(l-x)$$

正应力：

$$\sigma =\frac{\frac{q}{2}x(l-x)}{W_z}$$

总伸长量：

$$\Delta l={\int }_0^l\frac{\frac{q}{2}x(l-x)}{E{W}_z}\text{d}x$$

三

求解下图中$A$截面的转角与$B$截面的挠度。

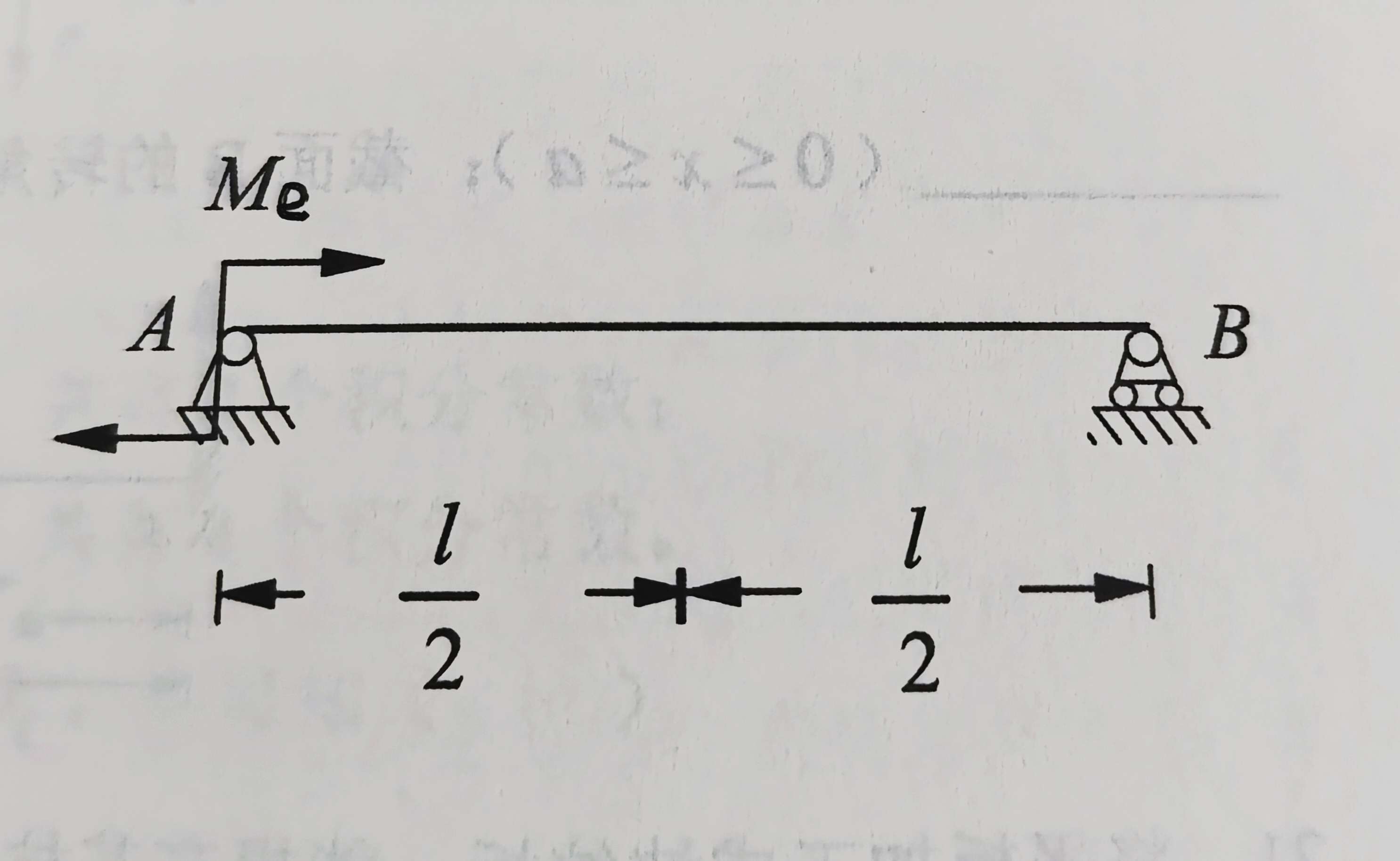
解

对于第一个得到其挠曲线近似微分方程为：

$$w^{\prime \prime }(x)=\frac{M_e\left(1-\frac{x}{l}\right)}{EI}$$

附加边界条件：

$$\begin{array}{rl}& w{|}_{x=0}=0\\ & w{|}_{x=l}=0\end{array}$$
对于第二个：
对于 CD 段$(0\le x\le l)$，挠曲线微分方程为：
$$EI{w}_1^{\prime \prime }=M_1(x)=-\frac{P}{2}x$$

对于 DA(B)段$(l\le x\le \frac{3l}{2})$，挠曲线微分方程为：
$$EI{w}_2^{\prime \prime }=M_2(x)=P\left(x-\frac{3l}{2}\right)$$
附加边界条件与连续性条件
$$\begin{array}{rl}& w{|}_{x=0}=0\\ & w{|}_{x=l，1}=w{|}_{x=l，2}=0\\ & \theta {|}_{x=l，1}=\theta {|}_{x=l，2}\end{array}$$